Contents
円の極と極線に関する性質

ヒロ
円の極と極線に関する有名な性質を知っておこう。
次の図のように,極Pを通る直線と円 $C$ の2つの交点をQ,Rとし,極線ABとの交点をSとする。
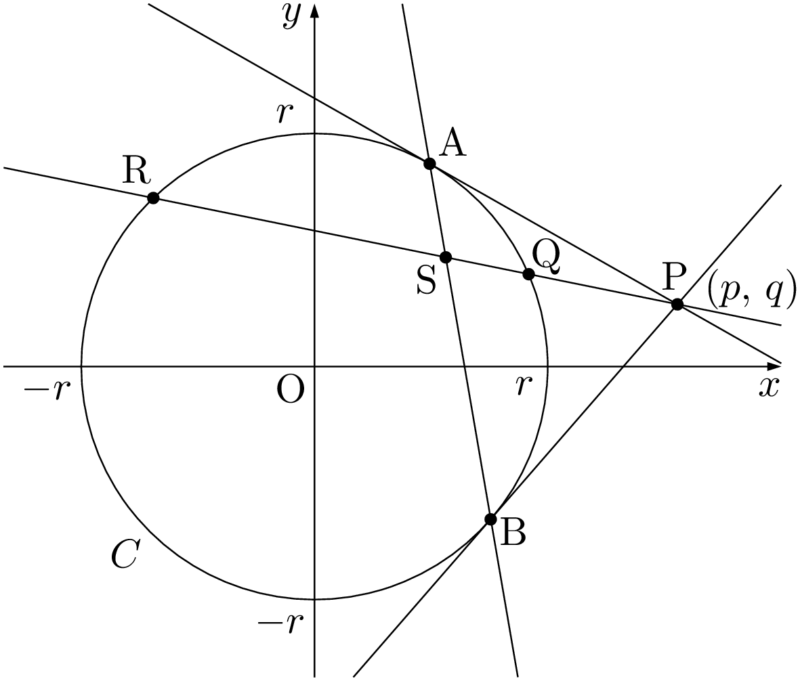
このとき,線分PSに対して,点Qは内分点で点Rは外分点となる。内分比は $\text{PQ}:\text{QS}$ であり,外分比は $\text{PR}:\text{RS}$ であるが,「内分比と外分比が等しい」という性質がある。つまり
\begin{align*}
\text{PQ}:\text{QS}=\text{PR}:\text{RS}
\end{align*}
が成り立つ。ここで\text{PQ}:\text{QS}=\text{PR}:\text{RS}
\end{align*}
\begin{align*}
\text{PQ}=a,~\text{PR}=b,~\text{PS}=c
\end{align*}
とおくと\text{PQ}=a,~\text{PR}=b,~\text{PS}=c
\end{align*}
\begin{align*}
&a:(c-a)=b:(b-c) \\[4pt]
&a(b-c)=b(c-a) \\[4pt]
&ab-ac=bc-ab \\[4pt]
&ac+bc=2ab
\end{align*}
両辺を $abc$ で割ると&a:(c-a)=b:(b-c) \\[4pt]
&a(b-c)=b(c-a) \\[4pt]
&ab-ac=bc-ab \\[4pt]
&ac+bc=2ab
\end{align*}
\begin{align*}
\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{2}{c}
\end{align*}
となる。\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{2}{c}
\end{align*}
この結果は,3つの数 $\dfrac{1}{a},~\dfrac{1}{c},~\dfrac{1}{b}$ が等差数列をなすことを示している。
さらに言い換えると $a,~c,~b$ が調和数列をなすと言える。
このことから,4点P,Q,S,Rを調和点列といい,2点Q,Rは線分PSを調和分割するという。

ヒロ
この「円の極と極線に関する性質」を扱った問題が2018年の島根大で出題されている。
円の極と極線に関する問題【島根大】
2018年 島根大円 $C:x^2+y^2=25$ と点P$(7,~1)$ がある。点Pから円 $C$ に二つの接線を引き,それらの接点をA,Bとする。また,点Pから円 $C$ と2点で交わる直線 $l:x=v_1t+7$,$y=v_2t+1$ を引く。ただし,$t$ は変数で $v_1<0$,${v_1}^2+{v_2}^2=1$ である。$l$ と $C$ との交点をQ,Rとし,$l$ と直線ABとの交点をSとする。このとき,次の問いに答えよ。
(1) 直線ABの方程式を求めよ。
(2) PSの長さを $c$ とするとき,$c$ を $v_1$ と $v_2$ を用いて表せ。
(3) PQ,PRの長さをそれぞれ $a,~b$ とするとき,次が成り立つことを示せ。
(1) 直線ABの方程式を求めよ。
(2) PSの長さを $c$ とするとき,$c$ を $v_1$ と $v_2$ を用いて表せ。
(3) PQ,PRの長さをそれぞれ $a,~b$ とするとき,次が成り立つことを示せ。
\begin{align*}
\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{2}{c}
\end{align*}
\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{2}{c}
\end{align*}

ヒロ
「円の極と極線」を知っている人にとっては,この問題は極や極線に関する問題だなと分かる。

ヒロ
しかし,知識だけあっても,問題を解くことができなければ何の意味もない。

ヒロ
知識もあって,問題を解けるようにすると完璧だろう。
【(1)の考え方と解答】
円 $C$ 上の点 $(p,~q)$ における接線の方程式は
よって,求める直線ABの方程式は $7x+y=25$
円 $C$ 上の点 $(p,~q)$ における接線の方程式は
\begin{align*}
px+qy=25
\end{align*}
と表せる。これが点P$(7,~1)$ を通るときpx+qy=25
\end{align*}
\begin{align*}
7p+q=25
\end{align*}
が成り立つ。したがって,2つの接点A,Bの座標をそれぞれ $(p_1,~q_1)$,$(p_2,~q_2)$ とすると7p+q=25
\end{align*}
\begin{align*}
7p_1+q_1=25,~7p_2+q_2=25
\end{align*}
が成り立つ。これは2点A,Bが直線 $7x+y=25$ 上にあることを示している。7p_1+q_1=25,~7p_2+q_2=25
\end{align*}
よって,求める直線ABの方程式は $7x+y=25$
(2) PSの長さを $c$ とするとき,$c$ を $v_1$ と $v_2$ を用いて表せ。
【(2)の考え方と解答】
文章だけを読んでも,どのような状態か分かりにくいので図を描くと,次のようになる。
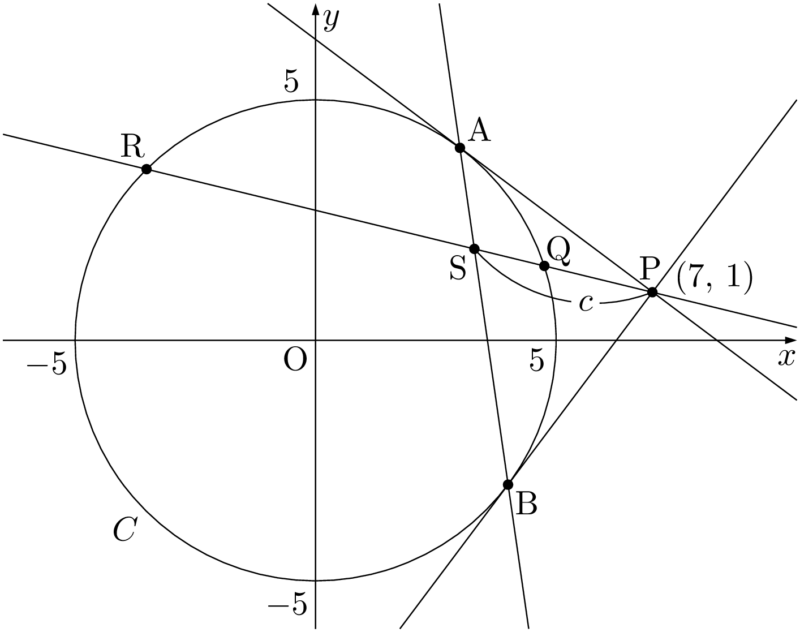
$c$ の値を求めるためには,2点P,Sの座標が必要である。点Pの座標は $(7,~1)$ と与えられているから,点Sの座標を求めればよい。点Sは直線 $l$ 上にあることが分かっているから,S $(v_1t+7,~v_2t+1)$ とおける。このとき
よって,$\text{PS}=c=\abs{t}$
あとは,点Sになる $t$ の値を求めなければならない。さらに,その $t$ の符号を特定することができるなら絶対値も外せる。点Sが直線 $l$ と直線ABの交点であることを利用すれば,$t$ の値を求めることができそう。
S $(v_1t+7,~v_2t+1)$ は直線AB $7x+y=25$ 上にあるから
このように,解答の途中でどうすれば良いか分からなくなった場合は「まだ使ってない条件」に着目しよう。問題文を読むと,まだ使っていない条件に気付くだろう。
このことを踏まえて,次のように「解答」を書けば良い。
点Sの $x$ 座標は点Pの $x$ 座標の7より小さいから
$c=\abs{t}=t$ より
文章だけを読んでも,どのような状態か分かりにくいので図を描くと,次のようになる。

$c$ の値を求めるためには,2点P,Sの座標が必要である。点Pの座標は $(7,~1)$ と与えられているから,点Sの座標を求めればよい。点Sは直線 $l$ 上にあることが分かっているから,S $(v_1t+7,~v_2t+1)$ とおける。このとき
\begin{align*}
\text{PS}^2&=(v_1t)^2+(v_2t)^2 \\[4pt]
&=({v_1}^2+{v_2}^2)t^2 \\[4pt]
&=t^2
\end{align*}
※問題文で与えられている「${v_1}^2+{v_2}^2=1$」を使っている。\text{PS}^2&=(v_1t)^2+(v_2t)^2 \\[4pt]
&=({v_1}^2+{v_2}^2)t^2 \\[4pt]
&=t^2
\end{align*}
よって,$\text{PS}=c=\abs{t}$
あとは,点Sになる $t$ の値を求めなければならない。さらに,その $t$ の符号を特定することができるなら絶対値も外せる。点Sが直線 $l$ と直線ABの交点であることを利用すれば,$t$ の値を求めることができそう。
S $(v_1t+7,~v_2t+1)$ は直線AB $7x+y=25$ 上にあるから
\begin{align*}
&7(v_1t+7)+(v_2t+1)=25 \\[4pt]
&(7v_1+v_2)t=-25~\cdots\cdots(\ast)
\end{align*}
$(\ast)$ の両辺を $7v_1+v_2$ で割れば $t$ を $v_1,~v_2$ で表すことができるが,0でないことを言っていないので,このまま進めるのは少しまずい気がする。&7(v_1t+7)+(v_2t+1)=25 \\[4pt]
&(7v_1+v_2)t=-25~\cdots\cdots(\ast)
\end{align*}
このように,解答の途中でどうすれば良いか分からなくなった場合は「まだ使ってない条件」に着目しよう。問題文を読むと,まだ使っていない条件に気付くだろう。
- 直線 $l$ が円 $C$ と異なる2点で交わる。
- $v_1<0$
直線と円が異なる2点で交わる条件を数式で考える場合は,点と直線の距離を用いることが多いが,今回は直線上の点が媒介変数で表されているため,円の方程式に代入して,得られた方程式をみたす $t$ が2つ存在する条件を考えることにする。
$x=v_1t+7,~y=v_2t+1$ を $C:x^2+y^2=25$ に代入すると
\begin{align*}
&(v_1t+7)^2+(v_2t+1)^2=25 \\[4pt]
&({v_1}^2+{v_2}^2)t^2+2(7v_1+v_2)t+25=0 \\[4pt]
&t^2+2(7v_1+v_2)t+25=0~\cdots\cdots①
\end{align*}
直線 $l$ と円 $C$ が異なる2点で交わるのは,方程式①が異なる2つの実数解をもつときだから,判別式を $D$ とすると&(v_1t+7)^2+(v_2t+1)^2=25 \\[4pt]
&({v_1}^2+{v_2}^2)t^2+2(7v_1+v_2)t+25=0 \\[4pt]
&t^2+2(7v_1+v_2)t+25=0~\cdots\cdots①
\end{align*}
\begin{align*}
&D/4=(7v_1+v_2)^2-25>0
\end{align*}
となる。これより,$7v_1+v_2\neq0$ であることが言える。$(\ast)$ の両辺を $7v_1+v_2$ で割ることができて&D/4=(7v_1+v_2)^2-25>0
\end{align*}
\begin{align*}
t=-\dfrac{25}{7v_1+v_2}
\end{align*}
あとは $v_1<0$ をどのように利用するかを考えるが,$v_1$ が使われているものに着目すると,点Sの $x$ 座標に着目することになるだろう。いま考えているのは $t$ の符号であるから,$v_1$ が負であることと $t$ の符号にどのような関係があるのかを考える。もし $t$ が正だとすると,$v_1t$ は負になるから t=-\dfrac{25}{7v_1+v_2}
\end{align*}
\begin{align*} v_1t+7<7 \end{align*}
となる。逆に $t$ が負だとすると,$v_1t$ は正になるから \begin{align*} v_1t+7>7
\end{align*}
となる。「7」との大小関係が得られるが,点Pの $x$ 座標が7であることを考えると,$t$ は正でなければならないことが分かる。\end{align*}
このことを踏まえて,次のように「解答」を書けば良い。
点Sの $x$ 座標は点Pの $x$ 座標の7より小さいから
\begin{align*}
&v_1t+7<7 \\[4pt] &v_1t<0 \end{align*}
である。$v_1<0$ であるから,$t>0$ である。&v_1t+7<7 \\[4pt] &v_1t<0 \end{align*}
$c=\abs{t}=t$ より
\begin{align*}
c=-\dfrac{25}{7v_1+v_2}
\end{align*}
c=-\dfrac{25}{7v_1+v_2}
\end{align*}
(3) PQ,PRの長さをそれぞれ $a,~b$ とするとき,次が成り立つことを示せ。
\begin{align*}
\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{2}{c}
\end{align*}
【(3)の考え方と解答】
PQやPRの長さが示すべき等式に現れているが,$\text{PS}^2$ を計算したときに $\text{PS}^2=t^2$ となったことを覚えていると見通しが良くなるだろう。点Pより左側にある直線 $l$ 上の点に対応する $t$ の符号は正であるから
したがって,2点Q,Rに対応する $t$ の値をそれぞれ $\alpha,~\beta$ とすると
PQやPRの長さが示すべき等式に現れているが,$\text{PS}^2$ を計算したときに $\text{PS}^2=t^2$ となったことを覚えていると見通しが良くなるだろう。点Pより左側にある直線 $l$ 上の点に対応する $t$ の符号は正であるから
\begin{align*}
\text{PS}=\abs{t}=t
\end{align*}
となる。これは,$t$ の値を定めると,その値に応じて直線 $l$ 上の点が1つ定まり,点Pからの距離がその点に対応する $t$ の値と等しいことを示している。\text{PS}=\abs{t}=t
\end{align*}
したがって,2点Q,Rに対応する $t$ の値をそれぞれ $\alpha,~\beta$ とすると
\begin{align*}
a=\text{PQ}=\alpha,~b=\text{PR}=\beta~\cdots\cdots②
\end{align*}
となる。また,2点Q,Rに対応する $t$ の値は,方程式①,つまりa=\text{PQ}=\alpha,~b=\text{PR}=\beta~\cdots\cdots②
\end{align*}
\begin{align*}
t^2+2(7v_1+v_2)t+25=0
\end{align*}
の2解である。$a,~b,~c$ の間に成り立つ関係式を証明したいことと,$c=-\dfrac{25}{7v_1+v_2}$ であることを考えると,①の $t$ の係数と定数項が関わっていることが分かる。これは「解と係数の関係を利用せよ」と言われているようなものである。実際に,解と係数の関係よりt^2+2(7v_1+v_2)t+25=0
\end{align*}
\begin{align*}
\alpha+\beta=-2(7v_1+v_2),~\alpha\beta=25~\cdots\cdots③
\end{align*}
が成り立つ。②,③より\alpha+\beta=-2(7v_1+v_2),~\alpha\beta=25~\cdots\cdots③
\end{align*}
\begin{align*}
a+b=-2(7v_1+v_2),~ab=25
\end{align*}
となるから,$c=-\dfrac{25}{7v_1+v_2}$ よりa+b=-2(7v_1+v_2),~ab=25
\end{align*}
\begin{align*}
&\dfrac{c}{2}=\dfrac{25}{-2(7v_1+v_2)} \\[4pt]
&\dfrac{c}{2}=\dfrac{ab}{a+b}
\end{align*}
$a,~b,~c$ はすべて正であるから&\dfrac{c}{2}=\dfrac{25}{-2(7v_1+v_2)} \\[4pt]
&\dfrac{c}{2}=\dfrac{ab}{a+b}
\end{align*}
\begin{align*}
&\dfrac{a+b}{ab}=\dfrac{2}{c} \\[4pt]
&\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{2}{c}
\end{align*}
&\dfrac{a+b}{ab}=\dfrac{2}{c} \\[4pt]
&\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{2}{c}
\end{align*}


















