ここでは円の極と極線について説明します。
曲線ではなく「極線」です。
極線という単語を知らなくても特に問題はない気がしますが,その求め方については知っておいた方が良いでしょう。
Contents
円の極と極線

ヒロ
次の例題を用いて,円の極と極線について説明する。
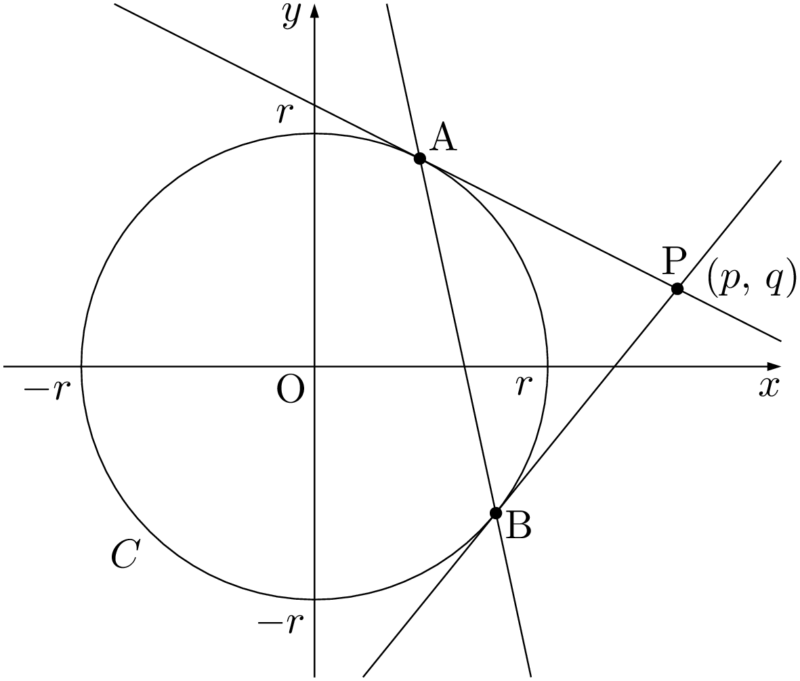
例題円 $C:x^2+y^2=r^2$ に円 $C$ の外部の点P $(p,~q)$ から引いた2本の接線の接点をA,Bとするとき,直線ABの方程式を求めよ。
【考え方と解答】
問題文通り「点Pから円 $C$ に接線を引く」と考えない方が良い。つまり,点Pを通る直線を $y=m(x-p)+q$ のようにおいて,この直線が円 $C$ に接する条件を考えるのは得策ではない。$p=r$ のときは接線が $y$ 軸と平行になるが,これが表せないのと,そもそも面倒である。一般的には「円 $C$ 上の点における接線が点Pを通る」と考えると楽になる。
円 $C$ 上の点 $(a,~b)$ における接線の方程式は
問題文通り「点Pから円 $C$ に接線を引く」と考えない方が良い。つまり,点Pを通る直線を $y=m(x-p)+q$ のようにおいて,この直線が円 $C$ に接する条件を考えるのは得策ではない。$p=r$ のときは接線が $y$ 軸と平行になるが,これが表せないのと,そもそも面倒である。一般的には「円 $C$ 上の点における接線が点Pを通る」と考えると楽になる。

円 $C$ 上の点 $(a,~b)$ における接線の方程式は
\begin{align*}
ax+by=r^2
\end{align*}
である。これが点P $(p,~q)$ を通るときax+by=r^2
\end{align*}
\begin{align*}
ap+bq=r^2
\end{align*}
が成り立つ。2点A,Bの座標をそれぞれA$(a_1,~b_1)$,B$(a_2,~b_2)$ とおくとap+bq=r^2
\end{align*}
\begin{align*}
a_1p+b_1q=r^2,~a_2p+b_2q=r^2
\end{align*}
が成り立つ。この2本の等式の見方が重要となる。上の2本の等式は,$p,~q$ の係数が異なり,右辺が等しいことに着目すると「$px+qy=r^2$ に $(x,~y)=(a_1,~b_1),~(a_2,~b_2)$ を代入したもの」と見ることができる。つまり,2点A,Bが直線 $px+qy=r^2$ 上にあることを示している。言い換えると,直線ABの方程式が $px+qy=r^2$ ということである。a_1p+b_1q=r^2,~a_2p+b_2q=r^2
\end{align*}

ヒロ
上で説明した「等式の捉え方」は有名なので,必ずできるようにしよう。

ヒロ
また,直線ABを点Pの極線といい,点Pを極という。


















