Contents
2018年 東洋大
2018年 東洋大$0\leqq\theta<2\pi$ のとき,$\cos^4\theta=\sin^4\theta$ を満たす $\theta$ は $\myhako$ 個ある。
【考え方と解答】
因数分解して解を求める方法で解の個数を調べよう。
与えられた方程式より
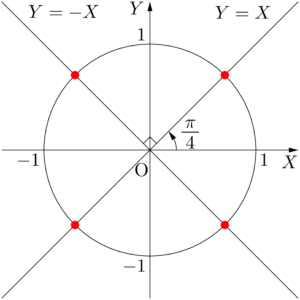
よって,条件を満たす $(X,~Y)$ は上図の4点存在するから,$\theta$ は4個ある。
因数分解して解を求める方法で解の個数を調べよう。
与えられた方程式より
\begin{align*} &\sin^4\theta-\cos^4\theta=0 \\[4pt] &(\sin^2\theta+\cos^2\theta)(\sin^2\theta-\cos^2\theta)=0 \\[4pt] &(\sin\theta+\cos\theta)(\sin\theta-\cos\theta)=0 \\[4pt] &\sin\theta=\pm\cos\theta \end{align*}
$\sin\theta=Y$,$\cos\theta=X$ とおくと,$(X,~Y)$ は直線 $Y=\pm X$ と円 $X^2+Y^2=1$ の共有点である。
よって,条件を満たす $(X,~Y)$ は上図の4点存在するから,$\theta$ は4個ある。
2016年 国士舘大
2016年 国士舘大$a$ を定数とする。$x$ に関する方程式
(1) この方程式が少なくとも1つの解をもつような定数 $a$ の値の範囲は $\dfrac{\myBox{ア}}{\myBox{イウ}}\leqq a\leqq\dfrac{\myBox{エ}}{\myBox{オ}}$ である。
(2) この方程式がちょうど8個の解をもつような定数 $a$ の値の範囲は $\dfrac{\myBox{カ}}{\myBox{キク}}<a<\dfrac{\myBox{ケ}}{\myBox{コ}}$ である。
(3) この方程式がちょうど6個の解をもつような定数 $a$ の値は $a=\dfrac{\myBox{サ}}{\myBox{シ}}$ である。
\begin{align*}
\sin^2x+\dfrac{1}{2}\abs{\cos x}+a-\dfrac{9}{8}=0
\end{align*}
について,次の問に答えよ。ただし,$0\leqq x<2\pi$ とする。\sin^2x+\dfrac{1}{2}\abs{\cos x}+a-\dfrac{9}{8}=0
\end{align*}
(1) この方程式が少なくとも1つの解をもつような定数 $a$ の値の範囲は $\dfrac{\myBox{ア}}{\myBox{イウ}}\leqq a\leqq\dfrac{\myBox{エ}}{\myBox{オ}}$ である。
(2) この方程式がちょうど8個の解をもつような定数 $a$ の値の範囲は $\dfrac{\myBox{カ}}{\myBox{キク}}<a<\dfrac{\myBox{ケ}}{\myBox{コ}}$ である。
(3) この方程式がちょうど6個の解をもつような定数 $a$ の値は $a=\dfrac{\myBox{サ}}{\myBox{シ}}$ である。
【(1)の考え方と解答】
$\cos x=t$ とおくと,$0\leqq x<2\pi$ のとき,$-1\leqq t\leqq1$ である。
与えられた方程式を①とすると,
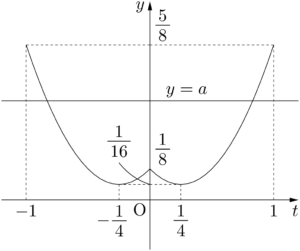
グラフより,求める $a$ の値の範囲は $\dfrac{1}{16}\leqq a\leqq\dfrac{5}{8}$
$\cos x=t$ とおくと,$0\leqq x<2\pi$ のとき,$-1\leqq t\leqq1$ である。
与えられた方程式を①とすると,
\begin{align*} &(1-t^2)+\dfrac{1}{2}\abs{t}+a-\dfrac{9}{8}=0 \\[4pt] &a=t^2-\dfrac{1}{2}\abs{t}+\dfrac{1}{8} \end{align*}
$f(t)=t^2-\dfrac{1}{2}\abs{t}+\dfrac{1}{8}$ とおく。 $t-1\leqq t\leqq0$ のとき \begin{align*} f(t)&=t^2+\dfrac{1}{2}t+\dfrac{1}{8} \\[4pt] &=\left(t+\dfrac{1}{4}\right)^2+\dfrac{1}{16} \end{align*}
$0\leqq t\leqq1$ のとき \begin{align*} f(t)&=t^2-\dfrac{1}{2}t+\dfrac{1}{8} \\[4pt] &=\left(t-\dfrac{1}{4}\right)^2+\dfrac{1}{16} \end{align*}
方程式①が少なくとも1つの解をもつのは,$y=f(t)$ のグラフと $y=a$ のグラフが $-1\leqq t\leqq1$ の範囲で共有点をもつときである。
グラフより,求める $a$ の値の範囲は $\dfrac{1}{16}\leqq a\leqq\dfrac{5}{8}$
(2) この方程式がちょうど8個の解をもつような定数 $a$ の値の範囲は $\dfrac{\myBox{カ}}{\myBox{キク}}<a<\dfrac{\myBox{ケ}}{\myBox{コ}}$ である。
【(2)の考え方と解答】
$\cos x=t~(0\leqq x<2\pi)$ の解 $x$ の個数は次のようになっている。
$-1<t<1$ のとき,$x$ は2個
$t=-1,~1$ のとき,$x$ は1個
$t<-1,~1<t$ のとき,$x$ はない
$y=f(t)$ のグラフと $y=a$ のグラフの共有点の個数を $k$ とすると,$k=0,~2,~3,~4$ のいずれかであるから,方程式①がちょうど8個の解をもつのは,$k=4$ のときである。
したがって,求める $a$ の値の範囲は $\dfrac{1}{16}<a<\dfrac{1}{8}$
$\cos x=t~(0\leqq x<2\pi)$ の解 $x$ の個数は次のようになっている。
$-1<t<1$ のとき,$x$ は2個
$t=-1,~1$ のとき,$x$ は1個
$t<-1,~1<t$ のとき,$x$ はない
$y=f(t)$ のグラフと $y=a$ のグラフの共有点の個数を $k$ とすると,$k=0,~2,~3,~4$ のいずれかであるから,方程式①がちょうど8個の解をもつのは,$k=4$ のときである。
したがって,求める $a$ の値の範囲は $\dfrac{1}{16}<a<\dfrac{1}{8}$
(3) この方程式がちょうど6個の解をもつような定数 $a$ の値は $a=\dfrac{\myBox{サ}}{\myBox{シ}}$ である。
【(3)の考え方と解答】
方程式①がちょうど6個の解をもつのは,$k=3$ のときであるから,グラフより求める $a$ の値は $a=\dfrac{1}{8}$
方程式①がちょうど6個の解をもつのは,$k=3$ のときであるから,グラフより求める $a$ の値は $a=\dfrac{1}{8}$


















