Contents
2直線の交点の軌跡【熊本大】
2019年 熊本大座標平面上の直線 $l$ を $y=ax-a-2$,直線 $m$ を $y=bx+3b$ とおく。直線 $l$ と直線 $m$ は互いに直交しながら座標平面上を動くとする。ただし,$a,~b$ は $l$ と $m$ の条件を保ちながら実数値をとって変化するものとする。直線 $l$ と直線 $m$ の交点Pの軌跡を求めよ。
【考え方と解答】
2直線 $l,~m$ が直交しているから,
以上のことから,2直線 $l,~m$ の交点Pの軌跡は,2点A,Bを直径の両端とする円となる。ただし,2点 $(1,~0)$,$(-3,~-2)$ を除く。
線分ABの中点の座標は $(-1,~-1)$ であり,
2直線 $l,~m$ が直交しているから,
\begin{align*}
ab=-1~\cdots\cdots①
\end{align*}
が成り立つ。$y=ax-a-2$ を変形するとab=-1~\cdots\cdots①
\end{align*}
\begin{align*}
y=a(x-1)-2
\end{align*}
となるから,直線 $l$ は $a$ の値にかかわらず,点A$(1,~-2)$ を通る。ただし,直線 $x=1$ と一致することはない。また,$y=bx+3b$ を変形するとy=a(x-1)-2
\end{align*}
\begin{align*}
y=b(x+3)
\end{align*}
となるから,直線 $m$ は $b$ の値にかかわらず,点B$(-3,~0)$ を通る。ただし,直線 $x=-3$ と一致することはない。y=b(x+3)
\end{align*}
以上のことから,2直線 $l,~m$ の交点Pの軌跡は,2点A,Bを直径の両端とする円となる。ただし,2点 $(1,~0)$,$(-3,~-2)$ を除く。
線分ABの中点の座標は $(-1,~-1)$ であり,
\begin{align*}
\text{AB}&=\sqrt{(1+3)^2+(0+2)^2} \\[4pt]
&=\sqrt{20}=2\sqrt{5}
\end{align*}
であるから,点Pの軌跡は,中心 $(-1,~-1)$,半径 $\sqrt{5}$ の円である。ただし,2点 $(1,~0)$,$(-3,~-2)$ を除く。\text{AB}&=\sqrt{(1+3)^2+(0+2)^2} \\[4pt]
&=\sqrt{20}=2\sqrt{5}
\end{align*}
2直線の交点の軌跡【富山大】
2015年 富山大$m$ を実数とする。方程式
(1) $xy$ 平面において,方程式(*)が表す図形は2直線であることを示せ。
(2) (1)で求めた2直線は $m$ の値にかかわらず,それぞれ定点を通る。これらの定点を求めよ。
(3) $m$ が $-1\leqq m\leqq3$ の範囲を動くとき,(1)で求めた2直線の交点の軌跡を図示せよ。
\begin{align*}
mx^2-my^2+(1-m^2)xy+5(1+m^2)y-25m=0~\cdots\cdots(*)
\end{align*}
を考える。このとき,次の問いに答えよ。mx^2-my^2+(1-m^2)xy+5(1+m^2)y-25m=0~\cdots\cdots(*)
\end{align*}
(1) $xy$ 平面において,方程式(*)が表す図形は2直線であることを示せ。
(2) (1)で求めた2直線は $m$ の値にかかわらず,それぞれ定点を通る。これらの定点を求めよ。
(3) $m$ が $-1\leqq m\leqq3$ の範囲を動くとき,(1)で求めた2直線の交点の軌跡を図示せよ。
【(1)の考え方と解答】
方程式(*)を因数分解しよう。(*)より
したがって,(*)は2直線①,②を表す。
方程式(*)を因数分解しよう。(*)より
\begin{align*}
&mx^2+(1-m^2)yx-\{my^2-5(1+m^2)y+25m\}=0 \\[4pt]
&mx^2+(1-m^2)yx-(my-5)(y-5m)=0 \\[4pt]
&(mx+y-5m)(x-my+5)=0 \\[4pt]
&mx+y-5m=0~\cdots\cdots① \\[4pt]
&または~~x-my+5~\cdots\cdots②
\end{align*}
ここで,①と②について&mx^2+(1-m^2)yx-\{my^2-5(1+m^2)y+25m\}=0 \\[4pt]
&mx^2+(1-m^2)yx-(my-5)(y-5m)=0 \\[4pt]
&(mx+y-5m)(x-my+5)=0 \\[4pt]
&mx+y-5m=0~\cdots\cdots① \\[4pt]
&または~~x-my+5~\cdots\cdots②
\end{align*}
\begin{align*}
m\Cdota1+1\Cdota(-m)=0
\end{align*}
が成り立つから,①と②は直交する2直線である。m\Cdota1+1\Cdota(-m)=0
\end{align*}
したがって,(*)は2直線①,②を表す。
(2) (1)で求めた2直線は $m$ の値にかかわらず,それぞれ定点を通る。これらの定点を求めよ。
【(2)の考え方と解答】
①を $m$ について整理すると
よって,直線①は $m$ の値にかかわらず定点 $(-5,~0)$ を通る。
②を $m$ について整理すると
よって,直線②は $m$ の値にかかわらず定点 $(5,~0)$ を通る。
①を $m$ について整理すると
\begin{align*}
m(x-5)+y=0
\end{align*}
となるから,$m$ の値にかかわらず①が成り立つのはm(x-5)+y=0
\end{align*}
\begin{align*}
x-5=0~かつ~~y=0
\end{align*}
となるとき,すなわち $x=5,~y=0$ となるときである。x-5=0~かつ~~y=0
\end{align*}
よって,直線①は $m$ の値にかかわらず定点 $(-5,~0)$ を通る。
②を $m$ について整理すると
\begin{align*}
(x+5)-my=0
\end{align*}
となるから,$m$ の値にかかわらず②が成り立つのは(x+5)-my=0
\end{align*}
\begin{align*}
x+5=0~かつ~~y=0
\end{align*}
となるとき,すなわち $x=-5,~y=0$ となるときである。x+5=0~かつ~~y=0
\end{align*}
よって,直線②は $m$ の値にかかわらず定点 $(5,~0)$ を通る。
(3) $m$ が $-1\leqq m\leqq3$ の範囲を動くとき,(1)で求めた2直線の交点の軌跡を図示せよ。
【(3)の考え方と解答】
2直線①,②が直交することと,①が定点A$(-5,~0)$ を通り,②が定点B$(5,~0)$ を通ることを考えると,2直線の交点Pは線分ABを直径とする円 $x^2+y^2=25$ 上を動くことが分かる。
ここで,2直線①,②が表せない直線に着目しよう。直線①は $y$ 軸と平行な直線と一致しないし,直線②は $x$ 軸と平行な直線と一致しない。それに加えて,$m$ の範囲が定められているため,2直線が動ける範囲はさらに制限される。
$m$ が $-1\leqq m\leqq3$ の範囲を動くとき,直線①の傾き $-m$ は $-3\leqq-m\leqq1$ の範囲を動く。$m=-1$ のとき,2直線①,②はそれぞれ
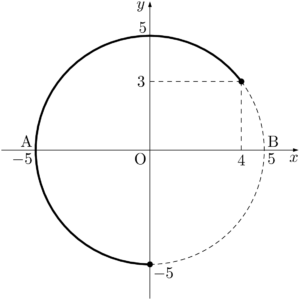
したがって,交点Pの軌跡は次の図のようになる。
2直線①,②が直交することと,①が定点A$(-5,~0)$ を通り,②が定点B$(5,~0)$ を通ることを考えると,2直線の交点Pは線分ABを直径とする円 $x^2+y^2=25$ 上を動くことが分かる。
ここで,2直線①,②が表せない直線に着目しよう。直線①は $y$ 軸と平行な直線と一致しないし,直線②は $x$ 軸と平行な直線と一致しない。それに加えて,$m$ の範囲が定められているため,2直線が動ける範囲はさらに制限される。
$m$ が $-1\leqq m\leqq3$ の範囲を動くとき,直線①の傾き $-m$ は $-3\leqq-m\leqq1$ の範囲を動く。$m=-1$ のとき,2直線①,②はそれぞれ
\begin{align*}
-x+y+5=0,~x+y+5=0
\end{align*}
となり,その交点は $(0,~-5)$ である。また,$m=3$ のとき,2直線①,②はそれぞれ-x+y+5=0,~x+y+5=0
\end{align*}
\begin{align*}
3x+y-15=0,~x-3y+5=0
\end{align*}
となり,その交点は $(4,~3)$ である。3x+y-15=0,~x-3y+5=0
\end{align*}
したがって,交点Pの軌跡は次の図のようになる。



















