根号を含む不等式といっても，外せる根号を含む不等式を扱います。
根号を外す際は絶対値記号を用いて表さないといけないため，根号を外した後は絶対値を含む不等式を解くことになります。
根号を外す問題と絶対値を含む不等式の融合問題とも言えます。
【数学Ⅰ】定期テストに出題される根号と絶対値に関する問題
「絶対値」という言葉を聞いたり「絶対値記号」を見た瞬間に「解けない問題だ」と思う人がいますが，かなり損をしています。 しっかり理解する気持ちがあれば，それほど難しいものではありません。 初めから理解する気もない状態で説明を聞いても，当然理解...
methodology.site
2020.03.05
【数学Ⅰ】定期テストに出題される絶対値を含む不等式
ここでは絶対値を含む不等式の解法について説明します。 「絶対値」を見るだけで拒絶反応をおこして問題を解こうとしないのは得策ではありません。 正しい考え方を知って，落ち着いて取り組むことで必ず解けるようになります。 それでは実際に定期テストで...
methodology.site
2020.03.10
テストで出題されても困らないように，しっかり対策しておきましょう。
Contents
定期テストに出題された問題
ヒロ
それでは次の問題を考えよう。
問題不等式 $\sqrt{x^2+4x+4}-2\sqrt{x^2-6x+9}\leqq3$ を解け。
ヒロ
まずは根号を外していこう。
【問題の考え方と解法】
与えられた不等式より
(i) $x<-2$ のとき
(ii) $-2\leqq x<3$ のとき
(iii) $3\leqq x$ のとき
(i)～(iii)より，$x\leqq\dfrac{7}{3},~5\leqq x$
与えられた不等式より
\begin{align*}
&\sqrt{(x+2)^2}-2\sqrt{(x-3)^2}\leqq3 \\[4pt]
&\abs{x+2}-2\abs{x-3}\leqq3
\end{align*}
&\sqrt{(x+2)^2}-2\sqrt{(x-3)^2}\leqq3 \\[4pt]
&\abs{x+2}-2\abs{x-3}\leqq3
\end{align*}
(i) $x<-2$ のとき
\begin{align*} &-(x+2)+2(x-3)\leqq3 \\[4pt] &x-8\leqq3 \\[4pt] &x\leqq11 \end{align*}
$x<-2$ との共通部分を考えて $x<-2$(ii) $-2\leqq x<3$ のとき
\begin{align*} &(x+2)+2(x-3)\leqq3 \\[4pt] &3x-4\leqq3 \\[4pt] &x\leqq\dfrac{7}{3} \end{align*}
$-2\leqq x<3$ との共通部分を考えて $-2\leqq x\leqq\dfrac{7}{3}$(iii) $3\leqq x$ のとき
\begin{align*} &(x+2)-2(x-3)\leqq3 \\[4pt] &-x+8\leqq3 \\[4pt] &x\geqq5 \end{align*}
$3\leqq x$ との共通部分を考えて $5\leqq x$(i)～(iii)より，$x\leqq\dfrac{7}{3},~5\leqq x$
グラフを利用した解法
ヒロ
次にグラフを利用して解こう。
ヒロ
と言っても，根号を外すまでは同じなので次の問題を考える。
$\abs{x+2}-2\abs{x-3}\leqq3$ を解け。
【グラフを利用した解答】
左辺を $f(x)$ として $y=f(x)$ のグラフを考える。
$f(x)$ の $x$ の係数は次のようになる。
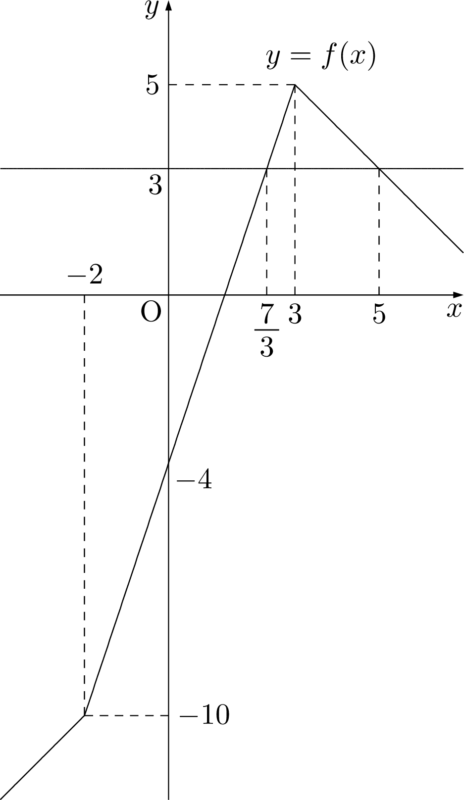
$y=f(x)$ のグラフが $y=3$ のグラフより下側にある範囲が求める解だから
左辺を $f(x)$ として $y=f(x)$ のグラフを考える。
$f(x)$ の $x$ の係数は次のようになる。
\begin{align*}
\begin{array}{c|c|c|c|c|c}
x & \cdots & -2 & \cdots & 3 & \cdots \\[4pt]\hline
x~の係数 & 1 & & 3 & & -1
\end{array}
\end{align*}
また，\begin{array}{c|c|c|c|c|c}
x & \cdots & -2 & \cdots & 3 & \cdots \\[4pt]\hline
x~の係数 & 1 & & 3 & & -1
\end{array}
\end{align*}
\begin{align*}
&f(-2)=-10 \\[4pt]&f(3)=5
\end{align*}
であるから $y=f(x)$ のグラフは次のようになる。&f(-2)=-10 \\[4pt]&f(3)=5
\end{align*}
$y=f(x)$ のグラフが $y=3$ のグラフより下側にある範囲が求める解だから
\begin{align*}
x\leqq\dfrac{7}{3},~5\leqq x
\end{align*}
x\leqq\dfrac{7}{3},~5\leqq x
\end{align*}