ここでは絶対値を含む不等式の解法について説明します。
「絶対値」を見るだけで拒絶反応をおこして問題を解こうとしないのは得策ではありません。
正しい考え方を知って,落ち着いて取り組むことで必ず解けるようになります。
それでは実際に定期テストで出題された問題を扱って説明していきます。
Contents
定期テストに出題された問題1

それでは次の問題を考えよう。
場合分けをする解法

この問題では絶対値の中身が $2x-3$ という文字で表された式のため,$x$ の値の範囲によって符号が変わるね。

ということは場合分けですね!

その方針で解いてみよう。
$2x-3\geqq0$ のときと $2x-3<0$ のときで場合分けしよう。
(i) $2x-3\geqq0$ すなわち $x\geqq\dfrac{3}{2}$ のとき $\abs{2x-3}=2x-3$ であるから
(ii) $2x-3<0$ すなわち $x<\dfrac{3}{2}$ のとき $\abs{2x-3}=-2x+3$ であるから
(i),(ii)より

いまは場合分けをしているため,「①または②」が求める解となることを理解しよう。
①が表す範囲は次のようになる。
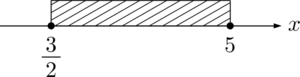
②が表す範囲は次のようになる。
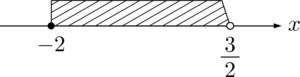
1つの数直線上に表すと次のようになる。


①と②が $x=\dfrac{3}{2}$ でつながっていることが分かるだろう。

いま考えているのは「①または②」だから,$-2\leqq x\leqq5$ になることが分かる。
絶対値の性質を考える解法
不等式 $\abs{2x-3}\leqq7$ を解け。

このタイプの不等式なら,場合分けをすることなく解くこともできる。

そのために,絶対値の性質の別の捉え方も知っておこう。

上の図は $a$ を正の数としたものであるが,$a$ が負の数でも,2点 $0,~a$ の距離を $\abs{a}$ と表すことは変わらない。
また,2点 $\mathrm{A}(a)$,$\mathrm{B}(b)$ の距離は $a$ と $b$ の大小関係にかかわらず $\abs{a-b}$ と表すことができる。


このことを考えて,問題1の不等式を解くと解答は2通り考えられ,次のようになる。
2点 $0$ と $2x-3$ の距離が7以下であるから
&-7\leqq2x-3\leqq7 \\[4pt]
&-4\leqq2x\leqq10 \\[4pt]
&-2\leqq x\leqq5
\end{align*}

もう1つの別解は次のようになる。
2点 $2x$ と $3$ の距離が7以下であるから
&-4\leqq2x\leqq10 \\[4pt]
&-2\leqq x\leqq5
\end{align*}

この解答は,中1で学習する正負の数を理解していれば簡単に理解できるはず。

くどいかもしれないが,もう一言付け加えておこう。

3より7小さい数は $-4$ で,3より7大きい数は10ということを考えて解いているだけだね。

この程度なら暗算で解を求めることができるようになるだろう。

そうなると,今まで絶対値で悩んでいたことがあほらしく感じるようになる。

実際そうなることを願う。
グラフを利用する解法
不等式 $\abs{2x-3}\leqq7$ を解け。

グラフを利用する解法を紹介しておこう。
$y=\abs{2x-3}$ のグラフと $y=7$ のグラフを描くと次のように
なる。交点の $x$ 座標については,
2x-3=7,~-2x+3=7
\end{align*}
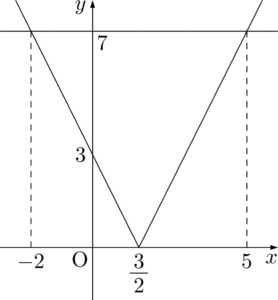
不等式の意味をグラフで捉えると,$\abs{2x-3}\leqq7$ は $y=\abs{2x-3}$ のグラフが $y=7$ のグラフより下側(等しくなる点を含む)にあるということである。
グラフを見て確認すると,$-2\leqq x\leqq5$ であることが分かる。
定期テストに出題された問題2

場合分けをする方法とグラフを利用する方法の2通りで解いておこう。
場合分けをする解法

絶対値の中身が $x-3$ だから,$x\geqq3$ と $x<3$ の2通りに場合分けをして考えよう。
(i) $x<3$ のとき $\abs{x-3}=-x+3$ であるから
(ii) $x\geqq3$ のとき $\abs{x-3}=x-3$ であるから
よって,(i),(ii)より $x\leqq-3$

今回の問題では(ii)のときに「解なし」になるのが難しいと思う。

式だけで処理することが苦手な人はグラフを利用して解くと良いかもね。
グラフを利用する解法
不等式 $\abs{x-3}\leqq-2x$ を解け。

$y=(左辺)$,$y=(右辺)$ として,2つのグラフの上限関係から解を求めよう。
$y=\abs{x-3}$ と $y=-2x$ のグラフを描くと次のようになる。
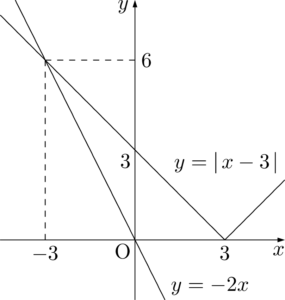
グラフにおいて,$y=\abs{x-3}$ のグラフが $y=-2x$ のグラフより下側にある範囲を考えると,求める解は $x\leqq-3$ となる。
定期テストに出題された問題3
場合分けをする解法

まずは場合分けをする解法で解こう。

場合分けをして解くたびに,場合分けの範囲との共通部分を考えるようにしよう。
グラフを利用する解法
不等式 $\abs{x}+\abs{x-2}<x+1$ を解け。
グラフを利用した解法でも解いておこう。
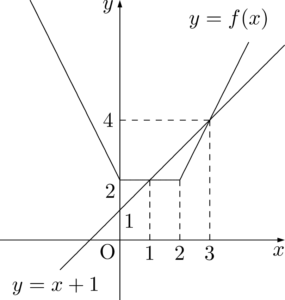
$y=f(x)$ のグラフが $y=x+1$ のグラフより下側にある範囲を考えると,求める解は


















