複数のアルファベットを使ってできる順列を辞書式に並べたときに関する問題の考え方を説明します。
具体的な問題としては,次のようなものがあります。
- 特定の文字列が何番目かを求める問題
- ○番目に現れる文字列を求める問題
そもそも「辞書式に並べる」とはどういう意味か分からない人はもちろん,意味は分かるけど苦手な人も,この記事を読むことで解けるようになるでしょう。
辞書式に並べるとは?

ヒロ
まず「辞書式配列」について理解しよう。
辞書式配列とは?
【辞書式配列】
今の時代,分からない単語があっても電子辞書などで調べる人が多いかもしれない。紙の辞書を実際に手に取って見たことがない人にとっては「辞書式」の意味が分からないのも当然とも言える。
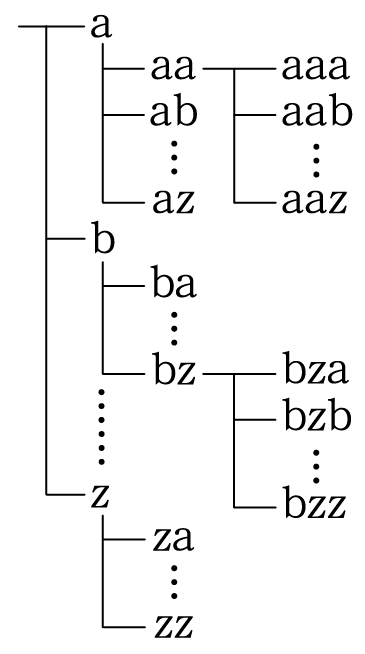
紙の英和辞典には,多くの単語が載っているが,最初は「a」から始まる単語が載っている。「a」から始まる単語が終われば,「b」から始まる単語が載っている。最後は「z」から始まる単語が載っている。つまり「辞書式に並べる」とは「アルファベット順に並べる」と読み取っても良い。「辞書式に並べる」の意味が分からない人が多数派になれば「アルファベット順に並べる」と表記が変わるかもしれない。
さて,「a」から始まる単語だけに着目した場合,その中でもアルファベット順に英単語が載っている。つまり「aa」から始まる単語から始まり,「az」から始まる単語で終わる。さらに「aa」から始まる単語の中は「aaa」から始まる単語から始まり,「aaz」から始まる単語で終わる。
1文字目を「a」で固定した場合,2文字目以降をアルファベット順にしていくことになる。また,2文字目を固定した場合は3文字目をアルファベット順に変えていくことになる。
今の時代,分からない単語があっても電子辞書などで調べる人が多いかもしれない。紙の辞書を実際に手に取って見たことがない人にとっては「辞書式」の意味が分からないのも当然とも言える。
紙の英和辞典には,多くの単語が載っているが,最初は「a」から始まる単語が載っている。「a」から始まる単語が終われば,「b」から始まる単語が載っている。最後は「z」から始まる単語が載っている。つまり「辞書式に並べる」とは「アルファベット順に並べる」と読み取っても良い。「辞書式に並べる」の意味が分からない人が多数派になれば「アルファベット順に並べる」と表記が変わるかもしれない。
さて,「a」から始まる単語だけに着目した場合,その中でもアルファベット順に英単語が載っている。つまり「aa」から始まる単語から始まり,「az」から始まる単語で終わる。さらに「aa」から始まる単語の中は「aaa」から始まる単語から始まり,「aaz」から始まる単語で終わる。
1文字目を「a」で固定した場合,2文字目以降をアルファベット順にしていくことになる。また,2文字目を固定した場合は3文字目をアルファベット順に変えていくことになる。


ヒロ
辞書式配列について理解できなかった場合は,実際の英和辞典を手に取って単語がどのような順番で載っているか確認して欲しい。

ヒロ
「百聞は一見にしかず」だ。

ヒロ
辞書式配列について理解できたとして話を進める。

ヒロ
「辞書式に並べる」の意味を理解しよう。
【辞書式に並べる例】
例えばtwiceという単語はt, w, i, c, eの5つのアルファベットをすべて使ってできる文字列の1つである。この5つのアルファベットを使ってできる文字列を辞書式に並べる,つまりアルファベット順に並べると,最初の文字列は「ceitw」となる。2番目の文字列は最初の3文字ceiは変えないで,最後の2文字tとwの順番を変えて「ceiwt」となる。3番目の文字列は最初の2文字ceを変えず,3文字目のiをtに変えて,4文字目以降は残っているiとwをアルファベット順に並べて「cetiw」となる。
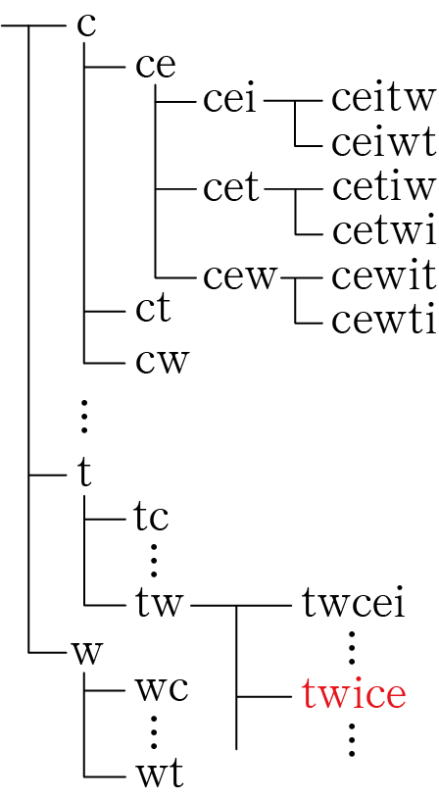
例えばtwiceという単語はt, w, i, c, eの5つのアルファベットをすべて使ってできる文字列の1つである。この5つのアルファベットを使ってできる文字列を辞書式に並べる,つまりアルファベット順に並べると,最初の文字列は「ceitw」となる。2番目の文字列は最初の3文字ceiは変えないで,最後の2文字tとwの順番を変えて「ceiwt」となる。3番目の文字列は最初の2文字ceを変えず,3文字目のiをtに変えて,4文字目以降は残っているiとwをアルファベット順に並べて「cetiw」となる。


ヒロ
異なる5つのものを並べる方法は $5!=120$ 通りあるから,最後の「wtiec」は120番目である。
辞書式に並べる例題

ヒロ
次の問題を解いておこう。
問題5つのアルファベットc, e, i, t, wをすべて使ってできる文字列を辞書式に並べるとき,「twice」は何番目の文字列か。
【考え方と解答】
「twice」はtから始まる文字列であることに注意する。
cから始まる文字列の個数は,残りのe, i, t, wの4文字を並べる方法に等しいから,$4!=24$ 個ある。
同じようにeから始まる文字列とiから始まる文字列もそれぞれ24個ある。
次はtから始まる文字列を考えるが,twiceがtから始まる文字列であるから,tから始まる文字列24個の途中にあるはずである。
したがって,2文字目も考える必要がある。つまり,tcから始まる文字列の個数から調べる。
t, c以外のe, i, wの3文字を並べる方法が $3!=6$ 通りあるから,tcから始まる文字列は6個ある。
同じように,teから始まる文字列とtiから始まる文字列もそれぞれ6個ある。
次にtwから始まる文字列を細かく調べる。twcから始まる文字列は,twcei,twcieの2個ある。
同様に,tweから始まる文字列も2個ある。この後,twiceが現れる。
したがって,twiceは最初から数えると
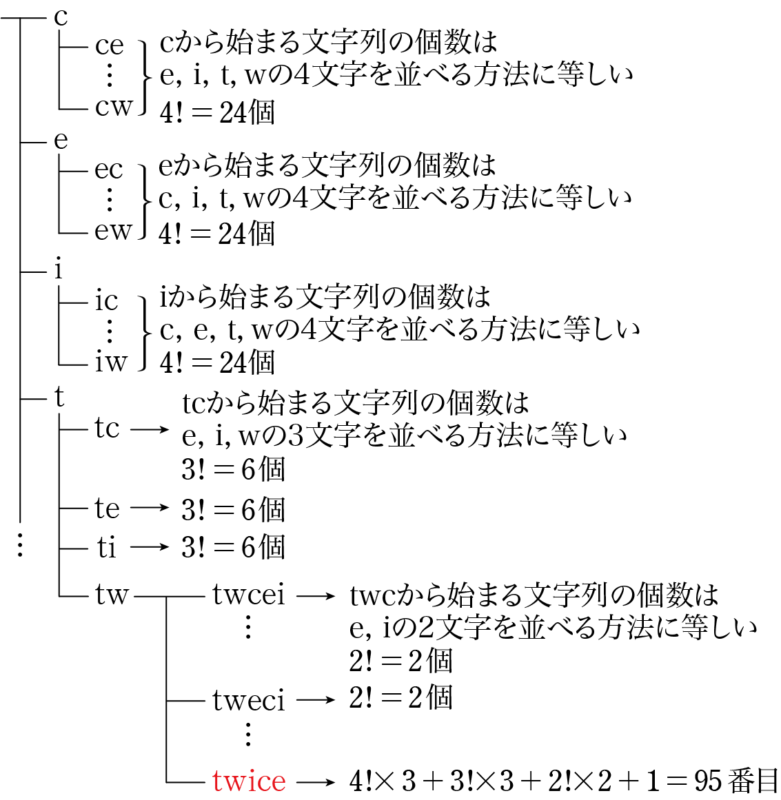
「twice」はtから始まる文字列であることに注意する。
cから始まる文字列の個数は,残りのe, i, t, wの4文字を並べる方法に等しいから,$4!=24$ 個ある。
同じようにeから始まる文字列とiから始まる文字列もそれぞれ24個ある。
次はtから始まる文字列を考えるが,twiceがtから始まる文字列であるから,tから始まる文字列24個の途中にあるはずである。
したがって,2文字目も考える必要がある。つまり,tcから始まる文字列の個数から調べる。
t, c以外のe, i, wの3文字を並べる方法が $3!=6$ 通りあるから,tcから始まる文字列は6個ある。
同じように,teから始まる文字列とtiから始まる文字列もそれぞれ6個ある。
次にtwから始まる文字列を細かく調べる。twcから始まる文字列は,twcei,twcieの2個ある。
同様に,tweから始まる文字列も2個ある。この後,twiceが現れる。
したがって,twiceは最初から数えると
\begin{align*}
&4!\times3+3!\times3+2\times2+1 \\[4pt]
&=24\times3+6\times3+4+1 \\[4pt]
&=72+18+5 \\[4pt]
&=95~番目
\end{align*}
&4!\times3+3!\times3+2\times2+1 \\[4pt]
&=24\times3+6\times3+4+1 \\[4pt]
&=72+18+5 \\[4pt]
&=95~番目
\end{align*}


ヒロ
○○番目の文字列を求める問題も解いておこう。
問題5つのアルファベットc, e, i, t, wをすべて使ってできる文字列を辞書式に並べるとき,30番目の文字列を求めよ。
【考え方と解答】
異なる5個のものを1列に並べる方法が $5!=120$ 通りあるから,最後の文字列ではないことが分かる。
cから始まる文字列の個数は,残り4文字の並べ方の総数に等しく,$4!=24$ 個ある。よって,30番目の文字列は,cから始まる文字列でないことが分かる。
eから始まる文字列も24個あることが分かる。$24+24=48>30$ となるから,30番目の文字列はeから始まることが分かる。
さらに詳しく調べる。
ecから始まる文字列の個数は,残り3文字の並べ方の総数に等しく,$3!=6$ 個ある。
$24+6=30$ となり,ちょうど30個になるから,求める30番目の文字列はecから始まる最後の文字列であることが分かる。
よって,求める文字列は,ecwtiである。
異なる5個のものを1列に並べる方法が $5!=120$ 通りあるから,最後の文字列ではないことが分かる。
cから始まる文字列の個数は,残り4文字の並べ方の総数に等しく,$4!=24$ 個ある。よって,30番目の文字列は,cから始まる文字列でないことが分かる。
eから始まる文字列も24個あることが分かる。$24+24=48>30$ となるから,30番目の文字列はeから始まることが分かる。
さらに詳しく調べる。
ecから始まる文字列の個数は,残り3文字の並べ方の総数に等しく,$3!=6$ 個ある。
$24+6=30$ となり,ちょうど30個になるから,求める30番目の文字列はecから始まる最後の文字列であることが分かる。
よって,求める文字列は,ecwtiである。
2020年 福島大

ヒロ
2020年の東京オリンピックは延期になったけど,福島大ではオリンピックに関連した問題が出題されている。
2020年 福島大(1) OLYMPICという単語の7文字のアルファベットすべてを使ってできる文字列の総数を求めなさい。
(2) (1)のすべての文字列を辞書式に並べたとき,OLYMPICは何番目になるか求めなさい。
(2) (1)のすべての文字列を辞書式に並べたとき,OLYMPICは何番目になるか求めなさい。

ヒロ
(1)は異なる7文字を並べるだけだから簡単だろう。
【(1)の解答】
異なる7文字を並べるから,求める文字列の総数は
異なる7文字を並べるから,求める文字列の総数は
\begin{align*}
7!=5040~個
\end{align*}
7!=5040~個
\end{align*}

ヒロ
(2)はアルファベット順に注意して丁寧に計算しよう。
【(2)の解答】
OLYMPICという単語の7文字のアルファベットを辞書式に並べたとき,最初の文字列はCILMOPYとなる。
C, I, L, Mから始まる文字列はそれぞれ $6!$ 個ある。
OC, OIから始まる文字列はそれぞれ $5!$ 個ある。
OLC, OLI, OLM, OLPから始まる文字列はそれぞれ $4!$ 個ある。
OLYC, OLYIから始まる文字列はそれぞれ $3!$ 個ある。
OLYMC, OLYMIから始まる文字列はそれぞれ $2!$ 個ある。
その後,OLYMPCI, OLYMPICと続く。
OLYMPICという単語の7文字のアルファベットを辞書式に並べたとき,最初の文字列はCILMOPYとなる。
C, I, L, Mから始まる文字列はそれぞれ $6!$ 個ある。
OC, OIから始まる文字列はそれぞれ $5!$ 個ある。
OLC, OLI, OLM, OLPから始まる文字列はそれぞれ $4!$ 個ある。
OLYC, OLYIから始まる文字列はそれぞれ $3!$ 個ある。
OLYMC, OLYMIから始まる文字列はそれぞれ $2!$ 個ある。
その後,OLYMPCI, OLYMPICと続く。
\begin{align*}
6!\times4+5!\times2+4!\times4+3!\times2+2!\times2+2=3234
\end{align*}
であるから,OLYMPICは3234番目である。6!\times4+5!\times2+4!\times4+3!\times2+2!\times2+2=3234
\end{align*}

ヒロ
アルファベット順に注意して,丁寧に計算することが重要である。


















