自然数の末尾に続く0の個数を求める方法を説明します。単純に方法だけを知るのではなく,
しっかりと理解することが重要です。
自然数の末尾に0が連続して並ぶ原理を理解することで,10進法で表された数だけでなく,
2進法で表された数に対しても,末尾に続く0の個数を求めることができるようになります。

ヒロ
まずは次の例題で末尾に0が並ぶことの意味を理解しよう。
例題$10\,!$を計算すると,末尾には0は連続して何個並ぶか。
Contents
末尾に並ぶ0の個数の求め方

ヒロ
$10\,!$ 程度なら簡単に計算できるようにしておこう。

ヒロ
そのためにも $7\,!=5040$ を覚えておくと良い。
【10!の末尾に並ぶ0の個数】
$7\,!=5040$ より
$7\,!=5040$ より
\begin{align*}
10\,!&=10\Cdota9\Cdota8\Cdota5040 \\[4pt]
&=3628800
\end{align*}
よって,$10\,!$ を計算すると末尾には0が2個並ぶ。10\,!&=10\Cdota9\Cdota8\Cdota5040 \\[4pt]
&=3628800
\end{align*}

ヒロ
ただ,この方法では,$2019\,!$ のような大きい数になると,末尾に並ぶ0の個数を求めることはできなくなる。

ヒロ
したがって,末尾に並ぶ0の意味を考えよう。
【素因数2と5の個数がポイント】
$10\,!$ を素因数分解すると,
\begin{align*}
10\,!&=10\Cdota9\Cdota8\Cdota7\Cdota6\Cdota5\Cdota4\Cdota3\Cdota2\Cdota1 \\[4pt]
&=2^8\Cdota3^4\Cdota5^2\Cdota7
\end{align*}
となる。$2\times5=10$ であるから,末尾の0に関わる数は2と5であり,できるだけ多く10を作ると10\,!&=10\Cdota9\Cdota8\Cdota7\Cdota6\Cdota5\Cdota4\Cdota3\Cdota2\Cdota1 \\[4pt]
&=2^8\Cdota3^4\Cdota5^2\Cdota7
\end{align*}
\begin{align*}
10\,!&=(2^6\Cdota3^4\Cdota7)\times10^2
\end{align*}
$2^6\Cdota3^4\Cdota7$ の部分からは10を作ることができないため,$10\,!$ の末尾には0が2個並ぶことになる。ここで,10がかけられている個数は,$10\,!$ を素因数分解したときに現れる素因数5の個数と一致することが分かる。10\,!&=(2^6\Cdota3^4\Cdota7)\times10^2
\end{align*}
これは素因数5が素因数2より少ないためである。
つまり,$10\,!$ に含まれる素因数5の個数を効率よく数えることができれば解決するということ。
10!に含まれる素因数2の個数の数え方

ヒロ
$10\,!$ を素因数分解したときの素因数5の個数は簡単に数えられるので,素因数2の個数を数えてみよう。
【それぞれの数に着目して素因数2の個数を数える】
10以下の自然数を1から1つずつ見て,2で1回割ることができれば黒丸を1つ書くことにすると,次のようになる。
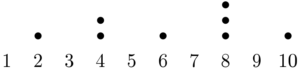
$2,~6,~10$ はそれぞれ2で1回しか割れないから黒丸が1つある。4は2で2回割ることができるから黒丸が2個ある。同様に8は2で3回割ることができるから黒丸が3個ある。この黒丸の総数が素因数2の個数である。左から右へ黒丸の個数を順に加えると,
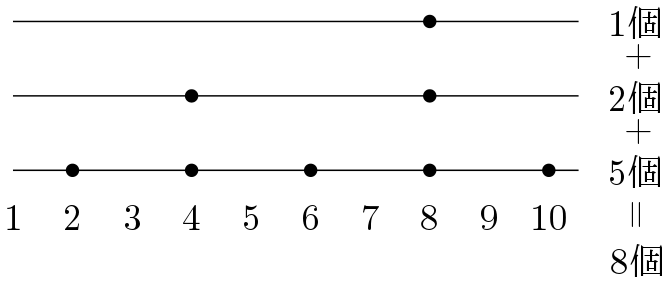
ただ,この方法では,大きい数になると数えられなくなる。したがって,縦に団子を作るのではなく,横に団子を作って数えてみよう。次のように,
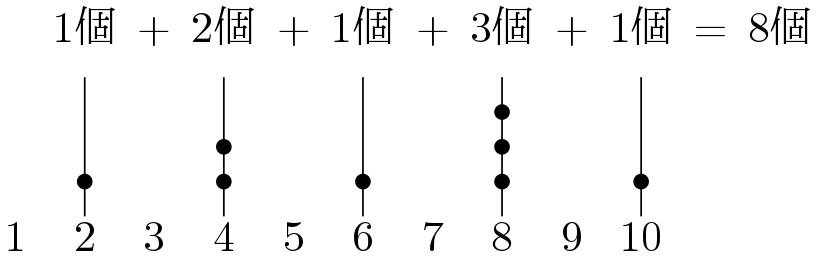
一番下の段は10以下の自然数のうち,2の倍数の個数を表している。また,二段目は4の倍数の個数,三段目は8の倍数の個数を表している。つまり,ガウス記号を用いると
10以下の自然数を1から1つずつ見て,2で1回割ることができれば黒丸を1つ書くことにすると,次のようになる。
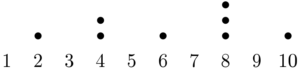
$2,~6,~10$ はそれぞれ2で1回しか割れないから黒丸が1つある。4は2で2回割ることができるから黒丸が2個ある。同様に8は2で3回割ることができるから黒丸が3個ある。この黒丸の総数が素因数2の個数である。左から右へ黒丸の個数を順に加えると,
\begin{align*}
1+2+1+3+1=8
\end{align*}
となる。1+2+1+3+1=8
\end{align*}

ただ,この方法では,大きい数になると数えられなくなる。したがって,縦に団子を作るのではなく,横に団子を作って数えてみよう。次のように,
\begin{align*}
5+2+1=8
\end{align*}
と黒丸の個数を数えることができる。5+2+1=8
\end{align*}

一番下の段は10以下の自然数のうち,2の倍数の個数を表している。また,二段目は4の倍数の個数,三段目は8の倍数の個数を表している。つまり,ガウス記号を用いると
\begin{align*}
&\left[\dfrac{10}{2}\right]+\left[\dfrac{10}{2^2}\right]+\left[\dfrac{10}{2^3}\right] \\[4pt]
&=5+2+1 \\[4pt]
&=8
\end{align*}
と計算することができる。また,この方法だと横方向は一気に計算できるため,大きい数になっても計算量はそこまで増えない利点がある。&\left[\dfrac{10}{2}\right]+\left[\dfrac{10}{2^2}\right]+\left[\dfrac{10}{2^3}\right] \\[4pt]
&=5+2+1 \\[4pt]
&=8
\end{align*}
2019!の末尾に並ぶ0の個数【2019年 藤田医科大】

ヒロ
2019年の藤田医科大の問題を解いてみよう。
2019年 藤田医科大$2019\,!$ の末尾には $\myhako{}$ 個の0が続いて並ぶ。

ヒロ
素因数5の個数を数えよう。
【解答】
$2019\,!$ に含まれる素因数5の個数は
$2019\,!$ に含まれる素因数5の個数は
\begin{align*}
&\left[\dfrac{2019}{5}\right]+\left[\dfrac{2019}{5^2}\right]
+\left[\dfrac{2019}{5^3}\right]+\left[\dfrac{2019}{5^4}\right] \\[4pt]
&=403+80+16+3 \\[4pt]
&=502
\end{align*}
よって,$2019\,!$ の末尾には502個の0が続いて並ぶ。&\left[\dfrac{2019}{5}\right]+\left[\dfrac{2019}{5^2}\right]
+\left[\dfrac{2019}{5^3}\right]+\left[\dfrac{2019}{5^4}\right] \\[4pt]
&=403+80+16+3 \\[4pt]
&=502
\end{align*}

ヒロ
これを計算するとき,それぞれの割り算をしなくても良い。

ヒロ
最初の $2019\div5$ を計算して商を求めたあとは,商を次々と5で割っていこう。
【商を次々と割っていけば良い】
\begin{align*}
&\left[\dfrac{2019}{5}\right]=403 \\[4pt]
&\left[\dfrac{403}{5}\right]=80 \\[4pt]
&\left[\dfrac{80}{5}\right]=16 \\[4pt]
&\left[\dfrac{16}{5}\right]=3
\end{align*}
&\left[\dfrac{2019}{5}\right]=403 \\[4pt]
&\left[\dfrac{403}{5}\right]=80 \\[4pt]
&\left[\dfrac{80}{5}\right]=16 \\[4pt]
&\left[\dfrac{16}{5}\right]=3
\end{align*}

ヒロ
この計算方法なら,素早く素因数5の個数を数えられるだろう。
2進法で表したときの末尾に並ぶ0の個数の求め方

ヒロ
次に2進法で表したときに,末尾に並ぶ0の個数を考えよう。
【2進法で表したときの末尾に並ぶ0】
2進法で表された自然数の末尾に続く0の個数が2だと言われた場合,$100_{(2)}$ や $1100_{(2)}$ などがある。 これらを10進法で表したとき,
一般化すると,2進法で表された自然数の末尾に続く0の個数が $m$ のとき, その自然数を10進法で表した数を $n$ とすると
2進法で表された自然数の末尾に続く0の個数が2だと言われた場合,$100_{(2)}$ や $1100_{(2)}$ などがある。 これらを10進法で表したとき,
\begin{align*}
100_{(2)}&=1\times2^2 \\[4pt]
1100_{(2)}&=2^3+2^2 \\[4pt]
&=3\times2^2
\end{align*}
となり,$2^2\times(奇数)$ と表せる。また,$1011000_{(2)}$ を10進法で表すと100_{(2)}&=1\times2^2 \\[4pt]
1100_{(2)}&=2^3+2^2 \\[4pt]
&=3\times2^2
\end{align*}
\begin{align*}
1011000_{(2)}&=2^6+2^4+2^3 \\[4pt]
&=(2^3+2+1)\times2^3 \\[4pt]
&=11\times2^3
\end{align*}
となる。2進法で表された自然数の末尾に続く0の個数が3のとき, その数を10進法で表すと,$2^3\times(奇数)$ と表せる。1011000_{(2)}&=2^6+2^4+2^3 \\[4pt]
&=(2^3+2+1)\times2^3 \\[4pt]
&=11\times2^3
\end{align*}
一般化すると,2進法で表された自然数の末尾に続く0の個数が $m$ のとき, その自然数を10進法で表した数を $n$ とすると
\begin{align*}
n=N\times2^m
\end{align*}
と表せる。ただし,$N$ を素因数分解したとき,2が現れることはない。 つまり,$N$ は奇数の素数の積である。n=N\times2^m
\end{align*}
20!を2進法で表したときの末尾に並ぶ0の個数

ヒロ
次の問題を解いてみよう。
練習問題$20\,!$ を2進法で表したとき,末尾に並ぶ0の個数を求めよ。

ヒロ
素因数2の個数に着目しよう。
【解答】
$20\,!$ に含まれる素因数2の個数は
$20\,!$ に含まれる素因数2の個数は
\begin{align*}
&\left[\dfrac{20}{2}\right]+\left[\dfrac{20}{2^2}\right]+\left[\dfrac{20}{2^3}\right]+\left[\dfrac{20}{2^4}\right] \\[4pt]
&=10+5+2+1 \\[4pt]
&=18
\end{align*}
となるから,$20\,!$ を2進法で表したとき,末尾には0が18個並ぶ。&\left[\dfrac{20}{2}\right]+\left[\dfrac{20}{2^2}\right]+\left[\dfrac{20}{2^3}\right]+\left[\dfrac{20}{2^4}\right] \\[4pt]
&=10+5+2+1 \\[4pt]
&=18
\end{align*}
2020!を2進法で表したときの末尾に並ぶ0の個数

ヒロ
もう1問解いておこう。
練習問題$2020\,!$ を2進法で表したとき,末尾に並ぶ0の個数を求めよ。

ヒロ
素因数2の個数に着目しよう。
【解答】
$2020\,!$ に含まれる素因数2の個数は
$2020\,!$ に含まれる素因数2の個数は
\begin{align*}
&\left[\dfrac{2020}{2}\right]+\left[\dfrac{2020}{2^2}\right]+\left[\dfrac{2020}{2^3}\right]+\left[\dfrac{2020}{2^4}\right] \\[4pt]
&\quad+\left[\dfrac{2020}{2^5}\right]+\left[\dfrac{2020}{2^6}\right]+\left[\dfrac{2020}{2^7}\right] \\[4pt]
&\quad+\left[\dfrac{2020}{2^8}\right]+\left[\dfrac{2020}{2^9}\right]+\left[\dfrac{2020}{2^{10}}\right] \\[4pt]
&=1010+505+252+126+63+31+15+7+3+1 \\[4pt]
&=2013
\end{align*}
となるから,$2020\,!$ を2進法で表したとき,末尾には0が2013個並ぶ。&\left[\dfrac{2020}{2}\right]+\left[\dfrac{2020}{2^2}\right]+\left[\dfrac{2020}{2^3}\right]+\left[\dfrac{2020}{2^4}\right] \\[4pt]
&\quad+\left[\dfrac{2020}{2^5}\right]+\left[\dfrac{2020}{2^6}\right]+\left[\dfrac{2020}{2^7}\right] \\[4pt]
&\quad+\left[\dfrac{2020}{2^8}\right]+\left[\dfrac{2020}{2^9}\right]+\left[\dfrac{2020}{2^{10}}\right] \\[4pt]
&=1010+505+252+126+63+31+15+7+3+1 \\[4pt]
&=2013
\end{align*}

ヒロ
ここまで理解していれば,2017年のセンターⅠA 整数の問題も大丈夫。



















