Contents
- ページ1
- ページ2
- 1 2019年 長崎大
- ページ3
- 1 2019年 大阪大
2019年 大阪大
2019年 大阪大実数 $s,~t$ が $s^2+t^2\leqq6$ を満たしながら変わるとき,$xy$ 平面上で点 $(s+t,~st)$ が動く領域を $A$ とする。このとき以下の問いに答えよ。
(1) $(2,~\sqrt{2})$ が領域 $A$ の点かどうか判定せよ。
(2) $A$ を図示せよ。
(1) $(2,~\sqrt{2})$ が領域 $A$ の点かどうか判定せよ。
(2) $A$ を図示せよ。
プリントを次のリンクからダウンロードできます。
【(1)の考え方と解答】
$(2,~\sqrt{2})$ が領域 $A$ の点であるとすると
したがって,$(2,~\sqrt{2})$ は領域 $A$ の点ではない。
$(2,~\sqrt{2})$ が領域 $A$ の点であるとすると
\begin{align*}
s+t=2,~st=\sqrt{2}
\end{align*}
をみたす実数 $s,~t$ が存在する。$s,~t$ を2解とする $X$ の2次方程式の1つはs+t=2,~st=\sqrt{2}
\end{align*}
\begin{align*}
&X^2-(s+t)X+st=0 \\[4pt]
&X^2-2X+\sqrt{2}=0~\cdots\cdots(*)
\end{align*}
である。判別式を $D$ とすると&X^2-(s+t)X+st=0 \\[4pt]
&X^2-2X+\sqrt{2}=0~\cdots\cdots(*)
\end{align*}
\begin{align*}
\dfrac{D}{4}=1-\sqrt{2}<0 \end{align*}
となるから(*)は実数解をもたない。つまり,条件をみたす実数 $s,~t$ は存在しない。\dfrac{D}{4}=1-\sqrt{2}<0 \end{align*}
したがって,$(2,~\sqrt{2})$ は領域 $A$ の点ではない。

ヒロ
(1)では,次のことが重要である。
$s+t$ と $st$ の値が与えられたときに,実際にそうなる実数 $s,~t$ の値が存在するかどうかを確認することが重要である。$s,~t$ が存在した場合に,さらに $s^2+t^2\leqq6$ を満たすかどうかを確認すればよい。
実数 $s,~t$ の存在を確認することなく,$s^2+t^2\leqq6$ を満たすかどうかを確認すると間違った結果が得られるだろう。
【間違った結果】
$s+t=2,~st=\sqrt{2}$ のとき
よって,$(2,~\sqrt{2})$ は領域 $A$ の点である。
$s+t=2,~st=\sqrt{2}$ のとき
\begin{align*} 6-(s^2+t^2)&=6-(s+t)^2+2st \\[4pt] &=6-2^2+2\sqrt{2} \\[4pt] &=2+2\sqrt{2}>0
\end{align*}
となるから,$s^2+t^2\leqq6$ が成り立つ。\end{align*}
よって,$(2,~\sqrt{2})$ は領域 $A$ の点である。
(2) $A$ を図示せよ。
【(2)の考え方と解答】
(1)があるおかげで,かなり解きやすくなっているだろう。点 $(s+t,~st)$ の軌跡を求めるために,$x=s+t$,$y=st$ とおくと,$s,~t$ を2解とする $X$ の2次方程式の1つは
したがって,求める領域 $A$ は下図の斜線部分(境界を含む)である。
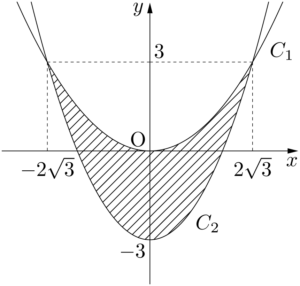
(1)があるおかげで,かなり解きやすくなっているだろう。点 $(s+t,~st)$ の軌跡を求めるために,$x=s+t$,$y=st$ とおくと,$s,~t$ を2解とする $X$ の2次方程式の1つは
\begin{align*}
X^2-xX+y=0
\end{align*}
であり,判別式を $D_2$ とするとX^2-xX+y=0
\end{align*}
\begin{align*}
&D_2=x^2-4y\geqq0 \\[4pt]
&y\leqq\dfrac{1}{4}x^2~\cdots\cdots①
\end{align*}
また,$s^2+t^2\leqq6$ より&D_2=x^2-4y\geqq0 \\[4pt]
&y\leqq\dfrac{1}{4}x^2~\cdots\cdots①
\end{align*}
\begin{align*}
&(s+t)^2-2st\leqq6 \\[4pt]
&x^2-2y\leqq6 \\[4pt]
&y\geqq\dfrac{1}{2}x^2-3~\cdots\cdots②
\end{align*}
①,②で表される領域が求める領域 $A$ である。$A$ の境界は2つの放物線&(s+t)^2-2st\leqq6 \\[4pt]
&x^2-2y\leqq6 \\[4pt]
&y\geqq\dfrac{1}{2}x^2-3~\cdots\cdots②
\end{align*}
\begin{align*}
C_1:y=\dfrac{1}{4}x^2,~C_2:y=\dfrac{1}{2}x^2-3
\end{align*}
である。交点を求める。二式から $y$ を消去するとC_1:y=\dfrac{1}{4}x^2,~C_2:y=\dfrac{1}{2}x^2-3
\end{align*}
\begin{align*}
&\dfrac{1}{2}x^2-3=\dfrac{1}{4}x^2 \\[4pt]
&x^2=12 \\[4pt]
&x=\pm2\sqrt{3}
\end{align*}
よって,2点 $(\pm2\sqrt{3},~3)$ で交わる。&\dfrac{1}{2}x^2-3=\dfrac{1}{4}x^2 \\[4pt]
&x^2=12 \\[4pt]
&x=\pm2\sqrt{3}
\end{align*}
したがって,求める領域 $A$ は下図の斜線部分(境界を含む)である。



















