Contents
- ページ1
- ページ2
- 1 2019年 長崎大
- ページ3
- 1 2019年 大阪大
2019年 長崎大
2019年 長崎大実数 $\alpha,~\beta~(\alpha\leqq\beta)$ に対し,$p,~q$ を $p=\alpha+\beta$,$q=\alpha\beta$ とする。以下の問いに答えよ。
(1) $p=3,~q=-1$ のとき,$\alpha$ と $\beta$ の値を求めよ。
(2) 実数 $\alpha,~\beta$ を解とする $x$ の2次方程式を $p,~q$ を用いて表せ。また,このときの $p,~q$ が満たす不等式を求めよ。
(3) (2)の実数 $\alpha,~\beta$ が,さらに不等式 $\alpha^2+\alpha\beta+\beta^2-3\leqq0$ を満たすとき,点P$(p,~q)$ が存在する領域 $E$ を $pq$ 平面に図示せよ。
(4) (3)のとき,$\alpha\beta+\alpha+\beta$ の最大値および最小値を求めよ。また,そのときの実数 $\alpha$ と $\beta$ の値を求めよ。
(1) $p=3,~q=-1$ のとき,$\alpha$ と $\beta$ の値を求めよ。
(2) 実数 $\alpha,~\beta$ を解とする $x$ の2次方程式を $p,~q$ を用いて表せ。また,このときの $p,~q$ が満たす不等式を求めよ。
(3) (2)の実数 $\alpha,~\beta$ が,さらに不等式 $\alpha^2+\alpha\beta+\beta^2-3\leqq0$ を満たすとき,点P$(p,~q)$ が存在する領域 $E$ を $pq$ 平面に図示せよ。
(4) (3)のとき,$\alpha\beta+\alpha+\beta$ の最大値および最小値を求めよ。また,そのときの実数 $\alpha$ と $\beta$ の値を求めよ。
【(1)の考え方と解答】
$p=3,~q=-1$ のとき,
$\alpha\leqq\beta$ より
$p=3,~q=-1$ のとき,
\begin{align*}
\alpha+\beta=3,~\alpha\beta=-1
\end{align*}
$\alpha,~\beta$ を2解とする $x$ の2次方程式の1つは\alpha+\beta=3,~\alpha\beta=-1
\end{align*}
\begin{align*}
x^2-3x-1=0
\end{align*}
であり,これを解くと,$x=\dfrac{3\pm\sqrt{13}}{2}$x^2-3x-1=0
\end{align*}
$\alpha\leqq\beta$ より
\begin{align*}
\alpha=\dfrac{3-\sqrt{13}}{2},~\beta=\dfrac{3+\sqrt{13}}{2}
\end{align*}
\alpha=\dfrac{3-\sqrt{13}}{2},~\beta=\dfrac{3+\sqrt{13}}{2}
\end{align*}
(2) 実数 $\alpha,~\beta$ を解とする $x$ の2次方程式を $p,~q$ を用いて表せ。また,このときの $p,~q$ が満たす不等式を求めよ。
【(2)の考え方と解答】
$p=\alpha+\beta$,$q=\alpha\beta$ より,$\alpha,~\beta$ を解とする $x$ の2次方程式の1つは
$p=\alpha+\beta$,$q=\alpha\beta$ より,$\alpha,~\beta$ を解とする $x$ の2次方程式の1つは
\begin{align*}
x^2-px+q=0~\cdots\cdots①
\end{align*}
である。$\alpha,~\beta$ は実数であるから,①は実数解をもつ。よって,判別式を $D$ とすると $D\geqq0$ が成り立つからx^2-px+q=0~\cdots\cdots①
\end{align*}
\begin{align*}
D=p^2-4q\geqq0~\cdots\cdots②
\end{align*}
D=p^2-4q\geqq0~\cdots\cdots②
\end{align*}
(3) (2)の実数 $\alpha,~\beta$ が,さらに不等式 $\alpha^2+\alpha\beta+\beta^2-3\leqq0$ を満たすとき,点P$(p,~q)$ が存在する領域 $E$ を $pq$ 平面に図示せよ。
【(3)の考え方と解答】
$\alpha^2+\alpha\beta+\beta^2-3\leqq0$ より
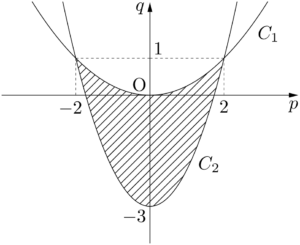
したがって,求める点Pが存在する領域 $E$ は下図の斜線部分(境界を含む)である。
$\alpha^2+\alpha\beta+\beta^2-3\leqq0$ より
\begin{align*}
&(\alpha+\beta)^2-\alpha\beta-3\leqq0 \\[4pt]
&p^2-q-3\leqq0 \\[4pt]
&q\geqq p^2-3~\cdots\cdots③
\end{align*}
②,③が表す領域の境界は2つの放物線&(\alpha+\beta)^2-\alpha\beta-3\leqq0 \\[4pt]
&p^2-q-3\leqq0 \\[4pt]
&q\geqq p^2-3~\cdots\cdots③
\end{align*}
\begin{align*}
C_1:q=\dfrac{1}{4}p^2,~C_2:q=p^2-3
\end{align*}
である。交点を求めるために $q$ を消去するとC_1:q=\dfrac{1}{4}p^2,~C_2:q=p^2-3
\end{align*}
\begin{align*}
&\dfrac{1}{4}p^2=p^2-3 \\[4pt]
&3p^2-12=0 \\[4pt]
&p=\pm2
\end{align*}
よって,2つの放物線は2点 $(-2,~1),~(2,~1)$ で交わる。&\dfrac{1}{4}p^2=p^2-3 \\[4pt]
&3p^2-12=0 \\[4pt]
&p=\pm2
\end{align*}
したがって,求める点Pが存在する領域 $E$ は下図の斜線部分(境界を含む)である。

(4) (3)のとき,$\alpha\beta+\alpha+\beta$ の最大値および最小値を求めよ。また,そのときの実数 $\alpha$ と $\beta$ の値を求めよ。
【(4)の考え方と解答】
(3)までで,$\alpha,~\beta$ ではなく,$p,~q$ で考えてきたから,$p,~q$ で表して考えよう。
$p=\alpha+\beta$,$q=\alpha\beta$ より,
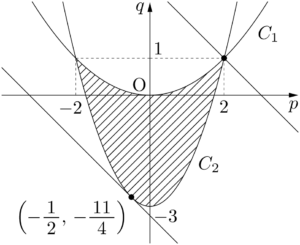
$p,~q$ は(3)の斜線部分にあるから,直線 $l:q=-p+k$ を斜線部分と共有点をもつように動かして,$k$ が最大になるときと最小になるときを求める。
$k$ が最大になるときは,直線 $l$ が点 $(2,~1)$ を通るときであるから,最大値は $2+1=3$ である。③より $\alpha,~\beta$ は
$k$ の最小値を求める。$k$ が最小になるときは,直線 $l$ が放物線 $C_2$ と接するときである。$l,~C_2$ の方程式から $q$ を消去すると
(3)までで,$\alpha,~\beta$ ではなく,$p,~q$ で考えてきたから,$p,~q$ で表して考えよう。
$p=\alpha+\beta$,$q=\alpha\beta$ より,
\begin{align*}
\alpha\beta+\alpha+\beta&=q+p
\end{align*}
$p+q=k$ とおくと,$q=-p+k$ となるから,これは $pq$ 平面では傾き $-1$,切片 $k$ の直線を表す。\alpha\beta+\alpha+\beta&=q+p
\end{align*}
$p,~q$ は(3)の斜線部分にあるから,直線 $l:q=-p+k$ を斜線部分と共有点をもつように動かして,$k$ が最大になるときと最小になるときを求める。
$k$ が最大になるときは,直線 $l$ が点 $(2,~1)$ を通るときであるから,最大値は $2+1=3$ である。③より $\alpha,~\beta$ は
\begin{align*}
x^2-2x+1=0
\end{align*}
の解である。これよりx^2-2x+1=0
\end{align*}
\begin{align*}
&(x-1)^2=0 \\[4pt]
&x=1
\end{align*}
よって,$\alpha=\beta=1$&(x-1)^2=0 \\[4pt]
&x=1
\end{align*}
$k$ の最小値を求める。$k$ が最小になるときは,直線 $l$ が放物線 $C_2$ と接するときである。$l,~C_2$ の方程式から $q$ を消去すると
\begin{align*}
&p^2-3=-p+k \\[4pt]
&p^2+p-k-3=0~\cdots\cdots④
\end{align*}
方程式④が重解をもつから,判別式を $D_2$ とすると&p^2-3=-p+k \\[4pt]
&p^2+p-k-3=0~\cdots\cdots④
\end{align*}
\begin{align*}
&D_2=1-4(-k-3)=0 \\[4pt]
&4k+13=0 \\[4pt]
&k=-\dfrac{13}{4}
\end{align*}
このとき④の重解は $p=-\dfrac{1}{2}$ であり,$q=-\dfrac{11}{4}$ となる。③より $\alpha,~\beta$ は&D_2=1-4(-k-3)=0 \\[4pt]
&4k+13=0 \\[4pt]
&k=-\dfrac{13}{4}
\end{align*}
\begin{align*}
x^2+\dfrac{1}{2}x-\dfrac{11}{4}=0
\end{align*}
の解である。これよりx^2+\dfrac{1}{2}x-\dfrac{11}{4}=0
\end{align*}
\begin{align*}
&4x^2+2x-11=0 \\[4pt]
&x=\dfrac{-1\pm3\sqrt{5}}{4}
\end{align*}
$\alpha\leqq\beta$ より,&4x^2+2x-11=0 \\[4pt]
&x=\dfrac{-1\pm3\sqrt{5}}{4}
\end{align*}
\begin{align*}
\alpha=\dfrac{-1-3\sqrt{5}}{4},~\beta=\dfrac{-1+3\sqrt{5}}{4}
\end{align*}
\alpha=\dfrac{-1-3\sqrt{5}}{4},~\beta=\dfrac{-1+3\sqrt{5}}{4}
\end{align*}




















