ここでは,ある領域内に動点があるとき,与えられた式の最大値や最小値を求める方法について説明します。
大学入試では,教科書には出てこないような式の最大値や最小値を求めさせる問題が出題されます。
「見たことがないから分からない」とならないように,「考え方」を身に付けましょう。
Contents
直線で囲まれる領域と分数式の最大・最小【学習院大】
2016年 学習院大連立不等式
\begin{align*}
2x-y-2\geqq0,~x\leqq\dfrac{5}{2},~y\geqq1
\end{align*}
の表す領域を $D$ とする。点P$(x,~y)$ が領域 $D$ を動くとき,$\dfrac{y}{x^2}$ の最大値と最小値を求めよ。また,それぞれの値を与える点Pの座標を求めよ。2x-y-2\geqq0,~x\leqq\dfrac{5}{2},~y\geqq1
\end{align*}
【考え方と解答】
分数式の最大値を求めるのかと驚く人もいるかもしれないが,$k$ とおいて調べよう。
$\dfrac{y}{x^2}=k$ とおくと,$y=kx^2$ と変形できるから,$k\neq0$ のとき,そのグラフは原点を頂点とする放物線となる。$\abs{k}$ が大きくなるほど放物線の開き具合が小さくなり,$\abs{k}$ が小さくなるほど放物線の開き具合が大きくなる。また,$k=0$ となるのは $y=0$ のときである。
領域 $D$ の境界線は3つの直線で,それらの方程式は次のようになる。
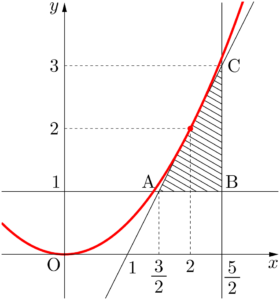
点 $(x,~y)$ は領域 $D$ 内を動くから,$\dfrac{y}{x^2}=k$ とおくと,$k>0$ となる。$y=kx^2$ と変形すると,グラフは原点を頂点とする下に凸の放物線であることが分かる。放物線 $y=kx^2$ が直線 $2x-y-2=0$ と接するときを考える。二式より $y$ を消去すると
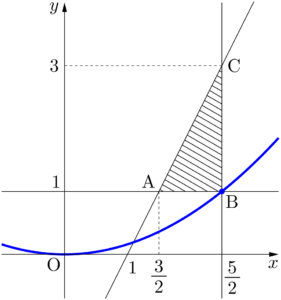
次に $k$ の最小値を求める。$k$ が最小になるのは,放物線 $y=kx^2$ が点Bを通るときであるから
したがって,$\dfrac{y}{x^2}$ は $(x,~y)=(2,~2)$ のとき,最大値 $\dfrac{1}{2}$ をとり,$(x,~y)=\left(\dfrac{5}{2},~1\right)$ のとき,最小値 $\dfrac{4}{25}$ をとる。
分数式の最大値を求めるのかと驚く人もいるかもしれないが,$k$ とおいて調べよう。
$\dfrac{y}{x^2}=k$ とおくと,$y=kx^2$ と変形できるから,$k\neq0$ のとき,そのグラフは原点を頂点とする放物線となる。$\abs{k}$ が大きくなるほど放物線の開き具合が小さくなり,$\abs{k}$ が小さくなるほど放物線の開き具合が大きくなる。また,$k=0$ となるのは $y=0$ のときである。
領域 $D$ の境界線は3つの直線で,それらの方程式は次のようになる。
\begin{align*}
2x-y-2=0,~x=\dfrac{5}{2},~y=1
\end{align*}
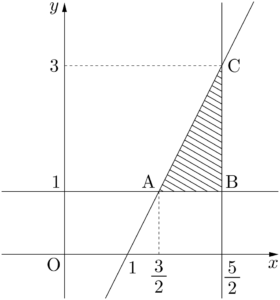
3直線の交点を求めると,A$\left(\dfrac{3}{2},~1\right)$,B$\left(\dfrac{5}{2},~1\right)$,C$\left(\dfrac{5}{2},~3\right)$ となり,領域 $D$ は下図の斜線部分(境界を含む)となる。2x-y-2=0,~x=\dfrac{5}{2},~y=1
\end{align*}

点 $(x,~y)$ は領域 $D$ 内を動くから,$\dfrac{y}{x^2}=k$ とおくと,$k>0$ となる。$y=kx^2$ と変形すると,グラフは原点を頂点とする下に凸の放物線であることが分かる。放物線 $y=kx^2$ が直線 $2x-y-2=0$ と接するときを考える。二式より $y$ を消去すると
\begin{align*}
kx^2-2x+2=0
\end{align*}
判別式を $D$ とすると $D=0$ よりkx^2-2x+2=0
\end{align*}
\begin{align*}
D/4=1-2k=0~~\therefore k=\dfrac{1}{2}
\end{align*}
このとき,接点の $x$ 座標はD/4=1-2k=0~~\therefore k=\dfrac{1}{2}
\end{align*}
\begin{align*}
x=\dfrac{1}{k}=2
\end{align*}
となるから,接点は線分AC上にある。したがって,$k$ の最大値は $\dfrac{1}{2}$ である。x=\dfrac{1}{k}=2
\end{align*}

次に $k$ の最小値を求める。$k$ が最小になるのは,放物線 $y=kx^2$ が点Bを通るときであるから
\begin{align*}
1=\left(\dfrac{5}{2}\right)^2k~~\therefore k=\dfrac{4}{25}
\end{align*}
1=\left(\dfrac{5}{2}\right)^2k~~\therefore k=\dfrac{4}{25}
\end{align*}

したがって,$\dfrac{y}{x^2}$ は $(x,~y)=(2,~2)$ のとき,最大値 $\dfrac{1}{2}$ をとり,$(x,~y)=\left(\dfrac{5}{2},~1\right)$ のとき,最小値 $\dfrac{4}{25}$ をとる。


















