ここでは図示された領域を不等式で表す方法について説明します。
大学入試では,与えられた不等式が表す領域を図示する問題が出題されることが多いのですが,図示された領域を不等式で表す問題が出題されることがあります。
境界線に着目して,図示された領域を表すような不等式を作ろう。
図示された領域を不等式で表す【獨協大】
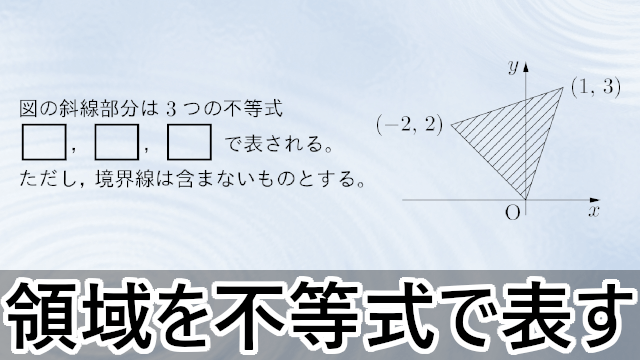
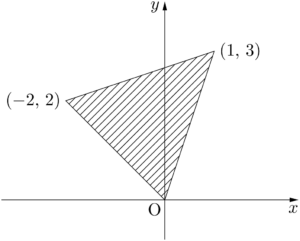
2011年 獨協大図の斜線部分は3つの不等式 $\myhako$,$\myhako$,$\myhako$ で表される。ただし,境界線は含まないものとする。

【考え方と解答】
まずは境界線となる3直線の方程式を求めよう。
2点 $(1,~3)$,$(-2,~2)$ をそれぞれA,Bとする。
直線OAは原点を通り,傾き3の直線であるから,その方程式は,$y=3x$
直線OBは原点を通り,傾き $-1$ の直線であるから,その方程式は,$y=-x$
直線ABは点Aを通り,傾き $\dfrac{3-2}{1-(-2)}=\dfrac{1}{3}$ の直線であるから,その方程式は
まずは境界線となる3直線の方程式を求めよう。
2点 $(1,~3)$,$(-2,~2)$ をそれぞれA,Bとする。
直線OAは原点を通り,傾き3の直線であるから,その方程式は,$y=3x$
直線OBは原点を通り,傾き $-1$ の直線であるから,その方程式は,$y=-x$
直線ABは点Aを通り,傾き $\dfrac{3-2}{1-(-2)}=\dfrac{1}{3}$ の直線であるから,その方程式は
\begin{align*}
&y=\dfrac{1}{3}(x-1)+3 \\[4pt]
&y=\dfrac{1}{3}x+\dfrac{8}{3}
\end{align*}
図で示された領域は,直線OAの上側かつ直線OBの上側かつ直線ABの下側であり,境界線を含まないから,3つの不等式&y=\dfrac{1}{3}(x-1)+3 \\[4pt]
&y=\dfrac{1}{3}x+\dfrac{8}{3}
\end{align*}
\begin{align*}
y>3x,~y>-x,~y<\dfrac{1}{3}x+\dfrac{8}{3} \end{align*}
で表される。y>3x,~y>-x,~y<\dfrac{1}{3}x+\dfrac{8}{3} \end{align*}