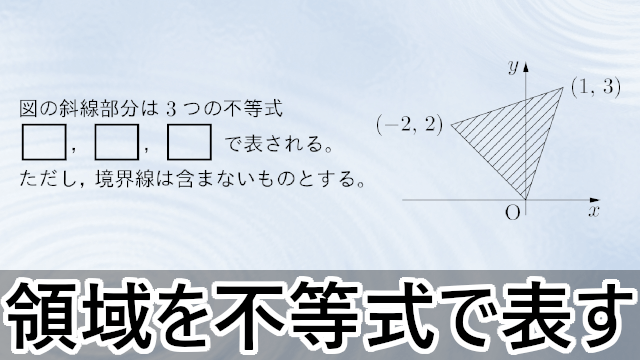
図示された領域を不等式で表す【広島国際学院大】
2012年 広島国際学院大図のように,円と2つの直線によって指定される領域がある。
(1) 斜線の領域を表す不等式を求めなさい。ただし,境界線を含むものとする。
(2) 斜線の領域の面積 $S$ を求めなさい。
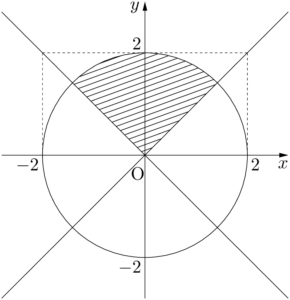
(1) 斜線の領域を表す不等式を求めなさい。ただし,境界線を含むものとする。
(2) 斜線の領域の面積 $S$ を求めなさい。

【(1)の考え方と解答】
境界線は円と2つの直線であり,それらの方程式を求める。
原点を中心とする半径2の円の方程式は $x^2+y^2=4$ である。
右上がりの直線は,原点を通り,傾きが1の直線であるから,その方程式は $y=x$ である。
右下がりの直線は,原点を通り,傾きが $-1$ の直線であるから,その方程式は $y=-x$ である。
図示された領域は,円の内部かつ2直線の上側であり,境界を含むから,求める不等式は次のようになる。
境界線は円と2つの直線であり,それらの方程式を求める。
原点を中心とする半径2の円の方程式は $x^2+y^2=4$ である。
右上がりの直線は,原点を通り,傾きが1の直線であるから,その方程式は $y=x$ である。
右下がりの直線は,原点を通り,傾きが $-1$ の直線であるから,その方程式は $y=-x$ である。
図示された領域は,円の内部かつ2直線の上側であり,境界を含むから,求める不等式は次のようになる。
\begin{align*}
x^2+y^2\leqq4~~かつ~~y\geqq x~~かつ~~y\geqq-x
\end{align*}
x^2+y^2\leqq4~~かつ~~y\geqq x~~かつ~~y\geqq-x
\end{align*}
(2) 斜線の領域の面積 $S$ を求めなさい。
【(2)の考え方と解答】
斜線部分は,半径2,中心角 $\dfrac{\pi}{2}$ の扇形であるから,求める面積 $S$ は
斜線部分は,半径2,中心角 $\dfrac{\pi}{2}$ の扇形であるから,求める面積 $S$ は
\begin{align*}
S=\dfrac{1}{2}\Cdota2^2\Cdota\dfrac{\pi}{2}=\pi
\end{align*}
S=\dfrac{1}{2}\Cdota2^2\Cdota\dfrac{\pi}{2}=\pi
\end{align*}
図示された領域を不等式で表す【大阪学院大】
2007年 大阪学院大次の図について,次の問いに答えなさい。
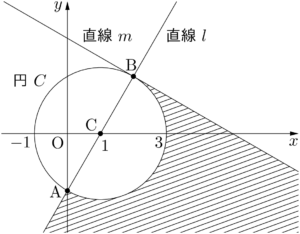
(1) 円 $C$ の中心は点C$(1,~0)$ である。この円の方程式を求めなさい。
(2) 点Aは円 $C$ と $y$ 軸の交点である。点Aの座標を求め,点Aと中心Cを通る直線 $l$ の方程式を求めなさい。
(3) 点Bは直線 $l$ と円 $C$ の交点である。点Bの座標を求め,点Bで円 $C$ と接する直線 $m$ の方程式を求めなさい。
(4) 斜線で示した領域(境界線は含まない)を連立不等式で表しなさい。

(1) 円 $C$ の中心は点C$(1,~0)$ である。この円の方程式を求めなさい。
(2) 点Aは円 $C$ と $y$ 軸の交点である。点Aの座標を求め,点Aと中心Cを通る直線 $l$ の方程式を求めなさい。
(3) 点Bは直線 $l$ と円 $C$ の交点である。点Bの座標を求め,点Bで円 $C$ と接する直線 $m$ の方程式を求めなさい。
(4) 斜線で示した領域(境界線は含まない)を連立不等式で表しなさい。
【(1)の考え方と解答】
円 $C$ は点C$(1,~0)$ を中心とする半径2の円であるから,その方程式は次のようになる。
円 $C$ は点C$(1,~0)$ を中心とする半径2の円であるから,その方程式は次のようになる。
\begin{align*}
(x-1)^2+y^2=4~\cdots\cdots①
\end{align*}
(x-1)^2+y^2=4~\cdots\cdots①
\end{align*}
(2) 点Aは円 $C$ と $y$ 軸の交点である。点Aの座標を求め,点Aと中心Cを通る直線 $l$ の方程式を求めなさい。
【(2)の考え方と解答】
点Aの座標を求める。①に $x=0$ を代入すると
よって,点Aの座標は $(0,~-\sqrt{3})$
直線 $l$ の傾きは $\sqrt{3}$ であるから,その方程式は,$y=\sqrt{3}x-\sqrt{3}$
点Aの座標を求める。①に $x=0$ を代入すると
\begin{align*}
&1+y^2=4 \\[4pt]
&y^2=3 \\[4pt]
&y=\pm\sqrt{3}
\end{align*}
$y<0$ より,$y=-\sqrt{3}$&1+y^2=4 \\[4pt]
&y^2=3 \\[4pt]
&y=\pm\sqrt{3}
\end{align*}
よって,点Aの座標は $(0,~-\sqrt{3})$
直線 $l$ の傾きは $\sqrt{3}$ であるから,その方程式は,$y=\sqrt{3}x-\sqrt{3}$
(3) 点Bは直線 $l$ と円 $C$ の交点である。点Bの座標を求め,点Bで円 $C$ と接する直線 $m$ の方程式を求めなさい。
【(3)の考え方と解答】
交点を求める問題だからといって,何も考えず連立方程式を解くのではなく,楽に解けるなら楽をしよう。
今回は,2点A,Bが直径の両端であり,一方が分かっていて,もう一方を求める問題である。また,直径の中点は円の中心で,この座標も分かっている。 B$(a,~b)$ とすると,ABの中点がC$(1,~0)$ であるから
交点を求める問題だからといって,何も考えず連立方程式を解くのではなく,楽に解けるなら楽をしよう。
今回は,2点A,Bが直径の両端であり,一方が分かっていて,もう一方を求める問題である。また,直径の中点は円の中心で,この座標も分かっている。 B$(a,~b)$ とすると,ABの中点がC$(1,~0)$ であるから
\begin{align*} &\dfrac{a+0}{2}=1,~\dfrac{b-\sqrt{3}}{2}=0 \\[4pt] &a=2,~b=\sqrt{3} \end{align*}
よって,点Bの座標は $(2,~\sqrt{3})$
ヒロ
堅苦しく書いたが,答えだけを求めるなら,一瞬で求めた人も多いかもしれない。
【対称性に着目する】
点Bから $x$ 軸に垂線BHを下ろして,$\sankaku{OAC}$ と $\sankaku{HBC}$ に着目する。
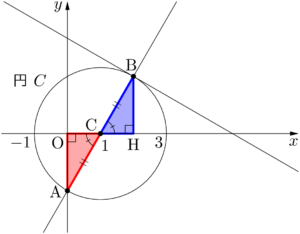
2つの三角形は直角三角形で,斜辺の長さと1つの鋭角の大きさが等しいから合同である。赤色で示した $\sankaku{OAC}$ を点Cのまわりに $180\Deg$ 回転させると青色で示した $\sankaku{HBC}$ に重なることを考えると,すぐに点Bの座標が $(2,~\sqrt{3})$ であると分かる。
(4) 斜線で示した領域(境界線は含まない)を連立不等式で表しなさい。
【(4)の考え方と解答】
直線 $m$ は直線 $l$ に垂直であるから,傾きは $-\dfrac{1}{\sqrt{3}}$ である。よって,直線 $m$ の方程式は
直線 $m$ は直線 $l$ に垂直であるから,傾きは $-\dfrac{1}{\sqrt{3}}$ である。よって,直線 $m$ の方程式は
\begin{align*} &y=-\dfrac{1}{\sqrt{3}}(x-2)+\sqrt{3} \\[4pt] &y=-\dfrac{1}{\sqrt{3}}x+\dfrac{5}{\sqrt{3}} \end{align*}
斜線で示された領域は円 $C$ の外部かつ2直線 $l,~m$ の下側(境界を含まない)であるから,求める連立不等式は次のようになる。 \begin{align*} \begin{cases} (x-1)^2+y^2>4 \\[4pt]
y<\sqrt{3}x-\sqrt{3} \\[4pt] y<-\dfrac{1}{\sqrt{3}}x+\dfrac{5}{\sqrt{3}} \end{cases} \end{align*}
y<\sqrt{3}x-\sqrt{3} \\[4pt] y<-\dfrac{1}{\sqrt{3}}x+\dfrac{5}{\sqrt{3}} \end{cases} \end{align*}