【数学ⅡB】3次関数の極値【東京電機大・大阪工業大・早稲田大】

【極値とならない例】
関数 $f(x)=x^3$ のグラフは次のようになっている。

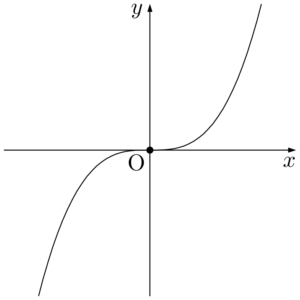
$f'(x)=3x^2$ であるから，$f'(0)=0$ となる。しかし，$x=0$ の前後で増減は変わらず，単調増加している。したがって，$f(x)$ は $x=0$ で極値をとるとはいえない。

【解答と考え方】
$f'(x)$ を求めるときに，積の微分法を用いても良いが，展開した方が楽だろう。$(x+2)(x-2)=x^2-4$ と簡単に展開できるから，各項に $x$ を掛けるだけ（次数を1上げるだけ）で展開できる。この計算は暗算でできるようになるだろう。
このとき
となるから $f'(x)=0$ を解くと，$x=\pm\dfrac{2}{\sqrt{3}}$
よって，$f(x)$ の増減は次のようになる。
よって，求める極大値は

【(1)の解答と考え方】
計算間違いをしないように微分しよう。
$f(x)=2ax^3-3(a+1)x^2+6x$ のとき

【(2)の解答と考え方】
まずは $f'(x)=0$ となる $x$ を求めて増減表を書こう。
$f'(x)$ の各項が6を因数にもつから，$f'(x)=0$ を解くときには，両辺を6で割ろう。
たすきがけで因数分解しても良いし，$a$ について整理して因数分解しても良い。$a$ について整理した場合は次のように $x-1$ でくくれることがすぐに分かる。

増減表を書くためには，1と $\dfrac{1}{a}$ の大小関係を考えなければならない。与えられている $a$ の条件を利用することを考えよう。
$0<a<1$ のとき，$a$ は正であるから，$\dfrac{1}{a}$ も正である。また，$a<1$ であるから，両辺を $a~(>0)$ で割ると，$1<\dfrac{1}{a}$ となる。まとめると，$\dfrac{1}{a}>1$ となるが，解答にはこんなに丁寧に書かずに，一気に，$\dfrac{1}{a}>1$ と書いてしまって良い。これで1と $\dfrac{1}{a}$ の大小関係が分かったから増減表を書くことができる。
$x=1$ のとき
$x=\dfrac{1}{a}$ のとき
極大値は $f(1)=-a+3$，極小値は $f\left(\dfrac{1}{a}\right)=\dfrac{3a-1}{a^2}$

【考え方】
　話をしやすいように，$x=\alpha,~\beta~(\alpha\neq\beta)$ でそれぞれ極大値，極小値をとるとする。関数 $f(x)$ が極大値および極小値をとるためには $f'(\alpha)=f'(\beta)=0$ が成り立つことが必要である。これは $f'(x)=0$ の2つの解が $x=\alpha,~\beta$ であると言い換えることができる。
　便宜上，$\alpha,~\beta$ と定めただけだから，$f'(x)=0$ が異なる2つの実数解をもつことが必要ということになる。あとは2つの解の前後で $f'(x)$ の符号が変化していれば，問題文で与えられた条件を満たすことになる。
　ここで，$f(x)$ は3次関数であるから，$f'(x)$ は2次関数となる。したがって，$f'(x)=0$ の実数解は放物線 $y=f'(x)$ と $x$ 軸との交点の $x$ 座標を表す。交点の前後で $f'(x)$ の符号は必ず変わるから，$f'(x)=0$ が異なる2つの実数解をもつことが，関数 $f(x)$ が極大値と極小値をとるための必要条件であり，十分条件であることが分かる。
　今回の問題のように，十分性を確認することが簡単であるときは，「問題文の条件を満たすのは○○のときである」とサクッと書いてしまえば良い。

【解答】
$f(x)=x^3-3ax^2+12x+b$ のとき
$f(x)$ が極大値および極小値をとるのは，$f'(x)=0$ が異なる2つの実数解をもつときである。
$x^2-2ax+4=0$ の判別式を $D$ とすると $\dfrac{D}{4}>0$ であるから
よって，求める定数 $a,~b$ が満たすべき条件は