ここでは,指数関数の最大値と最小値に関する問題について説明します。
2次関数に帰着させる問題では定義域に注意しましょう。
また,相加・相乗平均の関係を利用する問題もよく出題されるため,相加・相乗平均の関係の使い方に慣れておきましょう。
Contents
2007年 宮城教育大
2007年 宮城教育大関数 $y=2^{1-2x}-2^{1-x}+1$ を考える。$t=2^{-x}$ とおくことにより,$0\leqq x\leqq2$ のときの最大値と最小値,およびそのときの $x$ の値を求めよ。
【考え方と解答】
$t=2^{-x}$ とおくとき,$x$ が増加すると $t$ は減少するから $0\leqq x\leqq2$ のとき,
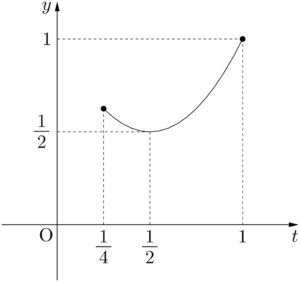
グラフより,$t=1$ のとき $y$ は最大値をとり,$t=\dfrac{1}{2}$ のとき $y$ は最小値をとる。
$t=1$ のとき
$t=2^{-x}$ とおくとき,$x$ が増加すると $t$ は減少するから $0\leqq x\leqq2$ のとき,
\begin{align*}
&2^{-2}\leqq2^x\leqq2^0 \\[4pt]
&\dfrac{1}{4}\leqq t\leqq1
\end{align*}
$y$ を $t$ で表す。&2^{-2}\leqq2^x\leqq2^0 \\[4pt]
&\dfrac{1}{4}\leqq t\leqq1
\end{align*}
\begin{align*}
&2^{1-2x}=2\Cdota(2^{-x})^2=2t^2 \\[4pt]
&2^{1-x}=2\Cdota2^{-x}=2t
\end{align*}
であるから&2^{1-2x}=2\Cdota(2^{-x})^2=2t^2 \\[4pt]
&2^{1-x}=2\Cdota2^{-x}=2t
\end{align*}
\begin{align*}
y&=2t^2-2t+1 \\[4pt]
&=2\left(t-\dfrac{1}{2}\right)^2+\dfrac{1}{2}
\end{align*}
y&=2t^2-2t+1 \\[4pt]
&=2\left(t-\dfrac{1}{2}\right)^2+\dfrac{1}{2}
\end{align*}

グラフより,$t=1$ のとき $y$ は最大値をとり,$t=\dfrac{1}{2}$ のとき $y$ は最小値をとる。
$t=1$ のとき
\begin{align*}
&2^{-x}=1 \\[4pt]
&x=0
\end{align*}
また,$t=\dfrac{1}{2}$ のとき&2^{-x}=1 \\[4pt]
&x=0
\end{align*}
\begin{align*}
&2^{-x}=\dfrac{1}{2} \\[4pt]
&-x=-1 \\[4pt]
&x=1
\end{align*}
よって,$x=0$ のとき $y$ は最大値1をとり,$x=1$ のとき $y$ は最小値 $\dfrac{1}{2}$ をとる。&2^{-x}=\dfrac{1}{2} \\[4pt]
&-x=-1 \\[4pt]
&x=1
\end{align*}


















