Contents
2020年 同志社女子大
2020年 同志社女子大$a$ は定数とし,$f(x)=4^x-5\Cdot2^{x+1}+a+14$ とする。$0\leqq x\leqq3$ における $f(x)$ の最大値が7のとき,$a=\myhako$ である。
【考え方と解答】
$2^x=t$ とおくと,$f(x)$ は $t$ の2次関数になる。文字を置き換えたときは,必ず定義域がどうなるかを調べるようにしよう。
$2^x=t$ とおくと,$0\leqq x\leqq3$ のとき,$1\leqq t\leqq8$ である。
グラフより,$t=1$ のとき $g(t)$ は最大となるから,最大値が7となるのは $g(1)=7$ となるときである。
$2^x=t$ とおくと,$f(x)$ は $t$ の2次関数になる。文字を置き換えたときは,必ず定義域がどうなるかを調べるようにしよう。
$2^x=t$ とおくと,$0\leqq x\leqq3$ のとき,$1\leqq t\leqq8$ である。
\begin{align*}
f(x)&=t^2-10t+a+14 \\[4pt]&=(t-5)^2+a-11
\end{align*}
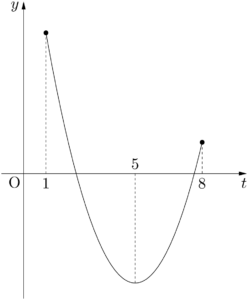
右辺を $g(t)$ とおくと,$y=g(t)$ のグラフは下図のようになる。f(x)&=t^2-10t+a+14 \\[4pt]&=(t-5)^2+a-11
\end{align*}

グラフより,$t=1$ のとき $g(t)$ は最大となるから,最大値が7となるのは $g(1)=7$ となるときである。
\begin{align*}
&16+a-11=7 \\[4pt]&a=2
\end{align*}
よって,$a=2$&16+a-11=7 \\[4pt]&a=2
\end{align*}
2020年 大阪工業大
2020年 大阪工業大$x$ を実数とするとき,$t=2^x+2^{-x}$ のとりうる値の範囲は,$t\geqq\myhako$ である。
また,$f(x)=2^{2x}+2^{-2x}-6(2^x+2^{-x})+3$ の最小値は $\myhako$ である。
また,$f(x)=2^{2x}+2^{-2x}-6(2^x+2^{-x})+3$ の最小値は $\myhako$ である。
【考え方と解答】
誘導があるから,$t$ のとりうる値の範囲を調べることを忘れることはない親切設計の問題である。積が定数になる2つの正の数の和の最小値を求める方法の1つに,相加・相乗平均の関係を利用することがあるのを覚えておこう。
今回は $2^x$ と $2^{-x}$ はともに正の数で,積が1になるから,相加・相乗平均の関係を利用することで最小値を求めることができる。
また,$f(x)$ を $t$ を用いて表すと
グラフより,$f(x)$ は $t=3$ のとき最小値 $-8$ をとる。
誘導があるから,$t$ のとりうる値の範囲を調べることを忘れることはない親切設計の問題である。積が定数になる2つの正の数の和の最小値を求める方法の1つに,相加・相乗平均の関係を利用することがあるのを覚えておこう。
今回は $2^x$ と $2^{-x}$ はともに正の数で,積が1になるから,相加・相乗平均の関係を利用することで最小値を求めることができる。
\begin{align*}
t&=2^x+2^{-x} \\[4pt]&\geqq2\sqrt{2^x\Cdota2^{-x}}=2
\end{align*}
等号が成り立つのは $x=0$ のときであるから,$t\geqq2$ となる。t&=2^x+2^{-x} \\[4pt]&\geqq2\sqrt{2^x\Cdota2^{-x}}=2
\end{align*}
また,$f(x)$ を $t$ を用いて表すと
\begin{align*}
f(x)&=(2^x+2^{-x})^2-2-6(2^x+2^{-x})+3 \\[4pt]&=t^2-6t+1 \\[4pt]&=(t-3)^2-8
\end{align*}
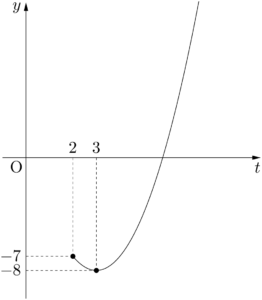
右辺を $g(t)$ とおくと,$y=g(t)$ のグラフは下図のようになる。f(x)&=(2^x+2^{-x})^2-2-6(2^x+2^{-x})+3 \\[4pt]&=t^2-6t+1 \\[4pt]&=(t-3)^2-8
\end{align*}

グラフより,$f(x)$ は $t=3$ のとき最小値 $-8$ をとる。



















