対数螺旋とは,ヒマワリの種が描く螺旋やアンモナイトやオウム貝の殻に現れる螺旋のことで,等角螺旋やベルヌーイの螺旋ともいわれます。
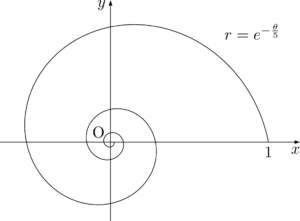
対数螺旋は極方程式で $r=ae^{b\theta}~(a>0)$ と表されます。$a=1,~b=\pm\dfrac{1}{5}$ のときを図示すると次のようになります。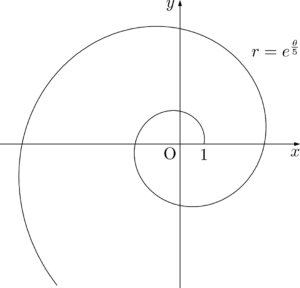
時々入試に出題されるため,グラフの概形,曲線の長さ,等角性,面積などを求める計算に慣れておきましょう。
Contents
対数螺旋の面積

対数螺旋 $r=ae^{b\theta}$ の $\alpha\leqq\theta\leqq\beta$ の部分と2直線 $\theta=\alpha,~\theta=\beta$ で囲まれる部分の面積 $S$ を求めよう。
S&=\dint{\alpha}{\beta}\dfrac{1}{2}r^2\;d\theta \\[4pt]
&=\dint{\alpha}{\beta}\dfrac{a^2}{2}e^{2b\theta}\;d\theta \\[4pt]
&=\dfrac{a^2}{4b}\tint{e^{2b\theta}}{\alpha}{\beta} \\[4pt]
&=\dfrac{a^2}{4b}(e^{2b\beta}-e^{2b\alpha})
\end{align*}
対数螺旋の長さ(弧長)

対数螺旋 $r=ae^{b\theta}$ の $\alpha\leqq\theta\leqq\beta$ の部分の長さ(弧長) $L$ を求めよう。
r’&=abe^{b\theta}
\end{align*}
\left(\dfrac{dx}{d\theta}\right)^2+\left(\dfrac{dy}{d\theta}\right)^2&=(r’)^2+r^2 \\[4pt]
&=(abe^{b\theta})^2+(ae^{b\theta})^2 \\[4pt]
&=a^2(b^2+1)e^{2b\theta}
\end{align*}
L&=\dint{\alpha}{\beta}\sqrt{(r’)^2+r^2}\;d\theta \\[4pt]
&=\dint{\alpha}{\beta}a\sqrt{b^2+1}e^{b\theta}\;d\theta \\[4pt]
&=\dfrac{a\sqrt{b^2+1}}{b}\tint{e^{b\theta}}{\alpha}{\beta} \\[4pt]
&=\dfrac{a\sqrt{b^2+1}}{b}(e^{b\alpha}-e^{b\beta})
\end{align*}
対数螺旋に関する入試問題【2018年 岐阜大】

実際に岐阜大で出題された入試問題を解いてみよう。
r=e^{a\theta}~(0\leqq\theta\leqq\pi)
\end{align*}
(1) $x,~y$ を $\theta$ を用いてそれぞれ表せ。
(2) 曲線 $C$ の長さを求めよ。
(3) 点Pにおける曲線 $C$ の接線の方程式を $\theta$ を用いて表せ。ただし,$0<\theta<\pi$ とする。
(4) 曲線 $C$ 上の点Pと原点を通る直線を $l$,点Pにおける曲線 $C$ の接線を $m$ とする。$l$ と $m$ のなす角はPによらず一定であることを示せ。
(5) $l$ と $m$ のなす角が $\dfrac{\pi}{12}$ となるような $a$ の値を求めよ。

(1)は次のポイントを利用しよう。
x=r\cos\theta,~~y=r\sin\theta
\end{align*}
$r=e^{a\theta}$ より
&x=r\cos\theta=e^{a\theta}\cos\theta \\[4pt]
&y=r\sin\theta=e^{a\theta}\sin\theta
\end{align*}

曲線の長さを求める公式を利用しよう。
\dfrac{dx}{d\theta}&=ae^{a\theta}\cos\theta-e^{a\theta}\sin\theta \\[4pt]
&=e^{a\theta}(a\cos\theta-\sin\theta) \\[4pt]
\dfrac{dy}{d\theta}&=ae^{a\theta}\sin\theta+e^{a\theta}\cos\theta \\[4pt]
&=e^{a\theta}(a\sin\theta+\cos\theta)
\end{align*}
\left(\dfrac{dx}{d\theta}\right)^2+\left(\dfrac{dy}{d\theta}\right)^2
&=e^{2a\theta}(a\cos\theta-\sin\theta)^2+e^{2a\theta}(a\sin\theta+\cos\theta)^2 \\[4pt]
&=e^{2a\theta}(a^2+1)
\end{align*}
L&=\dint{0}{\pi}\sqrt{\left(\dfrac{dx}{d\theta}\right)^2+\left(\dfrac{dy}{d\theta}\right)^2}\;d\theta \\[4pt]
&=\dint{0}{\pi}e^{a\theta}\sqrt{a^2+1}\;d\theta \\[4pt]
&=\sqrt{a^2+1}\Tint{\dfrac{1}{a}e^{a\theta}}{0}{\pi} \\[4pt]
&=\dfrac{\sqrt{a^2+1}}{a}(e^{a\pi}-1)
\end{align*}

媒介変数表示されているから,ベクトルで考えよう。
b(x-p)-a(y-q)=0
\end{align*}
点Pの接線 $m$ の方向ベクトルを $\vec{m}$ とすると
\vec{m}=(a\cos\theta-\sin\theta,~a\sin\theta+\cos\theta)
\end{align*}
&(a\sin\theta+\cos\theta)(x-e^{a\theta}\cos\theta)-(a\cos\theta-\sin\theta)(y-e^{a\theta}\sin\theta)=0 \\[4pt]
&(a\sin\theta+\cos\theta)x-(a\cos\theta-\sin\theta)y-e^{a\theta}(\cos^2\theta+\sin^2\theta)=0 \\[4pt]
&(a\sin\theta+\cos\theta)x-(a\cos\theta-\sin\theta)y-e^{a\theta}=0
\end{align*}

ベクトルを利用しないと,ちょっと面倒なことになる。
k=\dfrac{a\sin\theta+\cos\theta}{a\cos\theta-\sin\theta}
\end{align*}

(3)を解くときにベクトルで考えた人は,(4)もベクトルで考えるだろう。(3)でベクトルで考えなかった人は,(4)でもベクトルを利用せず,三角関数の $\tan$ の加法定理を利用して考えるのだろう。ベクトルを1つの道具として使えるようになろう。
直線 $l$ の方向ベクトルを $\vec{\ell}$ とすると,
\vec{\ell}=(\cos\theta,~\sin\theta),~~\abs{\vec{\ell}}=1
\end{align*}
\abs{\vec{m}}&=\sqrt{(a\cos\theta-\sin\theta)^2+(a\sin\theta+\cos\theta)^2} \\[4pt]
&=\sqrt{a^2+1}
\end{align*}
\cos\phi&=\dfrac{\vec{\ell}\Cdot\vec{m}}{\abs{\vec{\ell~}}\abs{\vec{m}}} \\[4pt]
&=\dfrac{(a\cos\theta-\sin\theta)\cos\theta+(a\sin\theta+\cos\theta)\sin\theta}{\sqrt{a^2+1}} \\[4pt]
&=\dfrac{a}{\sqrt{a^2+1}}
\end{align*}
よって,$l$ と $m$ のなす角はPによらず一定である。

(4)で $\cos\phi$ を $a$ で表しているから,$\cos\dfrac{\pi}{12}$ の値を求めれば $a$ の方程式を立てることができる。

ただ,(4)の式には根号があるため,2乗することを考えると,$\cos^2\dfrac{\pi}{12}$ を求めた方が良いね。

目の前のものにすぐ飛びつくのではなく,一つ先を考えて,「本当に必要なものは何なのか」を落ち着いて考えるようにしよう。
\cos^2\dfrac{\pi}{12}&=\dfrac{1+\cos\frac{\pi}{6}}{2} \\[4pt]
&=\dfrac{2+\sqrt{3}}{4}
\end{align*}
&\cos^2\dfrac{\pi}{12}=\dfrac{a^2}{a^2+1} \\[4pt]
&\dfrac{2+\sqrt{3}}{4}=\dfrac{a^2}{a^2+1} \\[4pt]
&(2+\sqrt{3})(a^2+1)=4a^2 \\[4pt]
&a^2=\dfrac{2+\sqrt{3}}{2-\sqrt{3}}=(2+\sqrt{3})^2
\end{align*}
対数螺旋に関する入試問題2【2018年 東京理科大】

もう1問,東京理科大で出題された問題を解いてみよう。
\begin{cases}
x=e^{-\theta}\cos\theta \\[4pt]
y=e^{-\theta}\sin\theta
\end{cases}
\end{align*}
(1) 曲線 $C_1$ の $x$ 軸との交点の $x$ 座標は $\myhako$ であり,$y$ 軸との交点の $y$ 座標は $\myhako$ である。また,関数 $e^{-\theta}\cos\theta~\left(\dfrac{\pi}{4}\leqq\theta\leqq\dfrac{5\pi}{4}\right)$ は $\theta=\myhako$ で極値 $\myhako$ をとる。
(2) 曲線 $C_1$ と $C_2$ によって囲まれる図形のうち,$x$ 座標が $x\leqq0$ を満たす部分の面積は $\myhako$ である。

座標軸との交点については大丈夫だろう。
$x$ 軸上の点は $y$ 座標が0であるから
e^{-\theta}\sin\theta=0
\end{align*}
$\dfrac{\pi}{4}\leqq\theta\leqq\dfrac{5\pi}{4}$ より $\theta=\pi$
よって,$x$ 軸との交点の $x$ 座標は $e^{-\pi}\cos\pi=-e^{-\pi}$
$y$ 軸上の点は $x$ 座標が0であるから
e^{-\theta}\cos\theta=0
\end{align*}
$\dfrac{\pi}{4}\leqq\theta\leqq\dfrac{5\pi}{4}$ より $\theta=\dfrac{\pi}{2}$
よって,$y$ 軸との交点の $y$ 座標は $e^{-\frac{\pi}{2}}\sin\dfrac{\pi}{2}=e^{-\frac{\pi}{2}}$

微分して増減表を書いて極値を求めよう。
$f(\theta)=e^{-\theta}\cos\theta$ とおくと
f'(\theta)&=-e^{-\theta}\cos\theta-e^{-\theta}\sin\theta \\[4pt]
&=-e^{-\theta}(\cos\theta+\sin\theta) \\[4pt]
&=-\sqrt{2}e^{-\theta}\sin\left(\theta+\dfrac{\pi}{4}\right)
\end{align*}
&\sin\left(\theta+\dfrac{\pi}{4}\right)=0
\end{align*}
&\theta+\dfrac{\pi}{4}=\pi \\[4pt]
&\theta=\dfrac{3}{4}\pi
\end{align*}
\begin{array}{|c||c|c|c|c|c|}\hline
\theta & \dfrac{\pi}{4} & \cdots & \dfrac{3}{4}\pi & \cdots & \dfrac{5}{4}\pi \\\hline
f'(\theta) & & – & 0 & + & \\\hline
f(\theta) & & \searrow & -\dfrac{1}{\sqrt{2}}e^{-\frac{3}{4}\pi} & \nearrow & \\\hline
\end{array}
\end{align*}

まずは考えている図形を図示しよう。
$g(\theta)=e^{-\theta}\sin\theta$ とすると
g'(\theta)&=-e^{-\theta}\sin\theta+e^{-\theta}\cos\theta \\[4pt]
&=\sqrt{2}e^{-\theta}\sin\left(\theta+\dfrac{3}{4}\pi\right)
\end{align*}
\sin\left(\theta+\dfrac{3}{4}\pi\right)\leqq0
\end{align*}
したがって,図の斜線部分の面積が求める面積 $S$ である。
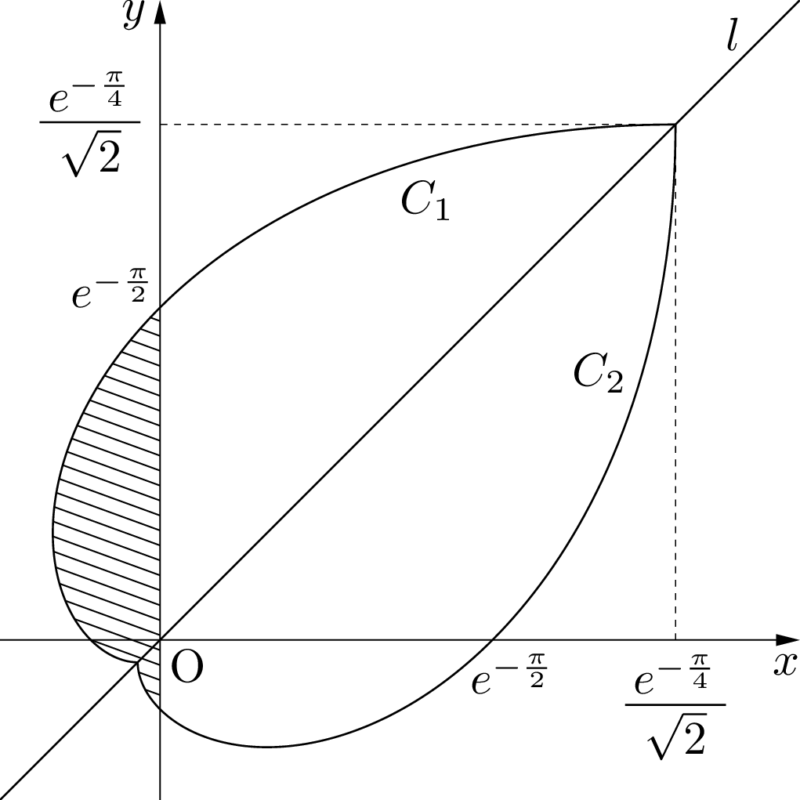
次の図のように赤い部分の面積を $S_1$,青い部分の面積を $S_2$ とすると
S=S_1+2S_2
\end{align*}

極方程式における面積公式より
S_1&=\dint{\frac{\pi}{2}}{\pi}\dfrac{1}{2}e^{-2\theta}\;d\theta \\[4pt]
&=-\dfrac{1}{4}\tint{e^{-2\theta}}{\frac{\pi}{2}}{\pi} \\[4pt]
&=\dfrac{1}{4}(e^{-\pi}-e^{-2\pi}) \\[4pt]
S_2&=\dint{\pi}{\frac{5}{4}\pi}\dfrac{1}{2}e^{-2\theta}\;d\theta \\[4pt]
&=-\dfrac{1}{4}\tint{e^{-2\theta}}{\pi}{\frac{5}{4}\pi} \\[4pt]
&=\dfrac{1}{4}\left(e^{-2\pi}-e^{-\frac{5}{2}\pi}\right)
\end{align*}
S&=S_1+2S_2 \\[4pt]
&=\dfrac{1}{4}(e^{-\pi}-e^{-2\pi})+\dfrac{1}{2}\left(e^{-2\pi}-e^{-\frac{5}{2}\pi}\right) \\[4pt]
&=\dfrac{1}{4}(e^{-\pi}+e^{-2\pi}-2e^{-\frac{5}{2}\pi})
\end{align*}
対数螺旋の性質についてのまとめ

対数螺旋(等角螺旋)の性質についてまとめると次のようになる。
- グラフ
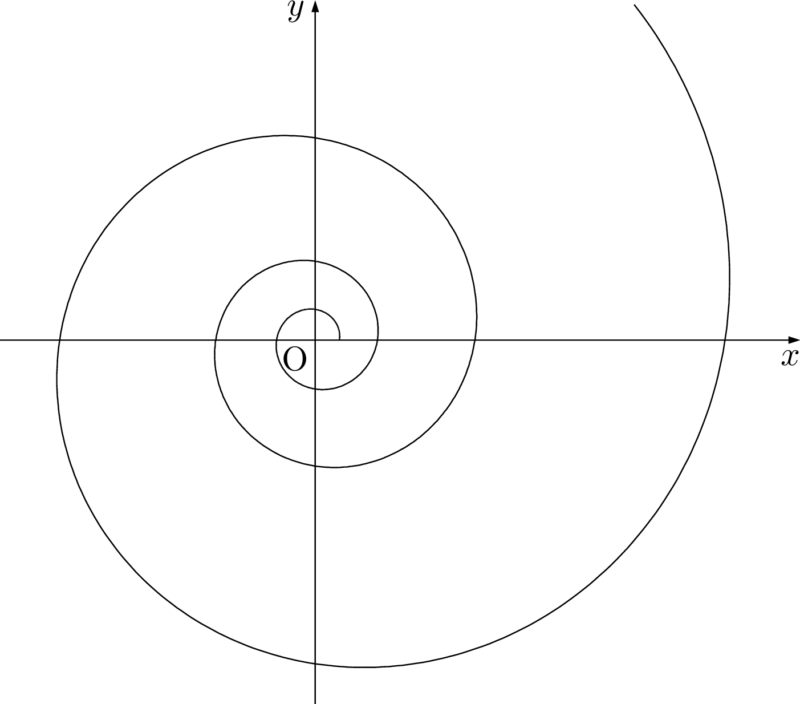
- 媒介変数表示\begin{align*}
x=ae^{b\theta}\cos\theta,~~y=ae^{b\theta}\sin\theta
\end{align*} - 極方程式\begin{align*}
r=ae^{b\theta}
\end{align*} - 面積\begin{align*}
S=\dfrac{a^2}{4b}(e^{2b\beta}-e^{2b\alpha})
\end{align*} - 弧長\begin{align*}
L=\dfrac{a\sqrt{b^2+1}}{b}(e^{b\alpha}-e^{b\beta})
\end{align*} - 等角性
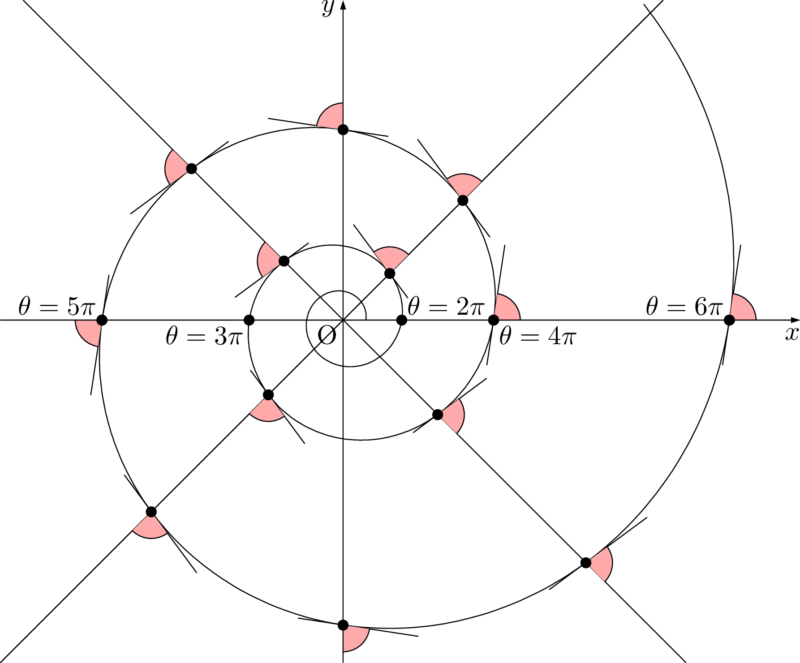
原点から伸ばした半直線と対数螺旋のなす角は一定である。下図において,色を付けた角度はすべて等しい。