Contents
3次関数の最大値と最小値に関する問題
2021年 自治医科大関数 $f(x)=x^3-3ax^2+b$($a,~b$ は実数,$0<a<1$)は,$-1\leqq x\leqq2$($x$ は実数)において,最大値6,最小値0をとるものとする。このときの $\dfrac{b}{a}$ の値を求めよ。
【解答と考え方】
$f(x)=x^3-3ax^2+b$ のとき
$f(0)>f(2)$ のとき
したがって,最小値が0になることはないから,$b\neq6$ である。
$0<a<\dfrac{2}{3}$ のとき,$f(x)$ は $x=2$ で最大値 $-12a+b+8$ をとる。最大値が6であるから,
$f(x)=x^3-3ax^2+b$ のとき
\begin{align*} f'(x)=3x^2-6ax=3x(x-2a) \end{align*}
$f'(x)=0$ を解くと,$x=0,~2a$ $0<a<1$ より,$0<2a<2$ であるから,$f(x)$ の増減は次のようになる。\begin{align*}
\begin{array}{|c||c|c|c|c|c|c|c|}\hline x & -1 & \cdots & 0 & \cdots & 2a & \cdots & 2 \\\hline f'(x) & & + & 0 & – & 0 & + & \\\hline f(x) & & \nearrow & 極大 & \searrow & 極小 & \nearrow & \\\hline \end{array} \end{align*}
ここで $x=-1,~0,~2a,~2$ のときの $f(x)$ の値を求めると次のようになる。\begin{array}{|c||c|c|c|c|c|c|c|}\hline x & -1 & \cdots & 0 & \cdots & 2a & \cdots & 2 \\\hline f'(x) & & + & 0 & – & 0 & + & \\\hline f(x) & & \nearrow & 極大 & \searrow & 極小 & \nearrow & \\\hline \end{array} \end{align*}
\begin{align*} &f(-1)=-3a+b-1 \\[4pt] &f(0)=b \\[4pt] &f(2a)=-4a^3+b \\[4pt] &f(2)=-12a+b+8 \end{align*}
最大値は $f(0)$ と $f(2)$ のうち大きい方であるが,$a$ の値によって,大小関係が変わるかもしれないと思ったら,1つずつ調べよう。$f(0)>f(2)$ のとき
\begin{align*}
&b>-12a+b+8 \\[4pt]
&12a>8 \\[4pt]
&a>\dfrac{2}{3}
\end{align*}
つまり,$\dfrac{2}{3}<a<1$ のとき,$f(x)$ は $x=0$ で最大値 $b$ をとる。最大値が6であるから,$b=6$ 次に最小値を調べる。このとき&b>-12a+b+8 \\[4pt]
&12a>8 \\[4pt]
&a>\dfrac{2}{3}
\end{align*}
\begin{align*} &f(-1)=-3a+5 \\[4pt] &f(2a)=-4a^3+6 \end{align*}
ここで $0<a<1$ のとき,$-4a^3+6>2$ となるから,$f(2a)=0$ となることはない。同様に,$-3a+5>2$ となるから,$f(-1)=0$ となることもない。したがって,最小値が0になることはないから,$b\neq6$ である。
$0<a<\dfrac{2}{3}$ のとき,$f(x)$ は $x=2$ で最大値 $-12a+b+8$ をとる。最大値が6であるから,
\begin{align*} &-12a+b+8=6 \\[4pt] &b=12a-2 \end{align*}
このとき\begin{align*} &f(-1)=9a-3 \\[4pt] &f(2a)=-4a^3+12a-2 \end{align*}
であり, \begin{align*} f(-1)-f(2a)&=4a^3-3a-1 \\[4pt] &=(a-1)(4a^2+4a+1) \\[4pt] &=(a-1)(2a+1)^2 \end{align*}
$0<a<1$ のとき,$f(-1)-f(2a)<0$ となるから,$f(x)$ は $x=-1$ で最小値をとる。最小値が0であるから\begin{align*} &f(-1)=9a-3=0 \\[4pt] &a=\dfrac{1}{3} \end{align*}
このとき \begin{align*} b=12\Cdota\dfrac{1}{3}-2=2 \end{align*}
したがって,求める $\dfrac{b}{a}$ の値は\begin{align*} \dfrac{b}{a}=\dfrac{2}{\dfrac{1}{3}}=6 \end{align*}

ヒロ
ちなみに,3次関数の対称性を利用してグラフを描いて考えると,最小値をとる $x$ の値がすぐに分かる。
長方形を8等分したものを描くと,$x^3$ の係数が正の3次関数のグラフは5個の黒丸を通る。
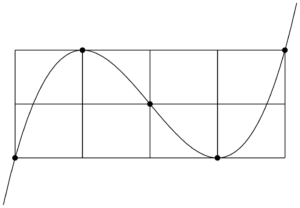
最小値が0であるから,長方形の底辺と重なる位置に $x$ 軸がある。$x$ 軸の位置が分からない場合は,適当に描いておけばよい。
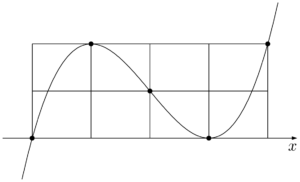
$f'(x)=0$ を解くと,$x=0,~2a$ となるから,次のようになっていることが分かる。
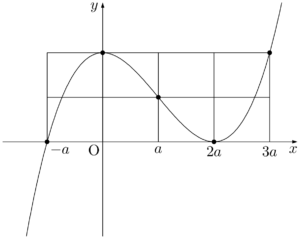
$0<a<1$ より,$-1<-a$ であるから,直線 $x=-1$ を描き加えると次のようになる。
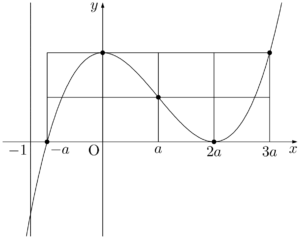
これによって,$x=-1$ で最小値をとることが分かる。
直線 $x=2$ は $x>2a$ の部分にあるから,$2a<2<3$ のときと $3a<2$ のときで場合分けして考えればよい。

ヒロ
3次関数の等間隔性を利用する解法については,次の記事で入試問題を用いて解説している。



















