図形の性質の考え方・解き方の第四弾です。第一弾~第三弾は有名三角形を扱ってきましたが,ここでは三角比の値が与えられたときの描画について説明します。
三角比の値が与えられたときの図を描く方法を身に付けることで,出題者が最初に描いた図を描くことができる場合があります。
センター試験の数学IAの図形問題の考え方を説明します。
\mathrm{AB=2\sqrt3,~AC=3},~\cos C=\dfrac{\sqrt6}{3}
\end{align*}
\dfrac{\myBox{カ}\sqrt{2}+\myBox{キ}\sqrt{3}}{2}
\end{align*}
通常解法

まずはよくある解法で解いておこう。

とりあえず図を描くんですよね。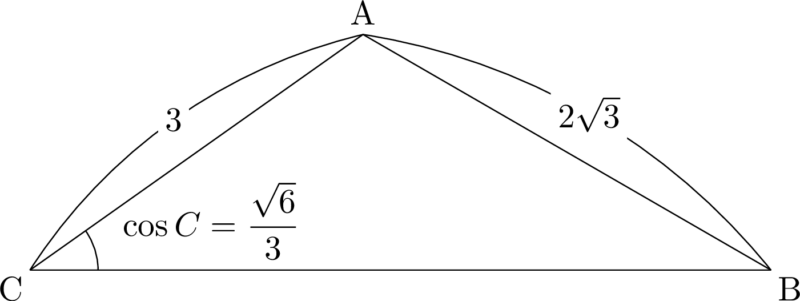

$\sin B$ を求める問題で,対辺ACの長さが分かっているということはどうする?

$C$ の対辺ABの長さが分かっているから,正弦定理で求められますね。
\sin C&=\sqrt{1-\cos^2C} \\[4pt]
&=\sqrt{1-\left(\dfrac{\sqrt{6}}{3}\right)^2} \\[4pt]
&=\dfrac{\sqrt{3}}{3}
\end{align*}
&\mathrm{AC}\sin C=\mathrm{AB}\sin B \\[4pt]
&3\Cdota\dfrac{\sqrt{3}}{3}=2\sqrt{3}\sin B \\[4pt]
&\sin B=\dfrac{1}{2}
\end{align*}

次は外接円の半径を求めよう。

外接円の半径ときたら正弦定理ですね!
2R&=\dfrac{\mathrm{AC}}{\sin B} \\[4pt]
&=\dfrac{3}{\dfrac{1}{2}} \\[4pt]
&=6
\end{align*}

次はBCの長さを求めよう。

$\cos C$ が分かっているから余弦定理を使えばいいのかな・・・
&\mathrm{AB}^2=\mathrm{BC}^2+\mathrm{AC}^2-2\mathrm{BC}\Cdota\mathrm{AC}\cos C \\[4pt]
&(2\sqrt{3})^2=\mathrm{BC}^2+3^2-2\mathrm{BC}\Cdota3\Cdota\dfrac{\sqrt{6}}{3} \\[4pt]
&\mathrm{BC}^2-2\sqrt{6}\mathrm{BC}-3=0 \\[4pt]
&\mathrm{BC}=\sqrt{6}\pm3
\end{align*}

なんとか求まったね。最後の $\sankaku{ABC}$ の面積を求めよう。

三角形の面積公式で簡単に求められますね。
S&=\dfrac{1}{2}(\sqrt{6}+3)\Cdota2\sqrt{3}\Cdota\dfrac{1}{2} \\[4pt]
&=\dfrac{3\sqrt{2}+3\sqrt{3}}{2}
\end{align*}
$\cos$ の値を利用して図を描く方法

さて,ここからが本番だ。最初に図を描くときに,ちゃんと三角比の値を利用して図を描こう。今回の場合,$\cos C=\dfrac{\sqrt{6}}{3}$ を利用して,できるだけ正確な図を描こう。

まず,斜辺が3で底辺が $\sqrt{6}~(\fallingdotseq 2.4)$ の直角三角形を描く。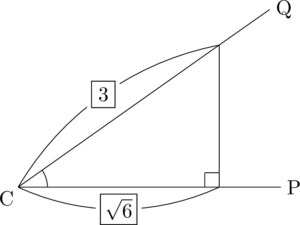

2点A, BはCP上とCQ上にある。どちらの点をどちらの辺上にとるかは,与えられている辺の長さで決めよう。

今回は比の $\fbox{3}$ とACの長さが一致しているから,斜辺上にAをとる。そうすることで比として書いた値がそのまま長さになる。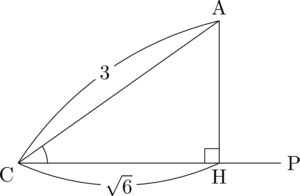

残りの点BはCP上にある。ここで,三平方の定理を使ってAHの長さを求めると,$\mathrm{AH}=\sqrt3$ となる。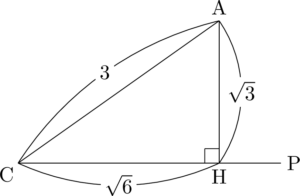

$\mathrm{AB}=2\sqrt3$ だからAHの2倍の長さになるようにCP上に点Bをとることを考える。ここで $\mathrm{AC}=3$ より,ABがACより長いため,点Bは辺CH上にはとることはできない。したがって,点Bを点Hより右側にとることになる。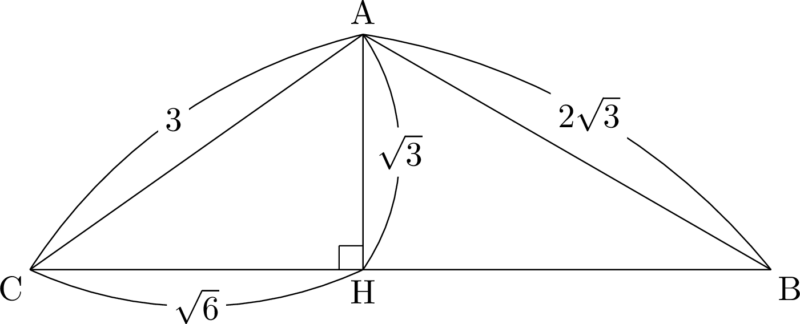

$\cos C=\dfrac{\sqrt{6}}{3}$ をちゃんと利用して描けば,最初からここまで描くことができる。この時点で分かることをさらに書き込もう。

三平方の定理から $\mathrm{BH}=3$ となりますね。というか,$\sankaku{ABH}$ って $1:2:\sqrt3$ の三角定規の三角形じゃないですか!角度も分かりますね。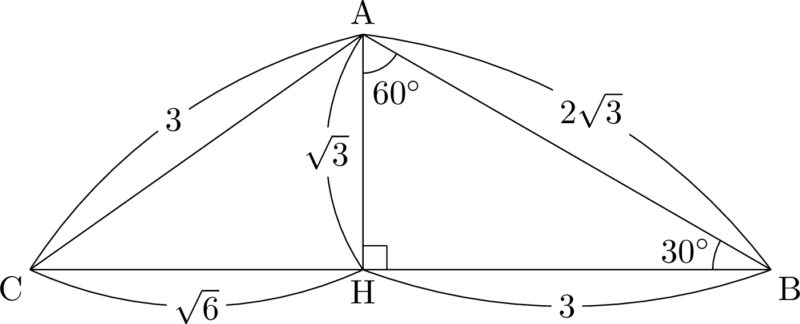

そうだね。それでは,この図を見て問題を解いていこう。
図を描くだけで既に解いている

まずは $\sin B$ の値を求めよう。

$B=30\Deg$ って分かってるので,さっきみたいに計算しなくても $\sin B=\dfrac{1}{2}$ って出ますね。

そうだね。次は外接円の半径を求めよう。正弦定理を使うのは変わらないけど,正弦定理の公式の覚え方を少し変えよう。
R=\dfrac{3}{2\sin30\Deg}=3
\end{align*}

教科書には $2R=\dfrac{a}{\sin A}$ の形で載ってるけど,$R=\dfrac{a}{2\sin A}$ の形で使えるようにしよう。ほとんどの問題では半径を求めるわけで,三角定規の有名角(30°,45°,60°,120°,135°,150°)の場合は $\sin A$ の前に2があることで分母が分数になるのを避けることもできる。たまに出題される直径を求める問題では,今まで通り $2R=$ の式を使えば良い。

それでは次のBCの長さを求めよう。

BCの長さってもう出てますね。空欄の順だと $\mathrm{BC}=3+\sqrt{6}$ です。

ちなみに,さっきは余弦定理を使ってBCの長さを求めたけど,余弦定理には2種類あるからね。

普段使っている余弦定理は「第二余弦定理」というもので,もう1つ「第一余弦定理」がある。
$\sankaku{ABC}$ の頂点Cから底辺ABに垂線AHを下ろした図を考えよう。
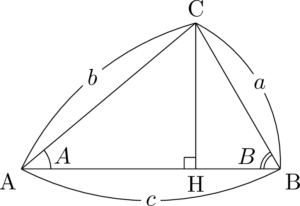

$\sankaku{ACH}$ に着目すると
\mathrm{AH}=b\cos A
\end{align*}
\mathrm{BH}=a\cos B
\end{align*}
c=b\cos A+a\cos B
\end{align*}

今回の問題で第一余弦定理を使ってBCの長さを求めると次のようになる。
\mathrm{BC}&=\mathrm{AC}\cos C+\mathrm{AB}\cos B \\[4pt]
&=3\Cdota\dfrac{\sqrt{6}}{3}+2\sqrt{3}\Cdota\dfrac{\sqrt{3}}{2} \\[4pt]
&=\sqrt{6}+3
\end{align*}
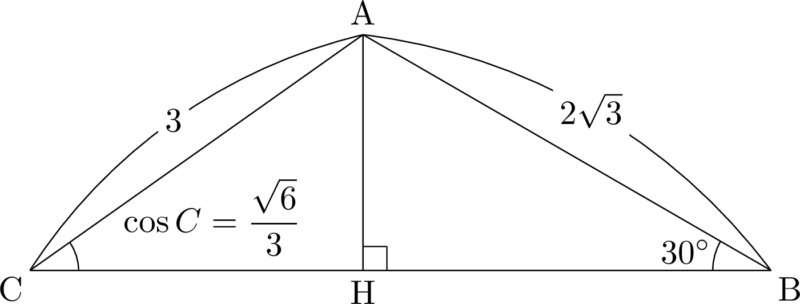

じゃあ最後の $\sankaku{ABC}$ の面積を求めよう。

底辺も高さも分かってるから簡単ですね。
S&=\dfrac{1}{2}(\sqrt{6}+3)\Cdota\sqrt{3} \\[4pt]
&=\dfrac{3\sqrt{2}+3\sqrt{3}}{2}
\end{align*}
2003年センターIA図形を解いた感想

与えられた三角比の値を利用して,できるだけ正確な図を描くことによって,計算量をかなり減らすことができた。

また,与えられた条件を見ただけで,出題者が最初に描いたであろう図を描くこともできた。図を描いた時点で,問題文を読む前に,辺の長さや角の大きさを求めることができたため,かなり時間短縮することができた。




















