放物線と2本の接線で囲まれた部分の面積を求める方法を説明します。
一般的には「12分の1公式」と呼ばれる公式を利用することで,放物線と接線で囲まれた部分の面積を簡単に求めることができます。
具体的な問題を通して,12分の1公式の使い方などを学びましょう。
12分の1公式

ヒロ
12分の1公式の証明については,次の記事で説明しているため,ここでは省略する。
2021年 愛知工業大
2021年 愛知工業大$xy$ 平面において,点 $\left(0,~\dfrac{5}{4}\right)$ から放物線 $y=1-x^2$ に引いた2本の接線の方程式は $\myhako$ である。また,放物線とこの2本の接線で囲まれた部分の面積は $\myhako$ である。

ヒロ
答えを求めることのみを追求した場合は次のように求めることができる。
【解答】
接点の $x$ 座標を $t$ とすると
接点の $x$ 座標を $t$ とすると
\begin{align*}
&t^2=\dfrac{5}{4}-1 \\[4pt]
&t^2=\dfrac{1}{4} \\[4pt]
&t=\pm\dfrac{1}{2}
\end{align*}
接点の座標は $\left(\pm\dfrac{1}{2},~\dfrac{3}{4}\right)$ となるから,接線の傾きは&t^2=\dfrac{5}{4}-1 \\[4pt]
&t^2=\dfrac{1}{4} \\[4pt]
&t=\pm\dfrac{1}{2}
\end{align*}
\begin{align*}
\dfrac{\dfrac{3}{4}-\dfrac{5}{4}}{\pm\dfrac{1}{2}-0}=\mp1
\end{align*}
よって,2本の接線の方程式は\dfrac{\dfrac{3}{4}-\dfrac{5}{4}}{\pm\dfrac{1}{2}-0}=\mp1
\end{align*}
\begin{align*}
y=\pm x+\dfrac{5}{4}
\end{align*}
2接点の $x$ 座標の差は1であるから,求める面積はy=\pm x+\dfrac{5}{4}
\end{align*}
\begin{align*}
\dfrac{1}{12}\Cdota1^3=\dfrac{1}{12}
\end{align*}
\dfrac{1}{12}\Cdota1^3=\dfrac{1}{12}
\end{align*}

ヒロ
接点の $x$ 座標をどのようにして求めているかを理解したい人は,次の記事を読むと解決するだろう。

ヒロ
ちゃんと(?)考えると次のようになる。
【解答と考え方】
接点の $x$ 座標を $t$ とする。$y=1-x^2$ のとき,$y’=-2x$ であるから,接線の方程式は

$y$ 軸に関して対称であることを考えると
接点の $x$ 座標を $t$ とする。$y=1-x^2$ のとき,$y’=-2x$ であるから,接線の方程式は
\begin{align*}
&y=-2t(x-t)+1-t^2 \\[4pt]
&y=-2tx+t^2+1
\end{align*}
これが点 $\left(0,~\dfrac{5}{4}\right)$ を通るから&y=-2t(x-t)+1-t^2 \\[4pt]
&y=-2tx+t^2+1
\end{align*}
\begin{align*}
&\dfrac{5}{4}=t^2+1 \\[4pt]
&t^2=\dfrac{1}{4} \\[4pt]
&t=\pm\dfrac{1}{2}
\end{align*}
したがって,2本の接線の方程式は次のようになる。&\dfrac{5}{4}=t^2+1 \\[4pt]
&t^2=\dfrac{1}{4} \\[4pt]
&t=\pm\dfrac{1}{2}
\end{align*}
\begin{align*}
y=\pm x+\dfrac{5}{4}
\end{align*}
求める面積 $S$ は図の色を塗った部分の面積である。y=\pm x+\dfrac{5}{4}
\end{align*}

$y$ 軸に関して対称であることを考えると
\begin{align*}
S&=2\dint{0}{\frac{1}{2}}\left\{-x+\dfrac{5}{4}-(1-x^2)\right\}\;dx \\[4pt]
&=2\dint{0}{\frac{1}{2}}\left(x-\dfrac{1}{2}\right)^2\;dx \\[4pt]
&=2\Tint{\dfrac{1}{3}\left(x-\dfrac{1}{2}\right)^3}{0}{\frac{1}{2}} \\[4pt]
&=\dfrac{2}{3}\Cdota\dfrac{1}{8} \\[4pt]
&=\dfrac{1}{12}
\end{align*}
S&=2\dint{0}{\frac{1}{2}}\left\{-x+\dfrac{5}{4}-(1-x^2)\right\}\;dx \\[4pt]
&=2\dint{0}{\frac{1}{2}}\left(x-\dfrac{1}{2}\right)^2\;dx \\[4pt]
&=2\Tint{\dfrac{1}{3}\left(x-\dfrac{1}{2}\right)^3}{0}{\frac{1}{2}} \\[4pt]
&=\dfrac{2}{3}\Cdota\dfrac{1}{8} \\[4pt]
&=\dfrac{1}{12}
\end{align*}
2021年 甲南大
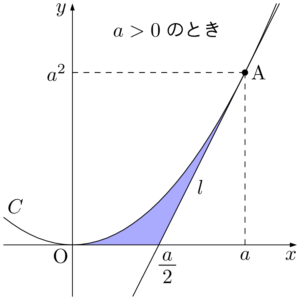
2021年 甲南大座標平面において,放物線 $C:y=x^2$ および $C$ 上の点A$(a,~a^2)$ が与えられている。ただし,$a\neq0$ とする。Aにおける $C$ における接線を $l$ として,以下の問いに答えよ。
(1) $l$ の方程式を求めよ。
(2) $C$ と $x$ 軸と $l$ とで囲まれた部分の面積を求めよ。
(1) $l$ の方程式を求めよ。
(2) $C$ と $x$ 軸と $l$ とで囲まれた部分の面積を求めよ。
【(1)の解答と考え方】
$y=x^2$ のとき,$y’=2x$ であるから,点Aにおける接線 $l$ の方程式は次のようになる。
$y=x^2$ のとき,$y’=2x$ であるから,点Aにおける接線 $l$ の方程式は次のようになる。
\begin{align*}
&y=2a(x-a)+a^2 \\[4pt]
&y=2ax-a^2
\end{align*}
&y=2a(x-a)+a^2 \\[4pt]
&y=2ax-a^2
\end{align*}
(2) $C$ と $x$ 軸と $l$ とで囲まれた部分の面積を求めよ。
【(2)の解答と考え方】
$l$ と $x$ 軸の交点を求める。
ここで,$x$ 軸が $C$ の接線であることを考えると,12分の1公式を利用できることが分かる。2つの接点の $x$ 座標の差は $a$ であるから,
記述式の試験で12分の1公式を使って値を求めて減点されるのではないかと思う人は,しっかり書いておけば良い。ただ,
$l$ と $x$ 軸の交点を求める。
\begin{align*}
&2ax-a^2=0 \\[4pt]
&a(2x-a)=0 \\[4pt]
&x=\dfrac{a}{2}
\end{align*}
求める面積を $S$ とすると,図の色を塗った部分の面積が $S$ である。&2ax-a^2=0 \\[4pt]
&a(2x-a)=0 \\[4pt]
&x=\dfrac{a}{2}
\end{align*}


ここで,$x$ 軸が $C$ の接線であることを考えると,12分の1公式を利用できることが分かる。2つの接点の $x$ 座標の差は $a$ であるから,
\begin{align*}
S=\dfrac{1}{12}\abs{a}^3
\end{align*}
となる。S=\dfrac{1}{12}\abs{a}^3
\end{align*}
記述式の試験で12分の1公式を使って値を求めて減点されるのではないかと思う人は,しっかり書いておけば良い。ただ,
\begin{align*}
x^2-(2ax-a^2)=(x-a)^2
\end{align*}
となることは,計算しなくても分かるようにしておくべきである。$a>0$ のときx^2-(2ax-a^2)=(x-a)^2
\end{align*}
\begin{align*}
S&=\dint{0}{\frac{a}{2}}x^2\;dx+\dint{\frac{a}{2}}{a}(x-a)^2\;dx \\[4pt]
&=\Tint{\dfrac{1}{3}x^3}{0}{\frac{a}{2}}+\Tint{\dfrac{1}{3}(x-a)^3}{\frac{a}{2}}{a} \\[4pt]
&=\dfrac{1}{3}\Cdota\dfrac{a^3}{8}+\dfrac{1}{3}\Cdota\dfrac{a^3}{8} \\[4pt]
&=\dfrac{1}{12}a^3
\end{align*}
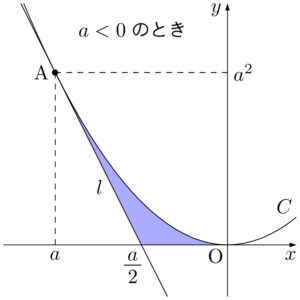
$a<0$ のときS&=\dint{0}{\frac{a}{2}}x^2\;dx+\dint{\frac{a}{2}}{a}(x-a)^2\;dx \\[4pt]
&=\Tint{\dfrac{1}{3}x^3}{0}{\frac{a}{2}}+\Tint{\dfrac{1}{3}(x-a)^3}{\frac{a}{2}}{a} \\[4pt]
&=\dfrac{1}{3}\Cdota\dfrac{a^3}{8}+\dfrac{1}{3}\Cdota\dfrac{a^3}{8} \\[4pt]
&=\dfrac{1}{12}a^3
\end{align*}
\begin{align*} S&=\dint{a}{\frac{a}{2}}(x-a)^2\;dx+\dint{\frac{a}{2}}{0}x^2\;dx \\[4pt] &=-\dfrac{1}{12}a^3 \end{align*}

ヒロ
放物線と直線が接する場合,2つの関数の差を因数分解すると「2乗の形」になる。できれば2乗の形のまま,積分できるようにした方が良い。累乗の形の積分公式については,次の記事に載せている。





















