Contents
分数式の加法と減法の入試問題
2015年 広島国際学院大次の式を簡単にしなさい。
\begin{align*}
\dfrac{x^2}{x-2}-\dfrac{4}{x-2}-1
\end{align*}
\dfrac{x^2}{x-2}-\dfrac{4}{x-2}-1
\end{align*}
【考え方と解答】
分母を $x-2$ に揃えて計算しよう。
分母を $x-2$ に揃えて計算しよう。
\begin{align*}
(与式)&=\dfrac{x^2-4-(x-2)}{x-2} \\[4pt]
&=\dfrac{x^2-x-2}{x-2} \\[4pt]
&=\dfrac{(x-2)(x+1)}{x-2} \\[4pt]
&=x+1
\end{align*}
(与式)&=\dfrac{x^2-4-(x-2)}{x-2} \\[4pt]
&=\dfrac{x^2-x-2}{x-2} \\[4pt]
&=\dfrac{(x-2)(x+1)}{x-2} \\[4pt]
&=x+1
\end{align*}

ヒロ
今回の問題では,前の2項を見て「$x^2-4=(x+2)(x-2)$」が想像した人は,最後の $-1$ まで通分する必要はないと分かるね。
【別解】
\begin{align*}
(与式)&=\dfrac{x^2-4}{x-2}-1 \\[4pt]
&=(x+2)-1=x+1
\end{align*}
(与式)&=\dfrac{x^2-4}{x-2}-1 \\[4pt]
&=(x+2)-1=x+1
\end{align*}
分数式の加法と減法の入試問題2
2009年 広島工業大$\dfrac{1}{x^2-4}-\dfrac{1}{x^2-2x}$ を計算すると $\dfrac{\myhako}{x(x^2-4)}$ となる。
【考え方と解答】
通分することを考えるが,分母を見て「$(x^2-4)(x^2-2x)$」で通分すると「答えの形」と一致しないと思って諦める人がいるが,諦めずに手を動かしてほしい。
$x^2-2x$ は $x(x-2)$ と因数分解できるのだから,計算した結果「$x-2$ が約分で消えるのかなぁ」と思えれば,白紙にはならないだろう。また,$x^2-4=(x+2)(x-2)$ であることを考えると,そもそも「$(x^2-4)(x^2-2x)$」で通分するのが下手な方法であることが分かるはずである。これが所謂「先を読む」ということだと思う。
通分することを考えるが,分母を見て「$(x^2-4)(x^2-2x)$」で通分すると「答えの形」と一致しないと思って諦める人がいるが,諦めずに手を動かしてほしい。
$x^2-2x$ は $x(x-2)$ と因数分解できるのだから,計算した結果「$x-2$ が約分で消えるのかなぁ」と思えれば,白紙にはならないだろう。また,$x^2-4=(x+2)(x-2)$ であることを考えると,そもそも「$(x^2-4)(x^2-2x)$」で通分するのが下手な方法であることが分かるはずである。これが所謂「先を読む」ということだと思う。
\begin{align*}
(与式)&=\dfrac{1}{(x+2)(x-2)}-\dfrac{1}{x(x-2)} \\[4pt]
&=\dfrac{x-(x+2)}{x(x+2)(x-2)} \\[4pt]
&=\dfrac{-2}{x(x^2-4)}
\end{align*}
(与式)&=\dfrac{1}{(x+2)(x-2)}-\dfrac{1}{x(x-2)} \\[4pt]
&=\dfrac{x-(x+2)}{x(x+2)(x-2)} \\[4pt]
&=\dfrac{-2}{x(x^2-4)}
\end{align*}
分数式の加法と減法に関する入試問題
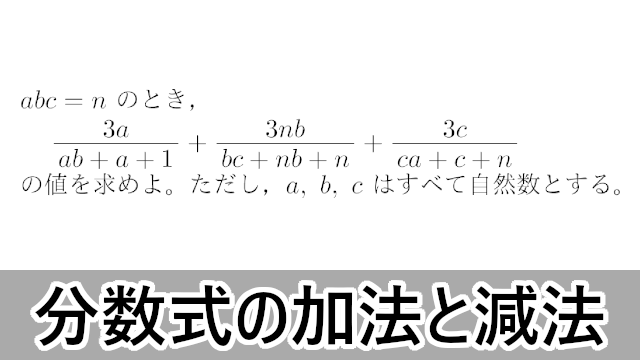
2007年 自治医科大$abc=n$ のとき,
\begin{align*}
\dfrac{3a}{ab+a+1}+\dfrac{3nb}{bc+nb+n}+\dfrac{3c}{ca+c+n}
\end{align*}
の値を求めよ。ただし,$a,~b,~c$ はすべて自然数とする。\dfrac{3a}{ab+a+1}+\dfrac{3nb}{bc+nb+n}+\dfrac{3c}{ca+c+n}
\end{align*}
【考え方と解答】
通分しようとして,分母を「$(ab+a+1)(bc+nb+n)(ca+c+n)$」としてしまうと大変なことになる。複数の式をかけて通分するのではなく,$abc=n$ であることを利用して,それぞれの分数を同じ形にできないかどうかを考えよう。
3つの項のどれから考えるかは人それぞれであるが,最初の項には $n$ がなく,真ん中の項には分母と分子の両方に $n$ があり,最後の項には分母だけに $n$ があることが分かる。
例えば,最後の項の $n$ を $abc$ に変えてみると
通分しようとして,分母を「$(ab+a+1)(bc+nb+n)(ca+c+n)$」としてしまうと大変なことになる。複数の式をかけて通分するのではなく,$abc=n$ であることを利用して,それぞれの分数を同じ形にできないかどうかを考えよう。
3つの項のどれから考えるかは人それぞれであるが,最初の項には $n$ がなく,真ん中の項には分母と分子の両方に $n$ があり,最後の項には分母だけに $n$ があることが分かる。
例えば,最後の項の $n$ を $abc$ に変えてみると
\begin{align*}
\dfrac{3c}{ca+c+n}&=\dfrac{3c}{ca+c+abc} \\[4pt]
&=\dfrac{3}{a+1+ab}
\end{align*}
となり,最初の項と分母が一致する。このように「とりあえずやってみる」ことが重要である。この結果,真ん中の項の分母も $ab+a+1$ に変形することを考える。\dfrac{3c}{ca+c+n}&=\dfrac{3c}{ca+c+abc} \\[4pt]
&=\dfrac{3}{a+1+ab}
\end{align*}
\begin{align*}
\dfrac{3nb}{bc+nb+n}&=\dfrac{3nb}{bc+nb+abc} \\[4pt]
&=\dfrac{3n}{c+n+ac}=\dfrac{3abc}{c+abc+ac} \\[4pt]
&=\dfrac{3ab}{1+ab+a}
\end{align*}
したがって\dfrac{3nb}{bc+nb+n}&=\dfrac{3nb}{bc+nb+abc} \\[4pt]
&=\dfrac{3n}{c+n+ac}=\dfrac{3abc}{c+abc+ac} \\[4pt]
&=\dfrac{3ab}{1+ab+a}
\end{align*}
\begin{align*}
(与式)&=\dfrac{3a}{ab+a+1}+\dfrac{3ab}{1+ab+a}+\dfrac{3}{a+1+ab} \\[4pt]
&=\dfrac{3(ab+a+1)}{ab+a+1}=3
\end{align*}
(与式)&=\dfrac{3a}{ab+a+1}+\dfrac{3ab}{1+ab+a}+\dfrac{3}{a+1+ab} \\[4pt]
&=\dfrac{3(ab+a+1)}{ab+a+1}=3
\end{align*}

ヒロ
変形に手間がかかりすぎているような気がするから,別の方法も考えてみる。
【別解】
\begin{align*}
(与式)&=\dfrac{3ac}{abc+ac+c}+\dfrac{3nb}{bc+nb+abc}+\dfrac{3c}{ca+c+n} \\[4pt]
&=\dfrac{3ac}{n+ac+c}+\dfrac{3n}{c+n+ac}+\dfrac{3c}{ca+c+n} \\[4pt]
&=\dfrac{3(ac+n+c)}{ac+n+c}=3
\end{align*}
(与式)&=\dfrac{3ac}{abc+ac+c}+\dfrac{3nb}{bc+nb+abc}+\dfrac{3c}{ca+c+n} \\[4pt]
&=\dfrac{3ac}{n+ac+c}+\dfrac{3n}{c+n+ac}+\dfrac{3c}{ca+c+n} \\[4pt]
&=\dfrac{3(ac+n+c)}{ac+n+c}=3
\end{align*}

ヒロ
初めから効率の良い解法を追い求めるのではなく,とりあえず解けるようになることを目指すべきである。