Contents
円周上の点における接線の方程式の導出

ヒロ
それでは円周上の点における接線の方程式を導出しよう。

ヒロ
ある直線に垂直な直線の方程式を一般形のまま求められない人は,次の記事を読んでから先に進もう。
原点を中心とする半径 $r$ の円周上の点P$(p,~q)$ における接線 $l$ を考える。
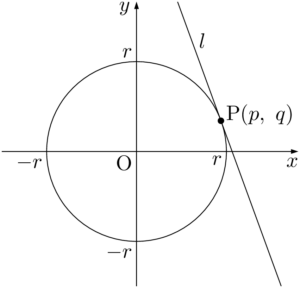
円の接線は,円の中心と接点を結んでできる直線OPと垂直である。
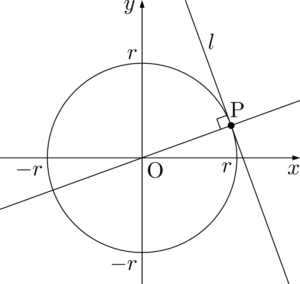
直線OPの方程式は
\begin{align*}
qx-py=0~\cdots\cdots①
\end{align*}
と表せる。基本形の $y=\dfrac{q}{p}x$ だと,点Pが $y$ 軸上の点 $(0,~r)$ や $(0,~-r)$ のときの方程式を表せないから一般形で表している。qx-py=0~\cdots\cdots①
\end{align*}
求める接線 $l$ は点Pを通り直線①に垂直な直線であるから,
\begin{align*}
&p(x-p)+q(y-q)=0 \\[4pt]
&px+qy=p^2+q^2
\end{align*}
となる。ここで,点P$(p,~q)$ は円 $x^2+y^2=r^2$ 上の点であるから&p(x-p)+q(y-q)=0 \\[4pt]
&px+qy=p^2+q^2
\end{align*}
\begin{align*}
p^2+q^2=r^2
\end{align*}
が成り立つ。したがって,点Pにおける接線 $l$ の方程式はp^2+q^2=r^2
\end{align*}
\begin{align*}
px+qy=r^2
\end{align*}
となる。px+qy=r^2
\end{align*}

ヒロ
次は中心が原点でない場合を考えよう。
中心を点C$(a,~b)$ とする半径 $r$ の円を $C$ とし,$C$ 上の点P$(p,~q)$ における接線 $l$ を考える。
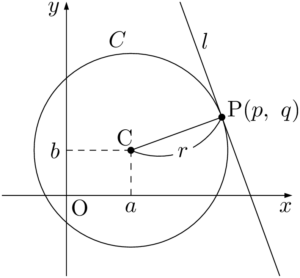
先程と同様に考える。直線CPの方程式は
\begin{align*}
&(q-b)(x-a)-(p-a)(y-b)=0~\cdots\cdots①
\end{align*}
と表せる。ここで,接線 $l$ の方程式を考える上で,$x$ と $y$ の係数だけが重要であり,①の定数項を気にする必要はないため,このまま考える。求める接線 $l$ は,直線①に垂直で点Pを通る直線であるから&(q-b)(x-a)-(p-a)(y-b)=0~\cdots\cdots①
\end{align*}
\begin{align*}
&(p-a)(x-p)+(q-b)(y-q)=0 \\[4pt]
&(p-a)(x-a)+(q-b)(y-b)=(p-a)^2+(q-b)^2
\end{align*}
&(p-a)(x-p)+(q-b)(y-q)=0 \\[4pt]
&(p-a)(x-a)+(q-b)(y-b)=(p-a)^2+(q-b)^2
\end{align*}
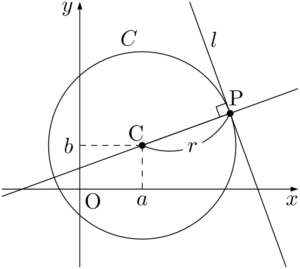
ここで,点P$(p,~q)$ は円 $C$ 上の点であるから
\begin{align*}
(p-a)^2+(q-b)^2=r^2
\end{align*}
が成り立つ。したがって,点Pにおける接線 $l$ の方程式は(p-a)^2+(q-b)^2=r^2
\end{align*}
\begin{align*}
(p-a)(x-a)+(q-b)(y-b)=r^2
\end{align*}
となる。(p-a)(x-a)+(q-b)(y-b)=r^2
\end{align*}



















