ここでは内分点と外分点を表す平面ベクトルについて解説します。
内分点と外分点については,数学2の図形と方程式の単元でも学習します。内分点や外分点のベクトル表記をできるようにすることで,解ける問題が増えます。ベクトルで考える方法も知って使えるようにしましょう。
内分点を表すベクトル

ヒロ
内分点を表すベクトルの公式は次のようになる。
内分点を表すベクトル三角形OABにおいて,$\Vec{OA}=\vec{a}$,$\Vec{OB}=\vec{b}$ とする。線分ABを $m:n$ に内分する点をPとすると,
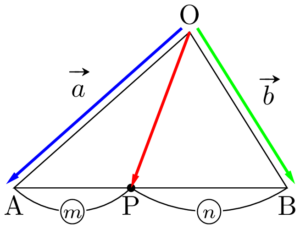
\begin{align*}
\Vec{OP}=\dfrac{n\vec{a}+m\vec{b}}{m+n}
\end{align*}
\Vec{OP}=\dfrac{n\vec{a}+m\vec{b}}{m+n}
\end{align*}

【証明】
\begin{align*}
\Vec{OP}&=\Vec{OA}+\Vec{AP} \\[4pt]
&=\Vec{OA}+\dfrac{m}{m+n}\Vec{AB} \\[4pt]
&=\vec{a}+\dfrac{m}{m+n}(\vec{b}-\vec{a}) \\[4pt]
&=\dfrac{(m+n)\vec{a}+m(\vec{b}-\vec{a})}{m+n} \\[4pt]
&=\dfrac{n\vec{a}+m\vec{b}}{m+n}
\end{align*}
\Vec{OP}&=\Vec{OA}+\Vec{AP} \\[4pt]
&=\Vec{OA}+\dfrac{m}{m+n}\Vec{AB} \\[4pt]
&=\vec{a}+\dfrac{m}{m+n}(\vec{b}-\vec{a}) \\[4pt]
&=\dfrac{(m+n)\vec{a}+m(\vec{b}-\vec{a})}{m+n} \\[4pt]
&=\dfrac{n\vec{a}+m\vec{b}}{m+n}
\end{align*}
外分点を表すベクトル

ヒロ
外分点を表すベクトルの公式は次のようになる。
外分点を表すベクトル三角形OABにおいて,$\Vec{OA}=\vec{a}$,$\Vec{OB}=\vec{b}$ とする。線分ABを $m:n$ に外分する点をPとすると,

\begin{align*}
\Vec{OP}=\dfrac{-n\vec{a}+m\vec{b}}{m-n}
\end{align*}
図は $m>n$ のときの参考図である。\Vec{OP}=\dfrac{-n\vec{a}+m\vec{b}}{m-n}
\end{align*}

【証明】
\begin{align*}
\Vec{OP}&=\Vec{OA}+\Vec{AP} \\[4pt]
&=\Vec{OA}+\dfrac{m}{m-n}\Vec{AB} \\[4pt]
&=\vec{a}+\dfrac{m}{m-n}(\vec{b}-\vec{a}) \\[4pt]
&=\dfrac{(m-n)\vec{a}+m(\vec{b}-\vec{a})}{m-n} \\[4pt]
&=\dfrac{-n\vec{a}+m\vec{b}}{m-n}
\end{align*}
\Vec{OP}&=\Vec{OA}+\Vec{AP} \\[4pt]
&=\Vec{OA}+\dfrac{m}{m-n}\Vec{AB} \\[4pt]
&=\vec{a}+\dfrac{m}{m-n}(\vec{b}-\vec{a}) \\[4pt]
&=\dfrac{(m-n)\vec{a}+m(\vec{b}-\vec{a})}{m-n} \\[4pt]
&=\dfrac{-n\vec{a}+m\vec{b}}{m-n}
\end{align*}

ヒロ
この結果から,「$m:n$ に外分する」は「$m:(-n)$ に内分する」に言い換えられることが分かる。ちなみに「$(-m):n$ に内分する」に言い換えることもできる。
2021年 藤田医科大・ふじた未来入試
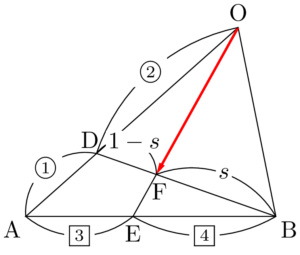
2021年 藤田医科大三角形OABの辺OAを $2:1$ に内分する点をD,辺ABを $3:4$ に内分する点をE,線分BDと線分OEの交点をFとするとき,$\Vec{OF}=\dfrac{\myhako{}}{\myhako{}}\Vec{OA}+\dfrac{\myhako{}}{\myhako{}}\Vec{OB}$ である。
【考え方と解答】
まずは簡単な図を描いて状況を把握しよう。
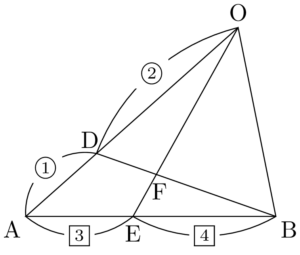
3点O,F,Eが一直線上にあるから,$\Vec{OE}$ の定数倍になることが分かる。また,EはABを $3:4$ に内分するから
ベクトルに拘る必要はなく,メネラウスの定理を利用することで $\textrm{OF}:\textrm{FE}$ を求められることが分かる。
まずは簡単な図を描いて状況を把握しよう。

3点O,F,Eが一直線上にあるから,$\Vec{OE}$ の定数倍になることが分かる。また,EはABを $3:4$ に内分するから
\begin{align*}
\Vec{OE}=\dfrac{4}{7}\Vec{OA}+\dfrac{3}{7}\Vec{OB}
\end{align*}
と表せる。よって,$\textrm{OF}:\textrm{FE}$ を求めることができればこの問題を解くことができる。\Vec{OE}=\dfrac{4}{7}\Vec{OA}+\dfrac{3}{7}\Vec{OB}
\end{align*}
ベクトルに拘る必要はなく,メネラウスの定理を利用することで $\textrm{OF}:\textrm{FE}$ を求められることが分かる。
\begin{align*}
&\dfrac{\textrm{OF}}{\textrm{FE}}\Cdot\dfrac{\textrm{EB}}{\textrm{BA}}\Cdot\dfrac{\textrm{AD}}{\textrm{DO}}=1 \\[4pt]
&\dfrac{\textrm{OF}}{\textrm{FE}}\Cdot\dfrac{4}{7}\Cdot\dfrac{1}{2}=1 \\[4pt]
&\dfrac{\textrm{OF}}{\textrm{FE}}=\dfrac{7}{2}
\end{align*}
よって,$\textrm{OF}:\textrm{FE}=7:2$ となるから&\dfrac{\textrm{OF}}{\textrm{FE}}\Cdot\dfrac{\textrm{EB}}{\textrm{BA}}\Cdot\dfrac{\textrm{AD}}{\textrm{DO}}=1 \\[4pt]
&\dfrac{\textrm{OF}}{\textrm{FE}}\Cdot\dfrac{4}{7}\Cdot\dfrac{1}{2}=1 \\[4pt]
&\dfrac{\textrm{OF}}{\textrm{FE}}=\dfrac{7}{2}
\end{align*}
\begin{align*}
\Vec{OF}&=\dfrac{7}{9}\Vec{OE} \\[4pt]
&=\dfrac{7}{9}\left(\dfrac{4}{7}\Vec{OA}+\dfrac{3}{7}\Vec{OB}\right) \\[4pt]
&=\dfrac{4}{9}\Vec{OA}+\dfrac{1}{3}\Vec{OB}
\end{align*}
\Vec{OF}&=\dfrac{7}{9}\Vec{OE} \\[4pt]
&=\dfrac{7}{9}\left(\dfrac{4}{7}\Vec{OA}+\dfrac{3}{7}\Vec{OB}\right) \\[4pt]
&=\dfrac{4}{9}\Vec{OA}+\dfrac{1}{3}\Vec{OB}
\end{align*}

ヒロ
マーク式試験では,ベクトルを用いた解法に誘導されることもあるから,その解法も知っておこう。
【別の考え方と解答】
点FはOEとBDの交点だから,FがOE上にあることとBD上にあることをベクトルを用いて表すことを考える。条件が2つあるから,文字を2つ使っても方程式を2本立てることができれば解けるはず。
まず,3点O,F,Eが一直線上にあるから,$\Vec{OF}=t\Vec{OE}$ と表せる。
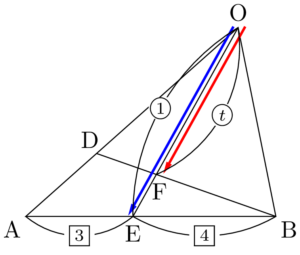
さらに $\textrm{AE}:\textrm{EB}=3:4$ より
$\Vec{OD}=\dfrac{2}{3}\Vec{OA}$ だから
これを④に代入すると
よって,$\Vec{OF}=\dfrac{4}{9}\Vec{OA}+\dfrac{1}{3}\Vec{OB}$
点FはOEとBDの交点だから,FがOE上にあることとBD上にあることをベクトルを用いて表すことを考える。条件が2つあるから,文字を2つ使っても方程式を2本立てることができれば解けるはず。
まず,3点O,F,Eが一直線上にあるから,$\Vec{OF}=t\Vec{OE}$ と表せる。

さらに $\textrm{AE}:\textrm{EB}=3:4$ より
\begin{align*}
\Vec{OE}=\dfrac{4}{7}\Vec{OA}+\dfrac{3}{7}\Vec{OB}
\end{align*}
と表せるから,\Vec{OE}=\dfrac{4}{7}\Vec{OA}+\dfrac{3}{7}\Vec{OB}
\end{align*}
\begin{align*}
\Vec{OF}=\dfrac{4}{7}t\Vec{OA}+\dfrac{3}{7}t\Vec{OB}~\cdots\cdots①
\end{align*}
となる。次に $\textrm{BF}:\textrm{FD}=s:(1-s)$ とおくと,\Vec{OF}=\dfrac{4}{7}t\Vec{OA}+\dfrac{3}{7}t\Vec{OB}~\cdots\cdots①
\end{align*}
\begin{align*}
\Vec{OF}=s\Vec{OD}+(1-s)\Vec{OB}
\end{align*}
と表せる。\Vec{OF}=s\Vec{OD}+(1-s)\Vec{OB}
\end{align*}

$\Vec{OD}=\dfrac{2}{3}\Vec{OA}$ だから
\begin{align*}
\Vec{OF}=\dfrac{2}{3}s\Vec{OA}+(1-s)\Vec{OB}~\cdots\cdots②
\end{align*}
となる。$\Vec{OA}$と$\Vec{OB}$ は平行でなく $\vec{0}$ でないから,①と②から\Vec{OF}=\dfrac{2}{3}s\Vec{OA}+(1-s)\Vec{OB}~\cdots\cdots②
\end{align*}
\begin{align*}
\begin{cases}
\dfrac{4}{7}t=\dfrac{2}{3}s~\cdots\cdots③ \\[4pt]
\dfrac{3}{7}t=1-s~\cdots\cdots④
\end{cases}
\end{align*}
③より,$t=\dfrac{7}{6}s$\begin{cases}
\dfrac{4}{7}t=\dfrac{2}{3}s~\cdots\cdots③ \\[4pt]
\dfrac{3}{7}t=1-s~\cdots\cdots④
\end{cases}
\end{align*}
これを④に代入すると
\begin{align*}
&\dfrac{1}{2}s=1-s \\[4pt]
&s=2-2s \\[4pt]
&s=\dfrac{2}{3}
\end{align*}
このとき,$t=\dfrac{7}{9}$&\dfrac{1}{2}s=1-s \\[4pt]
&s=2-2s \\[4pt]
&s=\dfrac{2}{3}
\end{align*}
よって,$\Vec{OF}=\dfrac{4}{9}\Vec{OA}+\dfrac{1}{3}\Vec{OB}$