これまでに扱ってきた「共有点」には,次のものがあります。
- 直線と直線
- 直線と放物線
- 放物線と放物線
円の方程式を扱うようになったことで,「円と直線」「円と円」「円と放物線」の共有点に関する問題も考えることができます。
今回はその中の1つである「円と直線の共有点」について説明します。
Contents
円とy軸と平行な直線の共有点

ヒロ
平面上の直線は「$y$ 軸と平行な直線」と「$y$ 軸と平行でない直線」の2つに分類される。

ヒロ
まずは,$y$ 軸と平行な直線と円の共有点の座標を求める方法を説明する。
【直線が $y$ 軸と平行であるとき】
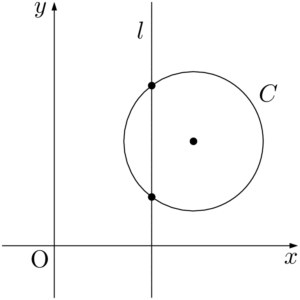
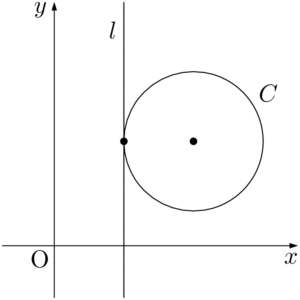
円 $C:x^2+y^2+lx+my+n=0$ と直線 $l:x=a$ の共有点を求める。円 $C$ と直線 $l$ の共有点は,当たり前であるが,円 $C$ 上の点であり,直線 $l$ 上の点でもある。つまり $C,~l$ の両方の方程式をみたす $x,~y$ が共有点の座標である。したがって,連立方程式
\begin{align*}
\begin{cases}
x^2+y^2+lx+my+n=0 &~\cdots\cdots① \\[4pt]
x=a &~\cdots\cdots②
\end{cases}
\end{align*}
の解 $(x,~y)$ が $C,~l$ の共有点の座標である。②を①に代入すると\begin{cases}
x^2+y^2+lx+my+n=0 &~\cdots\cdots① \\[4pt]
x=a &~\cdots\cdots②
\end{cases}
\end{align*}
\begin{align*}
&a^2+y^2+la+my+n=0 \\[4pt]
&y^2+my+a^2+la+n=0~\cdots\cdots③
\end{align*}
③を解くことで,共有点の $y$ 座標が得られる。&a^2+y^2+la+my+n=0 \\[4pt]
&y^2+my+a^2+la+n=0~\cdots\cdots③
\end{align*}
③が異なる2つの実数解をもつとき,共有点は2つあり,$C$ と $l$ は異なる2点で交わる。また,③が重解をもつとき,共有点は1つで,$C$ と $l$ は接する。