2020年センター試験 数学ⅡB 第1問 指数関数・対数関数の解説をします。
まだ問題を解いていない人は解いてから解説を読んでください。
2020年 センターⅡB 第1問 指数・対数関数(1) $t$ は正の実数であり,$t^{\frac{1}{3}}-t^{-\frac{1}{3}}=-3$ を満たすとする。 このとき
(2) $x,~y$ は正の実数とする。連立不等式
$X=\log_3x,~Y=\log_3y$ とおくと,②は
$X,~Y$ が④と⑤を満たすとき,$Y$ のとり得る最大の整数の値は $\myBox{ヘ}$ である。 また,$x,~y$ が②,③と $\log_3y=\mybox{ヘ}$ を同時に満たすとき, $x$ のとり得る最大の整数の値は $\myBox{ホ}$ である。
\begin{align*} t^{\frac{2}{3}}-t^{-\frac{2}{3}}=\myBox{タチ} \end{align*}
である。さらに \begin{align*} t^{\frac{1}{3}}+t^{-\frac{1}{3}}=\sqrt{\myBox{ツテ}},~t-t^{-1}=\myBox{トナニ} \end{align*}
である。(2) $x,~y$ は正の実数とする。連立不等式
\begin{align*} \begin{cases} \log_3(x\sqrt{y})\leqq5 &~\cdots\cdots② \\[4pt] \log_{81}\dfrac{y}{x^3}\leqq1 &~\cdots\cdots③ \end{cases} \end{align*}
について考える。$X=\log_3x,~Y=\log_3y$ とおくと,②は
\begin{align*} \myBox{ヌ}\,X+Y\leqq\myBox{ネノ}~\cdots\cdots④ \end{align*}
と変形でき,③は \begin{align*} \myBox{ハ}\,X-Y\geqq\myBox{ヒフ}~\cdots\cdots⑤ \end{align*}
と変形できる。$X,~Y$ が④と⑤を満たすとき,$Y$ のとり得る最大の整数の値は $\myBox{ヘ}$ である。 また,$x,~y$ が②,③と $\log_3y=\mybox{ヘ}$ を同時に満たすとき, $x$ のとり得る最大の整数の値は $\myBox{ホ}$ である。
(1)の考え方と解答

ヒロ
対称式の変形の応用問題だね。
【タチの解答】
$t^{\frac{1}{3}}=a$ とおくと,$a-\dfrac{1}{a}=-3$ であるから
$t^{\frac{1}{3}}=a$ とおくと,$a-\dfrac{1}{a}=-3$ であるから
\begin{align*} t^{\frac{2}{3}}+t^{-\frac{2}{3}} &=a^2+\dfrac{1}{a^2} \\[4pt] &=\left(a-\dfrac{1}{a}\right)^2+2 \\[4pt] &=(-3)^2+2 \\[4pt] &=11 \end{align*}

ヒロ
同じように進めていこう。
【ツ~ニの解答】
\begin{align*} \left(t^{\frac{1}{3}}+t^{-\frac{1}{3}}\right)^2 &=\left(a+\dfrac{1}{a}\right)^2 \\[4pt] &=\left(a-\dfrac{1}{a}\right)^2+4 \\[4pt] &=(-3)^2+4 \\[4pt] &=13 \end{align*}
$t^{\frac{1}{3}}+t^{-\frac{1}{3}}>0$ より, \begin{align*} t^{\frac{1}{3}}+t^{-\frac{1}{3}}=\sqrt{13} \end{align*}
また \begin{align*} t-t^{-1} &=a^3-\dfrac{1}{a^3} \\[4pt] &=\left(a-\dfrac{1}{a}\right)^3+3\left(a-\dfrac{1}{a}\right) \\[4pt] &=(-3)^3+3\Cdota(-3) \\[4pt] &=-36 \end{align*}
(2)の考え方と解答
(2) $x,~y$ は正の実数とする。連立不等式
\begin{align*} \begin{cases} \log_3(x\sqrt{y})\leqq5 &~\cdots\cdots② \\[4pt] \log_{81}\dfrac{y}{x^3}\leqq1 &~\cdots\cdots③ \end{cases} \end{align*}について考える。
$X=\log_3x,~Y=\log_3y$ とおくと,②は\begin{align*} \myBox{ヌ}\,X+Y\leqq\myBox{ネノ}~\cdots\cdots④ \end{align*}と変形でき,③は\begin{align*} \myBox{ハ}\,X-Y\geqq\myBox{ヒフ}~\cdots\cdots⑤ \end{align*}と変形できる。
$X,~Y$ が④と⑤を満たすとき,$Y$ のとり得る最大の整数の値は $\myBox{ヘ}$ である。 また,$x,~y$ が②,③と $\log_3y=\mybox{ヘ}$ を同時に満たすとき, $x$ のとり得る最大の整数の値は $\myBox{ホ}$ である。

ヒロ
1つずつ変形しよう。
【ヌ~フの解答】
②より
②より
\begin{align*} &\log_3x+\dfrac{1}{2}\log_3y\leqq5 \\[4pt] &X+\dfrac{1}{2}Y\leqq5 \\[4pt] &2X+Y\leqq10 \end{align*}
③より \begin{align*} &\log_{81}y-\log_{81}x^3\leqq1 \\[4pt] &\log_3y^{\frac{1}{4}}-\log_3x^{\frac{3}{4}}\leqq1 \\[4pt] &\log_3y-3\log_3x\leqq4 \\[4pt] &3X-Y\geqq-4 \end{align*}

ヒロ
上の変形では次の公式を利用している。
対数法則$\log_ab=\log_{a^n}b^n$ が成り立つから
\begin{align*} \log_{81}y&=\log_{81^{\frac{1}{4}}}y^{\frac{1}{4}} \\[4pt] &=\log_3y^{\frac{1}{4}} \end{align*}

ヒロ
④と⑤が表す領域を図示して考えよう。
【ヘの解答】
④と⑤をともに満たすような点 $(X,~Y)$ の存在範囲は下図の斜線部分である。 ただし境界を含む。
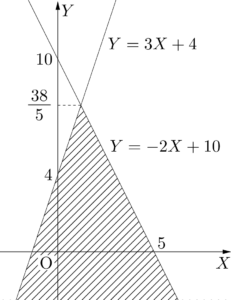
上図より,$Y\leqq\dfrac{38}{5}$ であるから,$Y$ のとり得る最大の整数の値は7である。
④と⑤をともに満たすような点 $(X,~Y)$ の存在範囲は下図の斜線部分である。 ただし境界を含む。

上図より,$Y\leqq\dfrac{38}{5}$ であるから,$Y$ のとり得る最大の整数の値は7である。

ヒロ
最後の $x$ の最大の整数値を求めよう。
【ホの解答】
$\log_3y=7$ のとき $Y=7$ だから,$Y=-2X+10$ に代入すると
$\log_3y=7$ のとき $Y=7$ だから,$Y=-2X+10$ に代入すると
\begin{align*} &7=-2X+10 \\[4pt] &X=\dfrac{3}{2} \end{align*}
である。グラフより $X\leqq\dfrac{3}{2}$ であるから \begin{align*} &\log_3x\leqq\dfrac{3}{2} \\[4pt] &x\leqq3^{\frac{3}{2}}=\sqrt{27} \end{align*}
よって,$x$ のとり得る最大の整数の値は5である。2020年 センター数学ⅡB 指数関数・対数関数を解いた感想

ヒロ
指数が分数になっているものは文字で置き換えることで,小さい数字を書かなくて済むため, 書きやすくなり短時間で解くことができる。

ヒロ
また考えやすくなるメリットもあるため,文字の置き換えはオススメ。

ヒロ
(2)の取り得る値の範囲については,領域を図示して考えて確実に得点したい。




















