2018年センター試験 数学ⅡB 第1問三角関数の解説をします。
まだ問題を解いていない人は解いてから解説を読んでください。
2018年 センターⅡB 三角関数(1) 1ラジアンとは,$\myBox{ア}$ のことである。$\myBox{ア}$ に当てはまるものを,次の⓪~③のうちから一つ選べ。
⓪ 半径が1,面積が1の扇形の中心角の大きさ
⓪ 半径が $\pi$,面積が1の扇形の中心角の大きさ
⓪ 半径が1,弧の長さが1の扇形の中心角の大きさ
⓪ 半径が $\pi$,弧の長さが1の扇形の中心角の大きさ
(2) 144$\Deg$ を弧度で表すと $\dfrac{\myBox{イ}}{\myBox{ウ}}~\pi$ ラジアンである。また,$\dfrac{23}{12}\pi$ ラジアンを度で表すと $\myBox{エオカ}\Deg$ である。
(3) $\dfrac{\pi}{2}\leqq\theta\leqq\pi$ の範囲で
$x=\theta+\dfrac{\pi}{5}$ とおくと,①は
⓪ 半径が1,面積が1の扇形の中心角の大きさ
⓪ 半径が $\pi$,面積が1の扇形の中心角の大きさ
⓪ 半径が1,弧の長さが1の扇形の中心角の大きさ
⓪ 半径が $\pi$,弧の長さが1の扇形の中心角の大きさ
(2) 144$\Deg$ を弧度で表すと $\dfrac{\myBox{イ}}{\myBox{ウ}}~\pi$ ラジアンである。また,$\dfrac{23}{12}\pi$ ラジアンを度で表すと $\myBox{エオカ}\Deg$ である。
(3) $\dfrac{\pi}{2}\leqq\theta\leqq\pi$ の範囲で
\begin{align*}
2\sin\left(\theta+\dfrac{\pi}{5}\right)-2\cos\left(\theta+\dfrac{\pi}{30}\right)=1 \cdots\cdots①
\end{align*}
を満たす $\theta$ の値を求めよう。2\sin\left(\theta+\dfrac{\pi}{5}\right)-2\cos\left(\theta+\dfrac{\pi}{30}\right)=1 \cdots\cdots①
\end{align*}
$x=\theta+\dfrac{\pi}{5}$ とおくと,①は
\begin{align*}
2\sin x-2\cos\left(x-\dfrac{\pi}{\myBox{キ}}\right)=1
\end{align*}
と表せる。加法定理を用いると,この式は2\sin x-2\cos\left(x-\dfrac{\pi}{\myBox{キ}}\right)=1
\end{align*}
\begin{align*}
\sin x-\sqrt{\myBox{ク}}\cos x=1
\end{align*}
となる。さらに,三角関数の合成を用いると\sin x-\sqrt{\myBox{ク}}\cos x=1
\end{align*}
\begin{align*}
\sin\left(x-\dfrac{\pi}{\myBox{ケ}}\right)=\dfrac{1}{\myBox{コ}}
\end{align*}
と変形できる。$x=\theta+\dfrac{\pi}{5},~\dfrac{\pi}{2}\leqq\theta\leqq\pi$ だから,$\theta=\dfrac{\myBox{サシ}}{\myBox{スセ}}~\pi$ である。\sin\left(x-\dfrac{\pi}{\myBox{ケ}}\right)=\dfrac{1}{\myBox{コ}}
\end{align*}
(1)の解答

ヒロ
最初は弧度法の単位のラジアンの理解を問う問題だね。
【アの解答】
1ラジアンとは,半径が1,弧の長さが1の扇形の中心角の大きさであるから,$\myBox{ア}=②$
1ラジアンとは,半径が1,弧の長さが1の扇形の中心角の大きさであるから,$\myBox{ア}=②$
(2)の解答

ヒロ
次は度数法と弧度法の変換の問題。180$\Deg$ が $\pi$ ラジアンであることを利用しよう。
【イ~カの解答】
\begin{align*}
&144\times\dfrac{\pi}{180}=\dfrac{4}{5}\pi \\[4pt]
&\dfrac{23}{12}\pi\times\dfrac{180}{\pi}=345\Deg
\end{align*}
&144\times\dfrac{\pi}{180}=\dfrac{4}{5}\pi \\[4pt]
&\dfrac{23}{12}\pi\times\dfrac{180}{\pi}=345\Deg
\end{align*}
(3)の解答

ヒロ
誘導に乗って,①を $x$ の方程式に書き直そう。
【キの解答】
$x=\theta+\dfrac{\pi}{5}$ とおくと,
$x=\theta+\dfrac{\pi}{5}$ とおくと,
\begin{align*}
\theta+\dfrac{\pi}{30}&=x-\dfrac{\pi}{5}+\dfrac{\pi}{30} \\[4pt]
&=\theta-\dfrac{\pi}{6}
\end{align*}
となるから,①は\theta+\dfrac{\pi}{30}&=x-\dfrac{\pi}{5}+\dfrac{\pi}{30} \\[4pt]
&=\theta-\dfrac{\pi}{6}
\end{align*}
\begin{align*}
&2\sin x-2\cos\left(x-\dfrac{\pi}{6}\right)=1
\end{align*}
と表せる。&2\sin x-2\cos\left(x-\dfrac{\pi}{6}\right)=1
\end{align*}

ヒロ
ここから加法定理を用いて変形していこう。
【クの解答】
\begin{align*}
&2\sin x-2\cos\left(x-\dfrac{\pi}{6}\right)=1 \\[4pt]
&2\sin x-2\left(\cos x\cos\dfrac{\pi}{6}+\sin x\sin\dfrac{\pi}{6}\right)=1 \\[4pt]
&2\sin x-(\sqrt{3}\cos x+\sin x)=1 \\[4pt]
&\sin x-\sqrt{3}\cos x=1
\end{align*}
&2\sin x-2\cos\left(x-\dfrac{\pi}{6}\right)=1 \\[4pt]
&2\sin x-2\left(\cos x\cos\dfrac{\pi}{6}+\sin x\sin\dfrac{\pi}{6}\right)=1 \\[4pt]
&2\sin x-(\sqrt{3}\cos x+\sin x)=1 \\[4pt]
&\sin x-\sqrt{3}\cos x=1
\end{align*}

ヒロ
次は三角関数の合成を用いて角をまとめよう。
【ケコの解答】
\begin{align*}
&\sin x-\sqrt{3}\cos x=1 \\[4pt]
&2\left(\sin x\Cdota\dfrac{1}{2}-\cos x\Cdota\dfrac{\sqrt{3}}{2}\right)=1 \\[4pt]
&2\sin\left(x-\dfrac{\pi}{3}\right)=1 \\[4pt]
&\sin\left(x-\dfrac{\pi}{3}\right)=\dfrac{1}{2}
\end{align*}
&\sin x-\sqrt{3}\cos x=1 \\[4pt]
&2\left(\sin x\Cdota\dfrac{1}{2}-\cos x\Cdota\dfrac{\sqrt{3}}{2}\right)=1 \\[4pt]
&2\sin\left(x-\dfrac{\pi}{3}\right)=1 \\[4pt]
&\sin\left(x-\dfrac{\pi}{3}\right)=\dfrac{1}{2}
\end{align*}

ヒロ
最後は条件を満たす $\theta$ の値を求めよう。
【サ~セの解答】
$x=\theta+\dfrac{\pi}{5}$ より
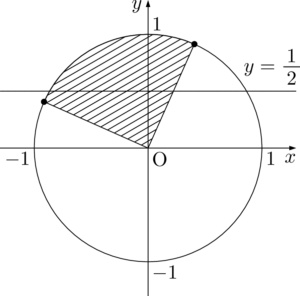
よって,$\sin\left(x-\dfrac{\pi}{3}\right)=\dfrac{1}{2}$ より
$x=\theta+\dfrac{\pi}{5}$ より
\begin{align*}
x-\dfrac{\pi}{3}&=\theta+\dfrac{\pi}{5}-\dfrac{\pi}{3} \\[4pt]
&=\theta-\dfrac{2}{15}\pi
\end{align*}
であるから,$\dfrac{\pi}{2}\leqq\theta\leqq\pi$ のときx-\dfrac{\pi}{3}&=\theta+\dfrac{\pi}{5}-\dfrac{\pi}{3} \\[4pt]
&=\theta-\dfrac{2}{15}\pi
\end{align*}
\begin{align*}
&\dfrac{\pi}{2}-\dfrac{2}{15}\pi\leqq x-\dfrac{\pi}{3}\leqq\pi-\dfrac{2}{15}\pi
\end{align*}
&\dfrac{\pi}{2}-\dfrac{2}{15}\pi\leqq x-\dfrac{\pi}{3}\leqq\pi-\dfrac{2}{15}\pi
\end{align*}

よって,$\sin\left(x-\dfrac{\pi}{3}\right)=\dfrac{1}{2}$ より
\begin{align*}
&x-\dfrac{\pi}{3}=\dfrac{5}{6}\pi \\[4pt]
&\theta-\dfrac{2}{15}\pi=\dfrac{5}{6}\pi \\[4pt]
&\theta=\dfrac{25+4}{30}\pi=\dfrac{29}{30}\pi
\end{align*}
&x-\dfrac{\pi}{3}=\dfrac{5}{6}\pi \\[4pt]
&\theta-\dfrac{2}{15}\pi=\dfrac{5}{6}\pi \\[4pt]
&\theta=\dfrac{25+4}{30}\pi=\dfrac{29}{30}\pi
\end{align*}

ヒロ
上の解説では,単位円を正確に描いているが,実際にはそれなりで大丈夫だよ。

ヒロ
今回の場合は,$\dfrac{\pi}{6}$ と $\dfrac{5}{6}\pi$ のどちらが解であるかが分かる程度に描こう。描かずに頭の中で処理できるなら,もちろんそれでも構わない。
2018年 センター数学ⅡB 三角関数を解いた感想

ヒロ
それほど多くはないと思うが,「ラジアンの定義って何だったっけ?」となる人は最初で躓くことになるので,パニックになった人もいるかもしれない。

ヒロ
1999年の東大で $\sin\theta$ や $\cos\theta$ の定義を述べる問題が出題されたように,定義についてもしっかり理解しておこう。

ヒロ
逆に数学が得意な人からすれば,(1),(2)は簡単すぎる問題で,こんな問題では差が付かないから困るという感情を持ったのではないだろうか。

ヒロ
(3)は計算が少しややこしくなるように作られているが,よくある問題なので,(1),(2)を簡単に感じた人にとっては,何も苦労しなかっただろう。




















