2020年センター試験 数学ⅠA 第1問 平面図形の解説をします。
まだ問題を解いていない人は解いてから解説を読んでください。
2020年 センターⅠA 第1問 平面図形$\sankaku{ABC}$ において,辺BCを $7:1$ に内分する点をDとし,
辺ACを $7:1$ に内分する点をEとする。線分ADと線分BEの交点をFとし,
直線CFと辺ABの交点をGとすると
4点B,D,F,Gが同一円周上にあり,かつ $\mathrm{FD}=1$ のとき
⓪ $\kaku{BGE}$ ① $\kaku{ADB}$ ② $\kaku{ABC}$ ③ $\kaku{BAD}$
辺ACを $7:1$ に内分する点をEとする。線分ADと線分BEの交点をFとし,
直線CFと辺ABの交点をGとすると
\begin{align*}
\dfrac{\mathrm{GB}}{\mathrm{AG}}=\myBox{ア},~
\dfrac{\mathrm{FD}}{\mathrm{AF}}=\dfrac{\myBox{イ}}{\myBox{ウ}},~
\dfrac{\mathrm{FC}}{\mathrm{GF}}=\dfrac{\myBox{エ}}{\myBox{オ}}
\end{align*}
である。したがって\dfrac{\mathrm{GB}}{\mathrm{AG}}=\myBox{ア},~
\dfrac{\mathrm{FD}}{\mathrm{AF}}=\dfrac{\myBox{イ}}{\myBox{ウ}},~
\dfrac{\mathrm{FC}}{\mathrm{GF}}=\dfrac{\myBox{エ}}{\myBox{オ}}
\end{align*}
\begin{align*}
\dfrac{\sankaku{CDG}の面積}{\sankaku{BFG}の面積}=\dfrac{\myBox{カ}}{\myBox{キク}}
\end{align*}
\dfrac{\sankaku{CDG}の面積}{\sankaku{BFG}の面積}=\dfrac{\myBox{カ}}{\myBox{キク}}
\end{align*}
4点B,D,F,Gが同一円周上にあり,かつ $\mathrm{FD}=1$ のとき
\begin{align*}
\mathrm{AB}=\myBox{ケコ}
\end{align*}
である。さらに,$\mathrm{AE}=3\sqrt{7}$ とするとき, $\mathrm{AE}\Cdot\mathrm{AC}=\myBox{サシ}$ であり\mathrm{AB}=\myBox{ケコ}
\end{align*}
\begin{align*}
\kaku{AEG}=\myBox{ス}
\end{align*}
である。$\mybox{ス}$ に当てはまるものを,次の⓪~③のうちから一つ選べ。\kaku{AEG}=\myBox{ス}
\end{align*}
⓪ $\kaku{BGE}$ ① $\kaku{ADB}$ ② $\kaku{ABC}$ ③ $\kaku{BAD}$
考え方と解答

ヒロ
まずは適当な図を描いて状況を把握しよう。
【状況把握するための図】
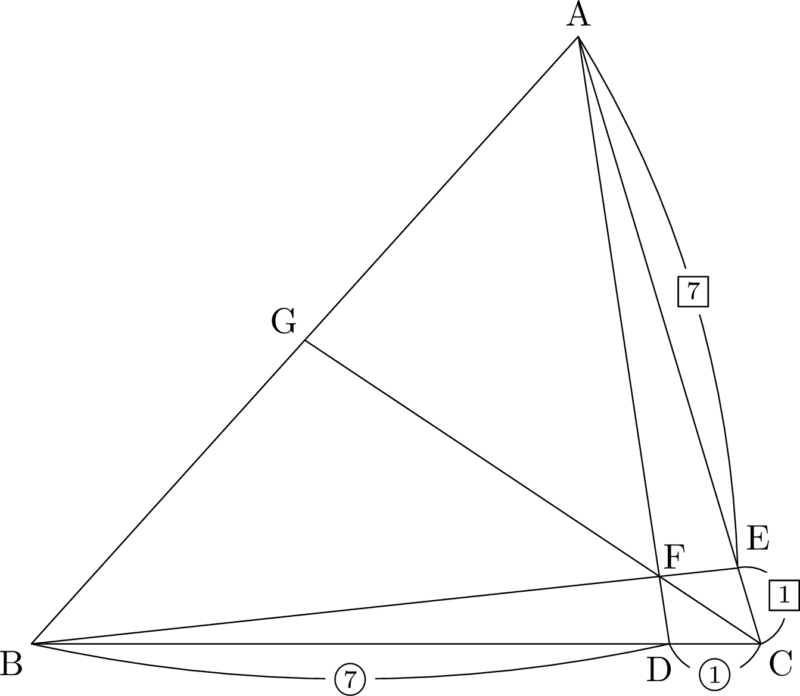

ヒロ
通常ならチェバの定理・メネラウスの定理を活用するところだけど,面倒なので速答法で処理しよう。
三角形と辺の比$\sankaku{ABC} $において,$\mathrm{AR:RB}=a:b$, $\mathrm{AQ:QC}=c:d$ であるとする。
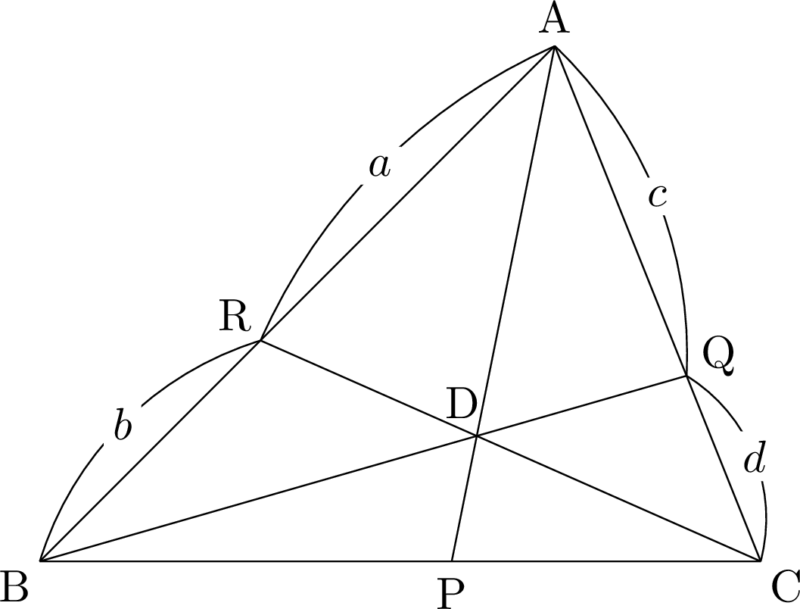
次の図のように,BRとCQが同じ値になるように比を直すと,同じ色の部分は同じ数字になる。
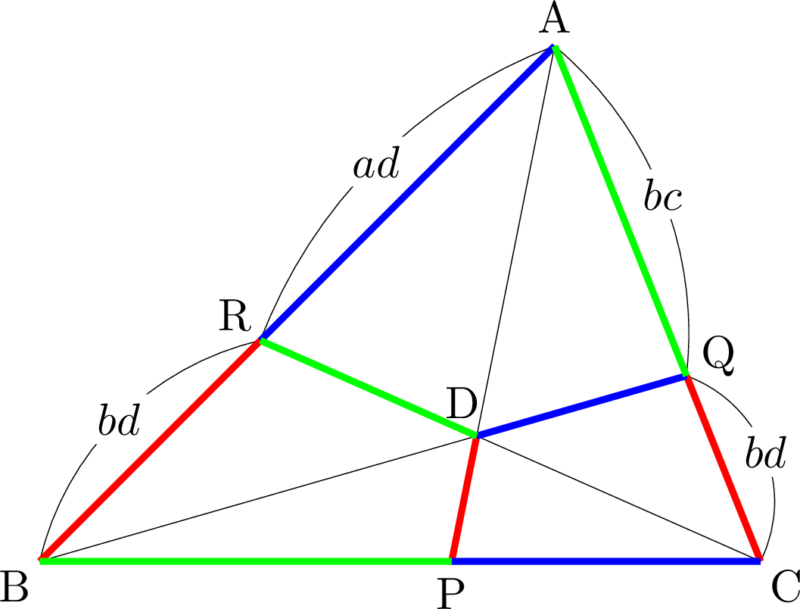
また,

次の図のように,BRとCQが同じ値になるように比を直すと,同じ色の部分は同じ数字になる。

また,
\begin{align*}
\mathrm{AD:DP}=(ad+bc):bd
\end{align*}
が成り立つ。$\mathrm{BD:DQ}$, $\mathrm{CD:DR}$ も同様に求めることができる。\mathrm{AD:DP}=(ad+bc):bd
\end{align*}
【ア~オの解答】
分かりやすく色を付けて,数字を書くと次のようになる。
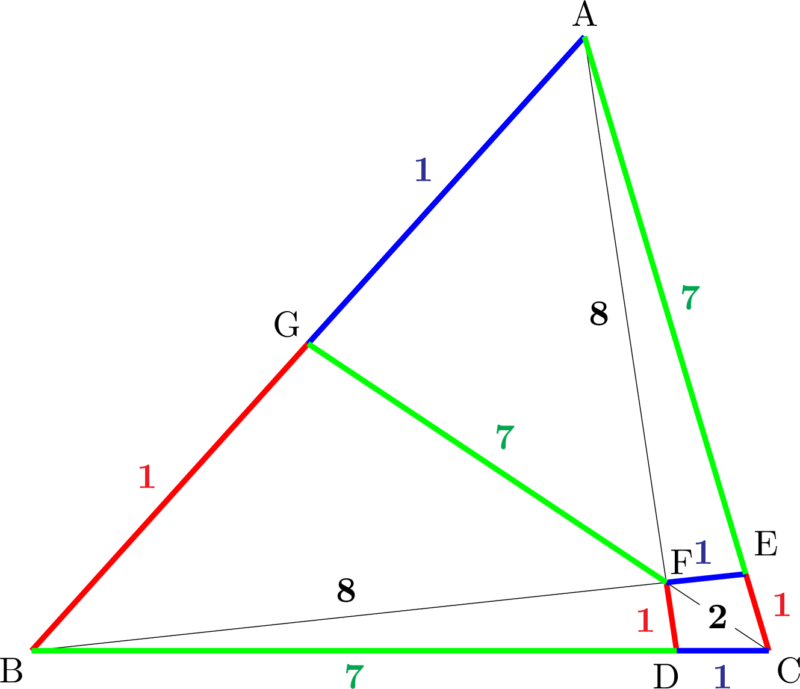
これより
分かりやすく色を付けて,数字を書くと次のようになる。

これより
\begin{align*}
&\dfrac{\mathrm{GB}}{\mathrm{AG}}=1,~\dfrac{\mathrm{FD}}{\mathrm{AF}}=\dfrac{1}{8},~\dfrac{\mathrm{FC}}{\mathrm{GF}}=\dfrac{2}{7}
\end{align*}
&\dfrac{\mathrm{GB}}{\mathrm{AG}}=1,~\dfrac{\mathrm{FD}}{\mathrm{AF}}=\dfrac{1}{8},~\dfrac{\mathrm{FC}}{\mathrm{GF}}=\dfrac{2}{7}
\end{align*}

ヒロ
次は三角形の面積比を求める問題。
【カ~クの解答】
$\sankaku{CDG}$ は下図の斜線部分である。
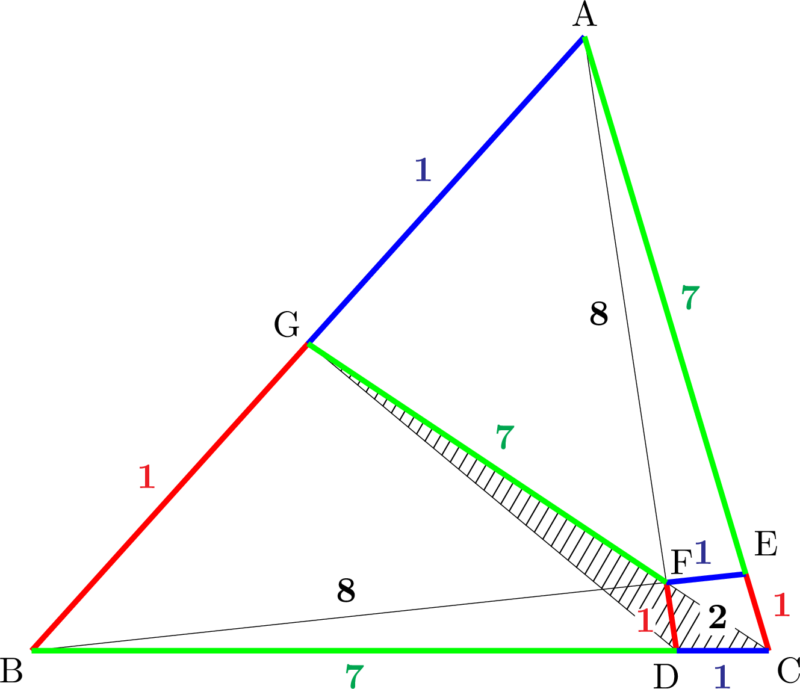
$\sankaku{ABC}$ の面積を $S$ とすると
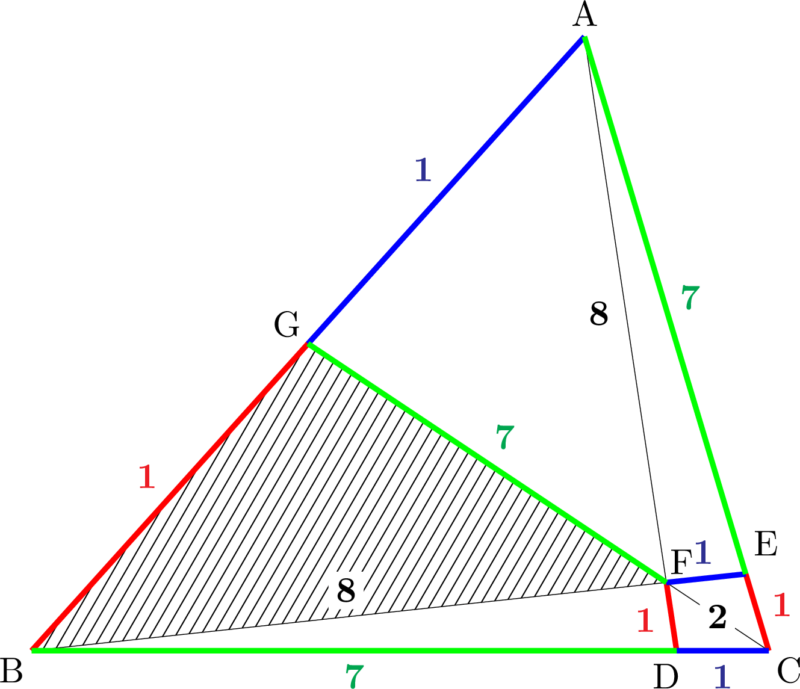
$\sankaku{BFG}$ の面積を $S$ で表すと次のようになる。
$\sankaku{CDG}$ は下図の斜線部分である。

$\sankaku{ABC}$ の面積を $S$ とすると
\begin{align*}
\sankaku{CDG}&=\dfrac{1}{8}\sankaku{CBG} \\[4pt]
&=\dfrac{1}{8}\Cdota\dfrac{1}{2}\sankaku{ABC} \\[4pt]
&=\dfrac{1}{16}S
\end{align*}
また,$\sankaku{BFG}$ は下図の斜線部分である。\sankaku{CDG}&=\dfrac{1}{8}\sankaku{CBG} \\[4pt]
&=\dfrac{1}{8}\Cdota\dfrac{1}{2}\sankaku{ABC} \\[4pt]
&=\dfrac{1}{16}S
\end{align*}

$\sankaku{BFG}$ の面積を $S$ で表すと次のようになる。
\begin{align*}
\sankaku{BFG}&=\dfrac{7}{9}\sankaku{BCG} \\[4pt]
&=\dfrac{7}{9}\Cdota\dfrac{1}{2}\sankaku{ABC} \\[4pt]
&=\dfrac{7}{18}S
\end{align*}
よって\sankaku{BFG}&=\dfrac{7}{9}\sankaku{BCG} \\[4pt]
&=\dfrac{7}{9}\Cdota\dfrac{1}{2}\sankaku{ABC} \\[4pt]
&=\dfrac{7}{18}S
\end{align*}
\begin{align*}
\dfrac{\sankaku{CDG}の面積}{\sankaku{BFG}の面積}
&=\dfrac{\dfrac{1}{16}S}{\dfrac{7}{18}S} \\[4pt]
&=\dfrac{1}{16}\Cdota\dfrac{18}{7} \\[4pt]
&=\dfrac{9}{56}
\end{align*}
\dfrac{\sankaku{CDG}の面積}{\sankaku{BFG}の面積}
&=\dfrac{\dfrac{1}{16}S}{\dfrac{7}{18}S} \\[4pt]
&=\dfrac{1}{16}\Cdota\dfrac{18}{7} \\[4pt]
&=\dfrac{9}{56}
\end{align*}

ヒロ
ABの長さを求めるために,円を描いて考えよう。

ヒロ
既に描いている図に円を追加して描くため,多少汚くなるが,頑張って描こう。
【ケコの解答】
4点B,D,F,Gが同一円周上にあるとき,その円を描くと次の図のようになる。
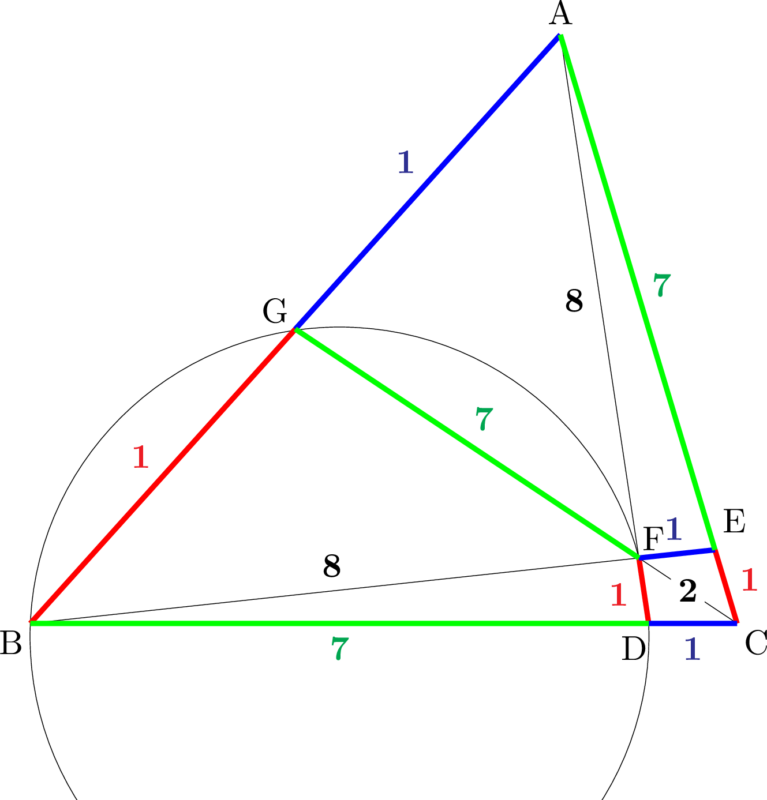
$\mathrm{FD}=1$ のとき,$\mathrm{AF}=8$ であり,$\mathrm{AB}=x$ とおくと,$\mathrm{AG}=\dfrac{1}{2}x$ である。方べきの定理より
4点B,D,F,Gが同一円周上にあるとき,その円を描くと次の図のようになる。

$\mathrm{FD}=1$ のとき,$\mathrm{AF}=8$ であり,$\mathrm{AB}=x$ とおくと,$\mathrm{AG}=\dfrac{1}{2}x$ である。方べきの定理より
\begin{align*}
&\mathrm{AF}\Cdota\mathrm{AD}=\mathrm{AG}\Cdota\mathrm{AB} \\[4pt]
&8\Cdota9=\dfrac{1}{2}x\Cdota x \\[4pt]
&x^2=16\Cdota9
\end{align*}
&\mathrm{AF}\Cdota\mathrm{AD}=\mathrm{AG}\Cdota\mathrm{AB} \\[4pt]
&8\Cdota9=\dfrac{1}{2}x\Cdota x \\[4pt]
&x^2=16\Cdota9
\end{align*}

ヒロ
次のAEとACの辺の長さの積を求めよう。
【サシの解答】
$\mathrm{AC}=\dfrac{8}{7}\mathrm{AE}$ より,$\mathrm{AE}=3\sqrt{7}$ のとき,
$\mathrm{AC}=\dfrac{8}{7}\mathrm{AE}$ より,$\mathrm{AE}=3\sqrt{7}$ のとき,
\begin{align*}
\mathrm{AE}\Cdota\mathrm{AC}&=\dfrac{8}{7}\mathrm{AE}^2 \\[4pt]
&=\dfrac{8}{7}(3\sqrt{7})^2 \\[4pt]
&=72
\end{align*}
\mathrm{AE}\Cdota\mathrm{AC}&=\dfrac{8}{7}\mathrm{AE}^2 \\[4pt]
&=\dfrac{8}{7}(3\sqrt{7})^2 \\[4pt]
&=72
\end{align*}

ヒロ
通常,辺の長さの積を求める場合は方べきの定理を利用するはずなのに使わなかった。

ヒロ
ということは,その部分に何かヒントがありそう。
【スの解答】
$\mathrm{AB}=12$ のとき,$\mathrm{AG}=6$ であるから,$\mathrm{AB}\Cdot\mathrm{AG}=72$ である。よって,
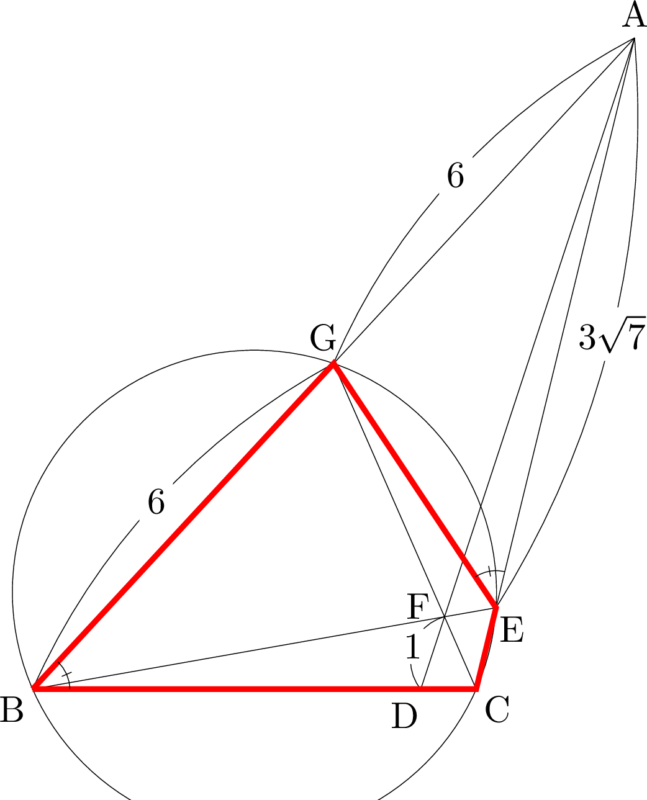
四角形BCEGが円に内接するから,
$\mathrm{AB}=12$ のとき,$\mathrm{AG}=6$ であるから,$\mathrm{AB}\Cdot\mathrm{AG}=72$ である。よって,
\begin{align*}
\mathrm{AB}\Cdota\mathrm{AG}=\mathrm{AE}\Cdota\mathrm{AC}
\end{align*}
が成り立つから,4点B,C,E,Gは同一円周上にある。\mathrm{AB}\Cdota\mathrm{AG}=\mathrm{AE}\Cdota\mathrm{AC}
\end{align*}

四角形BCEGが円に内接するから,
\begin{align*}
\kaku{AEG}=\kaku{ABC}
\end{align*}
である。$\myBox{ス}=②$\kaku{AEG}=\kaku{ABC}
\end{align*}
2020年 センター数学ⅠA 平面図形を解いた感想

ヒロ
前半の「ク」まではかなり楽に解くことができる。

ヒロ
ただチェバの定理やメネラウスの定理を使って式を書く方法だと,意外と時間がかかるかもしれない。

ヒロ
ABの長さを求めるときに,方べきの定理を利用することに気付けるようにしたい。

ヒロ
方べきの定理に目を向けることができれば,それ以降も解きやすくなるだろう。




















