2019年センター試験 数学ⅠA 第2問 三角比の解説をします。
まだ問題を解いていない人は解いてから解説を読んでください。
2019年 センターⅠA 第2問 三角比 $\sankaku{ABC}$ において,$\mathrm{AB}=3$, $\mathrm{BC}=4$, $\mathrm{AC}=2$ とする。
次の $\mybox{エ}$ には,下の⓪~②のうちから当てはまるものを一つ選べ。
$\cos\kaku{BAC}=\dfrac{\myBox{アイ}}{\myBox{ウ}}$ であり,$\kaku{BAC}$ は $\myBox{エ}$ である。
また,$\sin\kaku{BAC}=\dfrac{\sqrt{\myBox{オカ}}}{\myBox{キ}}$ である。
⓪ 鋭角 ① 直角 ② 鈍角
線分ACの垂直二等分線と直線ABの交点をDとする。
$\cos\kaku{CAD}=\dfrac{\myBox{ク}}{\myBox{ケ}}$ であるから,
$\mathrm{AD}=\myBox{コ}$ であり,$\sankaku{DBC}$ の面積は $\dfrac{\myBox{サ}\sqrt{\myBox{シス}}}{\myBox{セ}}$ である。
次の $\mybox{エ}$ には,下の⓪~②のうちから当てはまるものを一つ選べ。
$\cos\kaku{BAC}=\dfrac{\myBox{アイ}}{\myBox{ウ}}$ であり,$\kaku{BAC}$ は $\myBox{エ}$ である。
また,$\sin\kaku{BAC}=\dfrac{\sqrt{\myBox{オカ}}}{\myBox{キ}}$ である。
⓪ 鋭角 ① 直角 ② 鈍角
線分ACの垂直二等分線と直線ABの交点をDとする。
$\cos\kaku{CAD}=\dfrac{\myBox{ク}}{\myBox{ケ}}$ であるから,
$\mathrm{AD}=\myBox{コ}$ であり,$\sankaku{DBC}$ の面積は $\dfrac{\myBox{サ}\sqrt{\myBox{シス}}}{\myBox{セ}}$ である。
考え方と解答

ヒロ
最初は3辺の長さから $\cos$ の値を求める問題。余弦定理を用いて求めよう。

ヒロ
図を描かずに余弦定理の式を書けるようにしよう。
【図を描かずに余弦定理の式を書く方法】
$\cos\kaku{BAC}$ となっている場合,中央の文字が考えている角であるから,$\kaku{A}$ についての余弦定理を考える。余弦定理の式を書くと次のようになっている。
\begin{align*}
\cos\kaku{BAC}=\dfrac{\mathrm{AB}^2+\mathrm{AC}^2-\mathrm{BC}^2}{2\mathrm{AB}\Cdota\mathrm{AC}}
\end{align*}
分母には,中央の文字Aが絡む辺AB,ACを書く。分子には,分母に書いた辺の2乗の和を書いた後,Aが絡まない辺BCの2乗を引けば良い。\cos\kaku{BAC}=\dfrac{\mathrm{AB}^2+\mathrm{AC}^2-\mathrm{BC}^2}{2\mathrm{AB}\Cdota\mathrm{AC}}
\end{align*}

ヒロ
このことはやっている人からすれば当たり前のことなので,出来ていなかった人は出来るようにしよう。
【ア~ウの解答】
余弦定理より
余弦定理より
\begin{align*}
\cos\kaku{BAC}&=\dfrac{3^2+2^2-4^2}{2\Cdota3\Cdota2} \\[4pt]
&=\dfrac{9+4-16}{12} \\[4pt]
&=\dfrac{-3}{12}=\dfrac{-1}{4}
\end{align*}
\cos\kaku{BAC}&=\dfrac{3^2+2^2-4^2}{2\Cdota3\Cdota2} \\[4pt]
&=\dfrac{9+4-16}{12} \\[4pt]
&=\dfrac{-3}{12}=\dfrac{-1}{4}
\end{align*}

ヒロ
$\cos$ の値から鋭角・直角・鈍角を判定する問題。
余弦の符号から分かること$\cos\theta>0$ のとき,$\theta$ は鋭角である。
$\cos\theta=0$ のとき,$\theta$ は直角である。
$\cos\theta<0$ のとき,$\theta$ は鈍角である。
$\cos\theta=0$ のとき,$\theta$ は直角である。
$\cos\theta<0$ のとき,$\theta$ は鈍角である。
【エの解答】 $\cos\kaku{BAC}<0$ より,$\kaku{BAC}$ は鈍角である。$\myBox{エ}=②$

ヒロ
次は余弦の値から正弦の値を求める問題。
【オ~キの解答】 $\sin\kaku{BAC}>0$ より
\begin{align*}
\sin\kaku{BAC}&=\sqrt{1-\left(\dfrac{-1}{4}\right)^2} \\[4pt]
&=\dfrac{\sqrt{15}}{4}
\end{align*}
\sin\kaku{BAC}&=\sqrt{1-\left(\dfrac{-1}{4}\right)^2} \\[4pt]
&=\dfrac{\sqrt{15}}{4}
\end{align*}

ヒロ
次の問題は図を描いて考えよう。
【点Dの位置を把握するための図】
$\cos\kaku{BAC}$ が分かっているため,ABかACを底辺にする。
また,辺ACの垂直二等分線を書くことを考えて,ACを底辺にして図を描く。
ABを描くときに,$\cos\kaku{BAC}=-\dfrac{1}{4}$ であることを意識して描く。
つまり,点Bから直線ACに下ろした垂線の足をHとすると,$\mathrm{AB}:\mathrm{AH}=4:1$ になるように図を描く。
日頃から正確に図を描くことを意識していると,こういうことが苦痛でなくなる。
このような考えで図を描くと,線分ACの垂直二等分線と直線ABの交点Dは次の位置にあることが分かる。
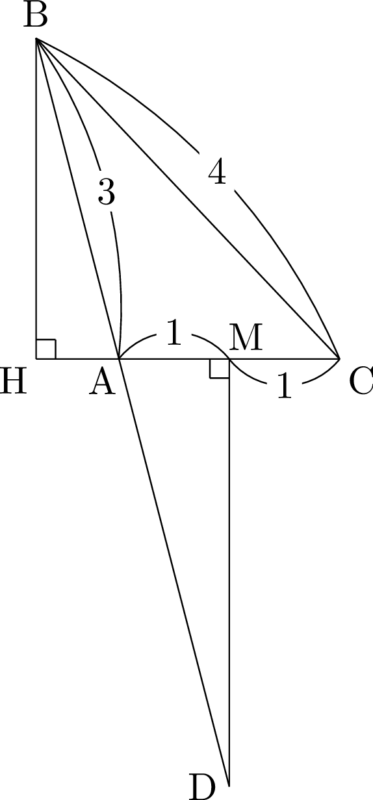
図において,点Dから辺ACに下ろした垂線の足をMとしている。
【クケの解答】
図を見ると,$\kaku{CAD}=180\Deg-\kaku{BAC}$ であることが分かるから,
図を見ると,$\kaku{CAD}=180\Deg-\kaku{BAC}$ であることが分かるから,
\begin{align*}
\cos\kaku{CAD}&=\cos\left(180\Deg-\kaku{BAC}\right) \\[4pt]
&=-\cos\kaku{BAC} \\[4pt]
&=\dfrac{1}{4}
\end{align*}
\cos\kaku{CAD}&=\cos\left(180\Deg-\kaku{BAC}\right) \\[4pt]
&=-\cos\kaku{BAC} \\[4pt]
&=\dfrac{1}{4}
\end{align*}

ヒロ
次はADの長さを求めよう。$\sankaku{ADM}$ に着目するとすぐに求められるはず。
【コの解答】
$\sankaku{ADM}$ において,$\mathrm{AM}=1$ であるから,
$\sankaku{ADM}$ において,$\mathrm{AM}=1$ であるから,
\begin{align*}
&\mathrm{AD}\cos\kaku{CAD}=\mathrm{AM} \\[4pt]
&\dfrac{1}{4}\mathrm{AD}=1 \\[4pt]
&\mathrm{AD}=4
\end{align*}
&\mathrm{AD}\cos\kaku{CAD}=\mathrm{AM} \\[4pt]
&\dfrac{1}{4}\mathrm{AD}=1 \\[4pt]
&\mathrm{AD}=4
\end{align*}

ヒロ
最後は三角形の面積を求める問題。
【サ~セの解答】
図を見ると $\sankaku{DBC}$ は高さが等しい2つの三角形 $\sankaku{CAB}$ と $\sankaku{CAD}$ に分けることができる。
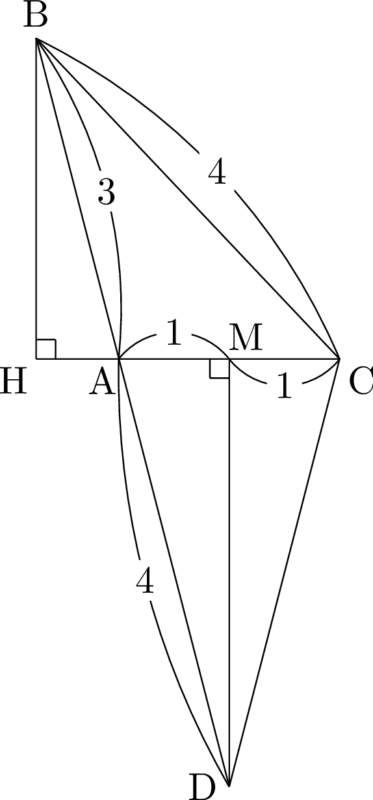
$\mathrm{BD}:\mathrm{AB}=7:3$ より
図を見ると $\sankaku{DBC}$ は高さが等しい2つの三角形 $\sankaku{CAB}$ と $\sankaku{CAD}$ に分けることができる。

$\mathrm{BD}:\mathrm{AB}=7:3$ より
\begin{align*}
\sankaku{DBC}=\dfrac{7}{3}\sankaku{ABC}
\end{align*}
である。ここで,$\sankaku{ABC}$ の面積は\sankaku{DBC}=\dfrac{7}{3}\sankaku{ABC}
\end{align*}
\begin{align*}
\sankaku{ABC}&=\dfrac{1}{2}\Cdota2\Cdota3\Cdota\dfrac{\sqrt{15}}{4}=\dfrac{3\sqrt{15}}{4}
\end{align*}
であるから,\sankaku{ABC}&=\dfrac{1}{2}\Cdota2\Cdota3\Cdota\dfrac{\sqrt{15}}{4}=\dfrac{3\sqrt{15}}{4}
\end{align*}
\begin{align*}
\sankaku{DBC}&=\dfrac{7}{3}\Cdota\dfrac{3\sqrt{15}}{4}=\dfrac{7\sqrt{15}}{4}
\end{align*}
\sankaku{DBC}&=\dfrac{7}{3}\Cdota\dfrac{3\sqrt{15}}{4}=\dfrac{7\sqrt{15}}{4}
\end{align*}
2019年 センター数学ⅠA 三角比を解いた感想

ヒロ
図を描かずに計算できるものについては,できるだけ図を描かなくても求められるようにしよう。

ヒロ
問題量も少なく,比較的易しい問題のため,なるべく速く解けるようにしよう。




















