2018年センター試験 数学ⅡB 第1問 指数関数・対数関数の解説をします。
まだ問題を解いていない人は解いてから解説を読んでください。
2018年 センターⅡB 指数・対数関数$c$ を正の定数として,不等式
3を底とする②の両辺の対数をとり,$t=\log_3x$ とおくと
$c=\sqrt[3]{9}$ のとき,②を満たす $x$ の値の範囲を求めよう。③により
次に,②が $x>\mybox{テ}$ の範囲でつねに成り立つような $c$ の値の範囲を求めよう。
$x$ が $x>\mybox{テ}$ の範囲を動くとき,$t$ のとり得る値の範囲は $\myBox{ニ}$ である。$\myBox{ニ}$ に当てはまるものを,次の⓪~③のうちから一つ選べ。
⓪ 正の実数全体 ① 負の実数全体 ② 実数全体 ③ 1以外の実数全体
この範囲の $t$ に対して,③がつねに成り立つための必要十分条件は,$\log_3c\geqq\dfrac{\myBox{ヌ}}{\myBox{ネ}}$ である。すなわち,$c\geqq\sqrt[\myBox{ノ}]{\myBox{ハヒ}}$ である。
\begin{align*}
x^{\log_3x}\geqq\left(\dfrac{x}{c}\right)^3 \cdots\cdots②
\end{align*}
を考える。x^{\log_3x}\geqq\left(\dfrac{x}{c}\right)^3 \cdots\cdots②
\end{align*}
3を底とする②の両辺の対数をとり,$t=\log_3x$ とおくと
\begin{align*}
t^{~\myBox{ソ}}-\myBox{タ}~t+\mybox{タ}~\log_3c\geqq0 \cdots\cdots③
\end{align*}
となる。ただし,対数 $\log_ab$ に対し,$a$ を底といい,$b$ を真数という。t^{~\myBox{ソ}}-\myBox{タ}~t+\mybox{タ}~\log_3c\geqq0 \cdots\cdots③
\end{align*}
$c=\sqrt[3]{9}$ のとき,②を満たす $x$ の値の範囲を求めよう。③により
\begin{align*}
t\leqq\myBox{チ},~t\geqq\myBox{ツ}
\end{align*}
である。さらに,真数の条件を考えてt\leqq\myBox{チ},~t\geqq\myBox{ツ}
\end{align*}
\begin{align*}
\myBox{テ}<x\leqq\myBox{ト},~x\geqq\myBox{ナ}
\end{align*}
となる。\myBox{テ}<x\leqq\myBox{ト},~x\geqq\myBox{ナ}
\end{align*}
次に,②が $x>\mybox{テ}$ の範囲でつねに成り立つような $c$ の値の範囲を求めよう。
$x$ が $x>\mybox{テ}$ の範囲を動くとき,$t$ のとり得る値の範囲は $\myBox{ニ}$ である。$\myBox{ニ}$ に当てはまるものを,次の⓪~③のうちから一つ選べ。
⓪ 正の実数全体 ① 負の実数全体 ② 実数全体 ③ 1以外の実数全体
この範囲の $t$ に対して,③がつねに成り立つための必要十分条件は,$\log_3c\geqq\dfrac{\myBox{ヌ}}{\myBox{ネ}}$ である。すなわち,$c\geqq\sqrt[\myBox{ノ}]{\myBox{ハヒ}}$ である。
考え方と解答

ヒロ
問題文の誘導通りに,不等式②を対数で表そう。
【ソタの解答】
3を底とする②の両辺の対数をとると
3を底とする②の両辺の対数をとると
\begin{align*}
&\log_3x^{\log_3x}\geqq\log_3\left(\dfrac{x}{c}\right)^3 \\[4pt]
&(\log_3x)^2\geqq3(\log_3x-\log_3c) \\[4pt]
&t^2-3t+3\log_3c\geqq0 \cdots\cdots③
\end{align*}
&\log_3x^{\log_3x}\geqq\log_3\left(\dfrac{x}{c}\right)^3 \\[4pt]
&(\log_3x)^2\geqq3(\log_3x-\log_3c) \\[4pt]
&t^2-3t+3\log_3c\geqq0 \cdots\cdots③
\end{align*}

ヒロ
具体的に与えられた $c$ の値を代入して,③を解こう。
【チツの解答】
$c=\sqrt[3]{9}$ を③に代入すると
$c=\sqrt[3]{9}$ を③に代入すると
\begin{align*}
&t^2-3t+3\log_3\sqrt[3]{9}\geqq0 \\[4pt]
&t^2-3t+3\Cdota\dfrac{2}{3}\geqq0 \\[4pt]
&t^2-3t+2\geqq0 \\[4pt]
&(t-1)(t-2)\geqq0 \\[4pt]
&t\leqq1,~t\geqq2
\end{align*}
&t^2-3t+3\log_3\sqrt[3]{9}\geqq0 \\[4pt]
&t^2-3t+3\Cdota\dfrac{2}{3}\geqq0 \\[4pt]
&t^2-3t+2\geqq0 \\[4pt]
&(t-1)(t-2)\geqq0 \\[4pt]
&t\leqq1,~t\geqq2
\end{align*}

ヒロ
底が1より大きいことを考えて $x$ の値の範囲を求めよう。
【テ~ナの解答】
$x>0$ であり,$t$ は単調に増加するから,
$x>0$ であり,$t$ は単調に増加するから,
\begin{align*}
&\log_3x\leqq1,~\log_3x\geqq2 \\[4pt]
&0<x\leqq3,~x\geqq9
\end{align*}
&\log_3x\leqq1,~\log_3x\geqq2 \\[4pt]
&0<x\leqq3,~x\geqq9
\end{align*}

ヒロ
次は $x$ の値の範囲と $t$ の値の範囲の関係を理解しているか確認する問題。
【ニの解答】
$t=\log_3x$ のグラフを考えると,$x>0$ のとき,$t$ はすべての実数をとり得ることが分かる。よって,$\myBox{ニ}=②$
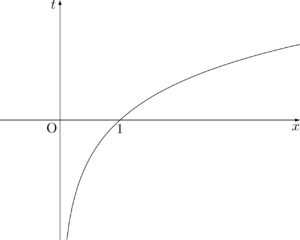
$t=\log_3x$ のグラフを考えると,$x>0$ のとき,$t$ はすべての実数をとり得ることが分かる。よって,$\myBox{ニ}=②$


ヒロ
与えられた範囲で,不等式がつねに成り立つ条件を求める問題。

ヒロ
「つねに $f(x)\geqq0$ が成り立つ」は「$f(x)$ の最小値が0以上」と言い換えることができることを理解しよう。

ヒロ
何でもかんでも判別式がどうのこうのと,意味も分からずに考えるのは辞めよう。
【ヌネの解答】
②が $x>0$ の範囲でつねに成り立つとき,すべての実数 $t$ に対して③が成り立つ。すなわち,$t^2-3t+3\log_3c$ の最小値が0以上になる。このまま最小値を求めても良いし,次のように,さらに考えを進めても良い。これは $t$ の2次方程式
②が $x>0$ の範囲でつねに成り立つとき,すべての実数 $t$ に対して③が成り立つ。すなわち,$t^2-3t+3\log_3c$ の最小値が0以上になる。このまま最小値を求めても良いし,次のように,さらに考えを進めても良い。これは $t$ の2次方程式
\begin{align*}
t^2-3t+3\log_3c=0
\end{align*}
が実数解をもたないということだから,判別式を $D$ とすると,$D\leqq0$ となる。t^2-3t+3\log_3c=0
\end{align*}
\begin{align*}
&9-12\log_3c\leqq0 \\[4pt]
&\log_3c\geqq\dfrac{3}{4}
\end{align*}
&9-12\log_3c\leqq0 \\[4pt]
&\log_3c\geqq\dfrac{3}{4}
\end{align*}

ヒロ
最後は $c$ の範囲を求める問題。
【ノ~ヒの解答】
\begin{align*}
&\log_3c\geqq\dfrac{3}{4} \\[4pt]
&c\geqq3^{\frac{3}{4}} \\[4pt]
&c\geqq\sqrt[4]{27}
\end{align*}
&\log_3c\geqq\dfrac{3}{4} \\[4pt]
&c\geqq3^{\frac{3}{4}} \\[4pt]
&c\geqq\sqrt[4]{27}
\end{align*}
2018年 センター数学IIB 指数関数・対数関数を解いた感想

ヒロ
問題文の誘導通りに進めていくことで,楽に解くことができる。

ヒロ
対数をしっかり理解できているかを問う問題になっている。

ヒロ
また,指数を用いて表された数を累乗根を用いて表すことができるかどうかが問われている。4乗根の4の部分を空欄にするのは珍しい。

ヒロ
特に難しい問題もないため,素早い処理ができるかどうかがポイントとなる。




















