2017年 センター試験 数学ⅠA 第5問 平面図形

2017年センター試験数学ⅠA 第5問平面図形の解説をします。

まだ問題を解いていない人は解いてから解説を読んでください。

2017年センターⅠA 第5問平面図形　$\sankaku{ABC}$ において，$\mathrm{AB}=3$, $\mathrm{BC}=8$, $\mathrm{AC}=7$ とする。
(1) 辺AC上に点Dを $\mathrm{AD}=3$ となるようにとり，$\sankaku{ABD}$ の外接円と直線BCの交点でBと異なるものをEとする。このとき，$\mathrm{BC}\Cdot\mathrm{CE}=\myBox{アイ}$ であるから，$\mathrm{CE}=\dfrac{\myBox{ウ}}{\myBox{エ}}$ である。
　直線ABと直線DEの交点をFとするとき，$\dfrac{\mathrm{BF}}{\mathrm{AF}}=\dfrac{\myBox{オカ}}{\myBox{キ}}$ であるから，$\mathrm{AF}=\dfrac{\myBox{クケ}}{\myBox{コ}}$ である。
(2) $\kaku{ABC}=\myBox{サシ}\Deg$ である。$\sankaku{ABC}$ の内接円の半径は $\dfrac{\myBox{ス}\sqrt{\myBox{セ}}}{\myBox{ソ}}$ であり，$\sankaku{ABC}$ の内心をIとすると $\mathrm{BI}=\dfrac{\myBox{タ}\sqrt{\myBox{チ}}}{\myBox{ツ}}$ である。

Contents

1 (1)の解答
2 (2)の解答
3 2017年センター数学ⅠA 平面図形を解いた感想

(1)の解答

ヒロ

出題されている三角形は有名三角形の1つである「悩み三角形」と分かるから，できるだけ正確に図を描こう。

【点Eの位置を把握するための図を描こう】
「悩み三角形」を描くと次のようになる。$\kaku{B}=60\Deg$ は現時点では関係ないけど，分かるから書いておこう。

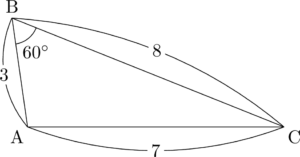
次に点Dをとり，$\sankaku{ABD}$ の外接円を描こう。円を後で描くことになるので難しいけど頑張ろう。$\sankaku{ABD}$ の外接円とBCの交点でBと異なるものがEだから，点Eだと分かるように「E」と書こう。

ヒロ

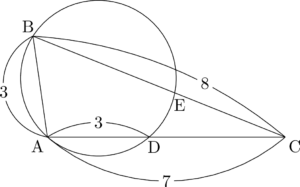
最初は辺の長さの積の値を求める問題。辺の長さの積と来れば方べきの定理。図を見ればこれで解けることも分かる。

【アイの解答】
方べきの定理より

\begin{align*}
\mathrm{BC}\Cdota\mathrm{CE}&=\mathrm{CA}\Cdota\mathrm{CD} \\[4pt]
&=7\Cdota4 \\[4pt]
&=28
\end{align*}

ヒロ

いま求めた等式からCEの長さを求めよう。

【ウエの解答】
$\mathrm{BC}\Cdot\mathrm{CE}=28$ より

\begin{align*}
&8\mathrm{CE}=28 \\[4pt]
&\mathrm{CE}=\dfrac{7}{2}
\end{align*}

ヒロ

次はFの位置を確認しよう。

【点Fの位置を把握するための図を描こう】
直線ABと直線DEの交点Fは，次の図の位置にあることが分かる。

ヒロ

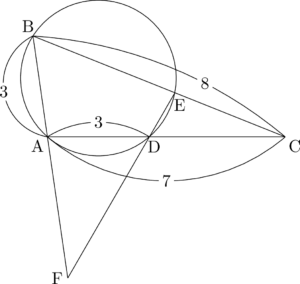
BFとAFの長さの比を求めたいのだから，メネラウスの定理を利用すれば良いね。

【オ～キの解答】
メネラウスの定理より

\begin{align*}
&\dfrac{\mathrm{BF}}{\mathrm{AF}}\Cdot\dfrac{\mathrm{AD}}{\mathrm{DC}}\Cdot\dfrac{\mathrm{CE}}{\mathrm{EB}}=1 \\[4pt]
&\dfrac{\mathrm{BF}}{\mathrm{AF}}\Cdot\dfrac{3}{4}\Cdot\dfrac{\dfrac{7}{2}}{\dfrac{9}{2}}=1 \\[4pt]
&\dfrac{\mathrm{BF}}{\mathrm{AF}}\Cdot\dfrac{3}{4}\Cdot\dfrac{7}{9}=1 \\[4pt]
&\dfrac{\mathrm{BF}}{\mathrm{AF}}=\dfrac{4}{3}\Cdot\dfrac{9}{7} \\[4pt]
&\dfrac{\mathrm{BF}}{\mathrm{AF}}=\dfrac{12}{7}
\end{align*}

(2)の解答

(2) $\kaku{ABC}=\myBox{サシ}\Deg$ である。$\sankaku{ABC}$ の内接円の半径は $\dfrac{\myBox{ス}\sqrt{\myBox{セ}}}{\myBox{ソ}}$ であり，$\sankaku{ABC}$ の内心をIとすると $\mathrm{BI}=\dfrac{\myBox{タ}\sqrt{\myBox{チ}}}{\myBox{ツ}}$ である。

ヒロ

$\kaku{ABC}$ については「悩み三角形」を知っていれば，計算することなく $60\Deg$ であることが分かる。

ヒロ

知らなければ余弦定理で求めよう。

【サシの解答】

\begin{align*}
\cos B&=\dfrac{3^2+8^2-7^2}{2\Cdot3\Cdot8} \\[4pt]
&=\dfrac{9+64-49}{2\Cdot3\Cdot8} \\[4pt]
&=\dfrac{24}{2\Cdot3\Cdot8} \\[4pt]
&=\dfrac{1}{2}
\end{align*}

よって，$\kaku{ABC}=60\Deg$

ヒロ

内接円の半径は三角形の面積を利用して求めよう。

【ス～ソの解答】
$\sankaku{ABC}$ の面積は

\begin{align*}
\sankaku{ABC}&=\dfrac{1}{2}\Cdota3\Cdota8\sin60\Deg \\[4pt]
&=6\sqrt{3}
\end{align*}

であるから，$\sankaku{ABC}$ の内接円の半径を $r$ とすると

\begin{align*}
&\dfrac{1}{2}(3+8+7)r=6\sqrt{3} \\[4pt]
&9r=6\sqrt{3} \\[4pt]
&r=\dfrac{2\sqrt{3}}{3}
\end{align*}

ヒロ

$\sankaku{ABC}$ の内接円がどんな状態かを確認しておこう。

【BIがどの部分かを確認するための図を描こう】
$\sankaku{ABC}$ の内心Iから辺ABに下ろした垂線の足をHとすると，$\sankaku{IBH}$ は直角三角形になる。

ヒロ

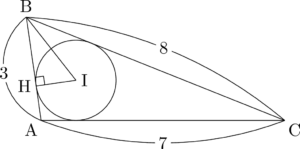
ここで，内心は3つの内角の二等分線の交点であるから，$\kaku{IBH}=30\Deg$ であることに気付けるようにしよう。

【タ～ツの解答】
$\sankaku{IBH}$ は $1:2:\sqrt{3}$ の有名直角三角形であるから，

\begin{align*}
\mathrm{BI}&=2\mathrm{IH} \\[4pt]
&=2r \\[4pt]
&=\dfrac{4\sqrt{2}}{3}
\end{align*}

ヒロ

$\sankaku{IBH}$ が有名直角三角形であることに気付けなかった場合は，BHの長さを求めて三平方の定理を使うことになるだろう。

ヒロ

その場合は接線の長さを公式として覚えていれば速く計算できる。

【タ～ツの別解】
BHの長さはBから $\sankaku{ABC}$ の内接円に引いた接線の長さだから

\begin{align*}
\mathrm{BH}&=\dfrac{3+8-7}{2}=2
\end{align*}

よって，

\begin{align*}
\mathrm{BI}&=\sqrt{2^2+\left(\dfrac{2\sqrt{3}}{3}\right)^2} \\[4pt]
&=\dfrac{2}{3}\sqrt{3^2+(\sqrt{3})^2} \\[4pt]
&=\dfrac{4\sqrt{2}}{3}
\end{align*}