ここでは三角比を含む不等式について解説します。
三角比を含む方程式を解けることを前提にしているため,知識があやふやな人は次の記事を読んでください。
サインはy座標,コサインはx座標,タンジェントは傾きの範囲を意識しましょう。
特にタンジェントについては,90°では定義されないことに注意しましょう。
三角比を含む不等式の問題
問題$0\Deg\leqq\theta\leqq180\Deg$ とする。次の不等式を満たす $\theta$ の値の範囲を求めよ。
(1) $\sin\theta>\dfrac{\sqrt{3}}{2}$
(2) $\cos\theta\leqq-\dfrac{1}{\sqrt{2}}$
(3) $0\leqq\tan\theta\leqq\dfrac{1}{\sqrt{3}}$
(1) $\sin\theta>\dfrac{\sqrt{3}}{2}$
(2) $\cos\theta\leqq-\dfrac{1}{\sqrt{2}}$
(3) $0\leqq\tan\theta\leqq\dfrac{1}{\sqrt{3}}$
【(1)の考え方と解答】
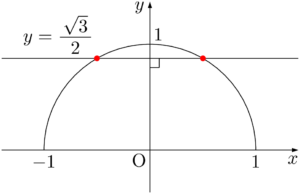
まず,半円上の点で $y$ 座標が $\dfrac{\sqrt{3}}{2}$ である点を探そう。次の図の赤い2つの点を見つけることができる。
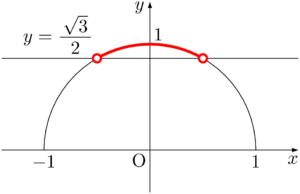
解くべき不等式は $\sin\theta>\dfrac{\sqrt{3}}{2}$ であるから,半円上で $y$ 座標が $\dfrac{\sqrt{3}}{2}$ より大きくなる場所を考えると,次の図の赤線部分であることが分かる。
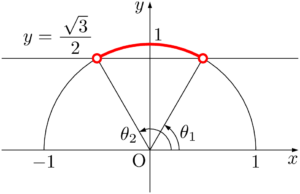
あとは $x$ 軸の正の方向とのなす角の範囲を考えよう。図のように $\theta_1,~\theta_2$ を定めると,不等式の解は $\theta_1<\theta<\theta_2$ となる。$\theta_1,~\theta_2$ を求めれば終わりだね。
まず,半円上の点で $y$ 座標が $\dfrac{\sqrt{3}}{2}$ である点を探そう。次の図の赤い2つの点を見つけることができる。

解くべき不等式は $\sin\theta>\dfrac{\sqrt{3}}{2}$ であるから,半円上で $y$ 座標が $\dfrac{\sqrt{3}}{2}$ より大きくなる場所を考えると,次の図の赤線部分であることが分かる。

あとは $x$ 軸の正の方向とのなす角の範囲を考えよう。図のように $\theta_1,~\theta_2$ を定めると,不等式の解は $\theta_1<\theta<\theta_2$ となる。$\theta_1,~\theta_2$ を求めれば終わりだね。

$\theta_1=60\Deg,~\theta_2=120\Deg$ であるから,求める不等式の解は
\begin{align*}60\Deg<\theta<120\Deg \end{align*}
(2) $\cos\theta\leqq-\dfrac{1}{\sqrt{2}}$
【(2)の考え方と解答】
まず,半円上の点で $x$ 座標が $-\dfrac{1}{\sqrt{2}}$ である点を探そう。次の図の赤い点が見つかる。
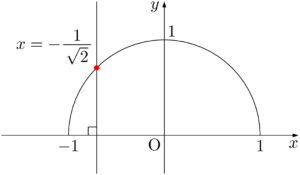

解くべき不等式は $\cos\theta\leqq-\dfrac{1}{\sqrt{2}}$ であるから,半円上で $x$ 座標が $-\dfrac{1}{\sqrt{2}}$ 以下になる場所を考えると,次の図の赤線部分であることが分かる。
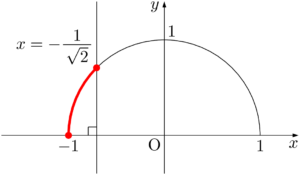
あとは $x$ 軸の正の方向とのなす角の範囲を考えよう。図のように $\theta_1$ を定めると,不等式の解は $\theta_1\leqq\theta\leqq180\Deg$ となる。$\theta_1$ を求めれば終わりだね。
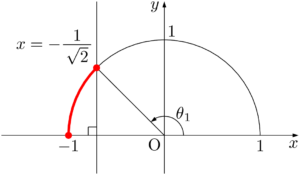

あとは $x$ 軸の正の方向とのなす角の範囲を考えよう。図のように $\theta_1$ を定めると,不等式の解は $\theta_1\leqq\theta\leqq180\Deg$ となる。$\theta_1$ を求めれば終わりだね。

$\theta_1=135\Deg$ であるから,求める不等式の解は
\begin{align*} 135\Deg\leqq\theta\leqq180\Deg \end{align*}
(3) $0\leqq\tan\theta\leqq\dfrac{1}{\sqrt{3}}$
【(3)の考え方と解答】
まず,直線 $y=\dfrac{1}{\sqrt{3}}x$ を描こう。
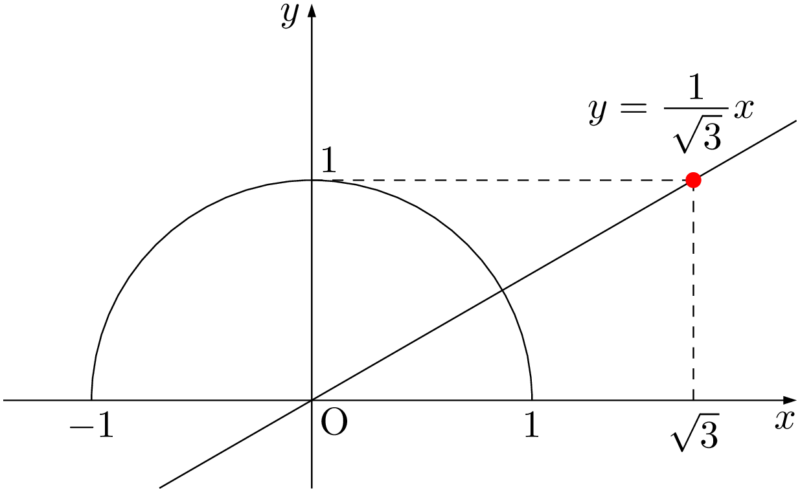

解くべき不等式は $0\leqq\tan\theta\leqq\dfrac{1}{\sqrt{3}}$ であるから,半円上で原点と結んだ線分の傾きが0以上 $\dfrac{1}{\sqrt{3}}$ 以下である場所を考えると,次の図の赤線部分であることが分かる。
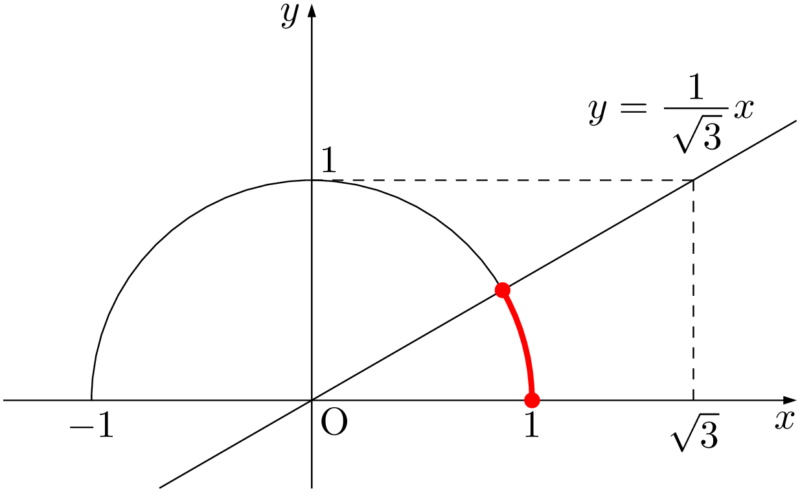

$x$ 軸の正の方向とのなす角の範囲を考えよう。図のように $\theta_1$ を定めると,不等式の解は $0\Deg\leqq\theta\leqq\theta_1$ となる。
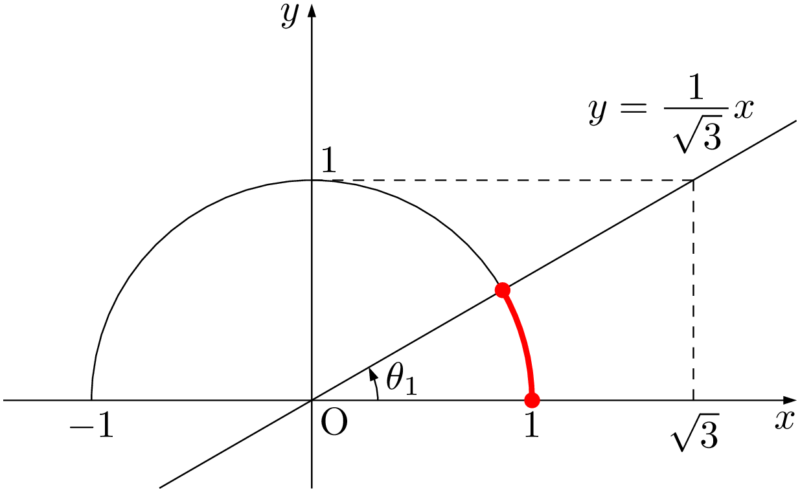

$\theta_1=30\Deg$ であるから,求める不等式の解は
\begin{align*} 0\Deg\leqq\theta\leqq30\Deg \end{align*}
三角比を含む不等式の問題2
問題$0\Deg\leqq\theta\leqq180\Deg$ とする。次の不等式を満たす $\theta$ の値の範囲を求めよ。
(1) $\sin\theta\leqq\dfrac{1}{2}$
(2) $-\dfrac{\sqrt{3}}{2}\leqq\cos\theta<\dfrac{1}{2}$ (3) $\dfrac{1}{\sqrt{3}}\leqq\tan\theta<\sqrt{3}$
(1) $\sin\theta\leqq\dfrac{1}{2}$
(2) $-\dfrac{\sqrt{3}}{2}\leqq\cos\theta<\dfrac{1}{2}$ (3) $\dfrac{1}{\sqrt{3}}\leqq\tan\theta<\sqrt{3}$
【(1)の考え方と解答】
原点を中心とする半径1の半円(上半分)を利用しよう。$y$ 座標が $\dfrac{1}{2}$ 以下の部分は図の赤線部分である。
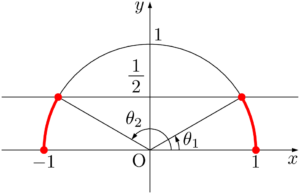
赤線部分が2か所に分かれるから,角 $\theta$ の範囲も2つに分けて書こう。$\theta_1=30\Deg,~\theta_2=150\Deg$ より,求める不等式の解は
原点を中心とする半径1の半円(上半分)を利用しよう。$y$ 座標が $\dfrac{1}{2}$ 以下の部分は図の赤線部分である。

赤線部分が2か所に分かれるから,角 $\theta$ の範囲も2つに分けて書こう。$\theta_1=30\Deg,~\theta_2=150\Deg$ より,求める不等式の解は
\begin{align*} 0\Deg\leqq\theta\leqq30\Deg,~150\Deg\leqq\theta\leqq180\Deg \end{align*}
(2) $-\dfrac{\sqrt{3}}{2}\leqq\cos\theta<\dfrac{1}{2}$
【(2)の考え方と解答】
半円上で $x$ 座標が $-\dfrac{\sqrt{3}}{2}$ 以上 $\dfrac{1}{2}$ 未満の部分を考えると,次の図の赤線部分となる。
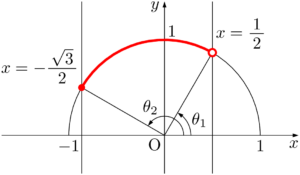
$\theta_1=60\Deg,~\theta_2=150\Deg$ である。$\theta_1$ は解に含まれず,$\theta_2$ は解に含まれることに注意して,求める不等式の解は
半円上で $x$ 座標が $-\dfrac{\sqrt{3}}{2}$ 以上 $\dfrac{1}{2}$ 未満の部分を考えると,次の図の赤線部分となる。

$\theta_1=60\Deg,~\theta_2=150\Deg$ である。$\theta_1$ は解に含まれず,$\theta_2$ は解に含まれることに注意して,求める不等式の解は
\begin{align*} 60\Deg<\theta\leqq150\Deg \end{align*}
(3) $\dfrac{1}{\sqrt{3}}\leqq\tan\theta<\sqrt{3}$
【(3)の考え方と解答】
半円上の点と原点を結ぶ直線の傾きが $\dfrac{1}{\sqrt{3}}$ 以上 $\sqrt{3}$ 未満の部分を考えると,次の図の赤線部分となる。
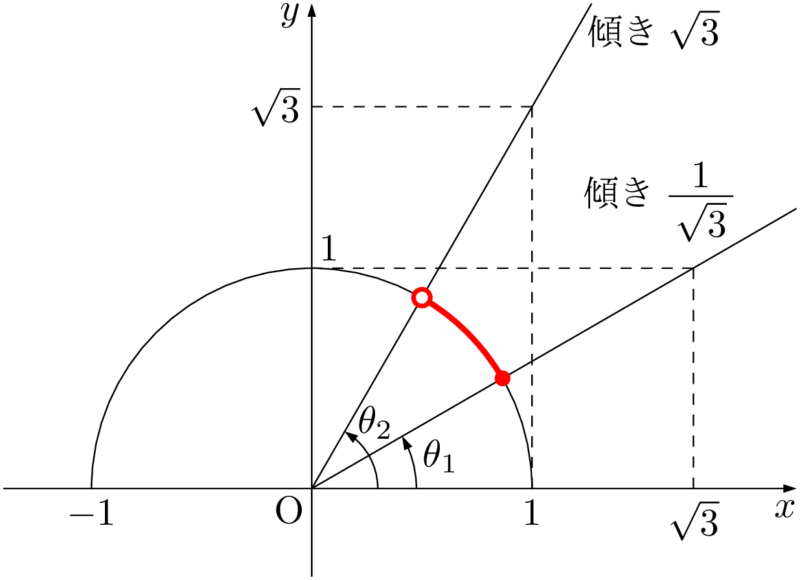
$\theta_1=30\Deg,~\theta_2=60\Deg$ であるから,求める不等式の解は
半円上の点と原点を結ぶ直線の傾きが $\dfrac{1}{\sqrt{3}}$ 以上 $\sqrt{3}$ 未満の部分を考えると,次の図の赤線部分となる。

$\theta_1=30\Deg,~\theta_2=60\Deg$ であるから,求める不等式の解は
\begin{align*} 30\Deg\leqq\theta<60\Deg \end{align*}
三角比を含む不等式の問題3
問題$0\Deg\leqq\theta\leqq180\Deg$ とする。次の不等式を満たす $\theta$ の値の範囲を求めよ。
(1) $\dfrac{1}{2}<\sin\theta\leqq\dfrac{\sqrt{3}}{2}$ (2) $\cos\theta\geqq-\dfrac{1}{2}$ (3) $\tan\theta\leqq1$
(1) $\dfrac{1}{2}<\sin\theta\leqq\dfrac{\sqrt{3}}{2}$ (2) $\cos\theta\geqq-\dfrac{1}{2}$ (3) $\tan\theta\leqq1$
【(1)の考え方と解答】
原点中心,半径1の半円上で $y$ 座標が $\dfrac{1}{2}$ より大きく $\dfrac{\sqrt{3}}{2}$ 以下の部分を考えると,次の図の赤線部分となる。
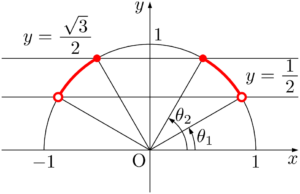
$\theta_1=30\Deg,~\theta_2=60\Deg$ である。$y$ 軸に対称であることと,含まれる角と含まれない角に注意すると,求める不等式の解は

$\theta_1=30\Deg,~\theta_2=60\Deg$ である。$y$ 軸に対称であることと,含まれる角と含まれない角に注意すると,求める不等式の解は
\begin{align*} 30\Deg<\theta\leqq60\Deg,~120\Deg\leqq\theta<150\Deg \end{align*}
(2) $\cos\theta\geqq-\dfrac{1}{2}$
【(2)の考え方と解答】
半円上で $x$ 座標が $-\dfrac{1}{2}$ 以上の部分を考えると,次の図の赤線部分となる。
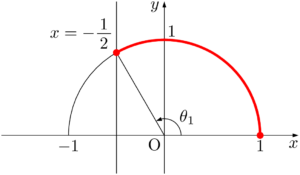
$\theta_1=120\Deg$ であるから,求める不等式の解は
半円上で $x$ 座標が $-\dfrac{1}{2}$ 以上の部分を考えると,次の図の赤線部分となる。

$\theta_1=120\Deg$ であるから,求める不等式の解は
\begin{align*} 0\Deg\leqq\theta\leqq120\Deg \end{align*}
(3) $\tan\theta\leqq1$
【(3)の考え方と解答】
半円上の点と原点を結ぶ直線の傾きが1以下の部分を考えると,次の図の赤線部分となる。
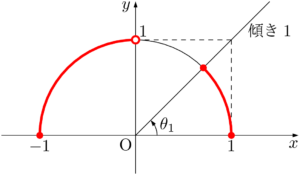
ここで注意したいのは第2象限の部分である。「傾きが1以下」というのは傾きが負である場合も含まれているため,第2象限の点も解に含まれる。また,90°のタンジェントは定義されていないため,90°の点 $(0,~1)$ は常に除外される。 $\theta_1=45\Deg$ であるから,求める不等式の解は
半円上の点と原点を結ぶ直線の傾きが1以下の部分を考えると,次の図の赤線部分となる。

ここで注意したいのは第2象限の部分である。「傾きが1以下」というのは傾きが負である場合も含まれているため,第2象限の点も解に含まれる。また,90°のタンジェントは定義されていないため,90°の点 $(0,~1)$ は常に除外される。 $\theta_1=45\Deg$ であるから,求める不等式の解は
\begin{align*} 0\Deg\leqq\theta<45\Deg,~90\Deg<\theta\leqq180\Deg \end{align*}



















