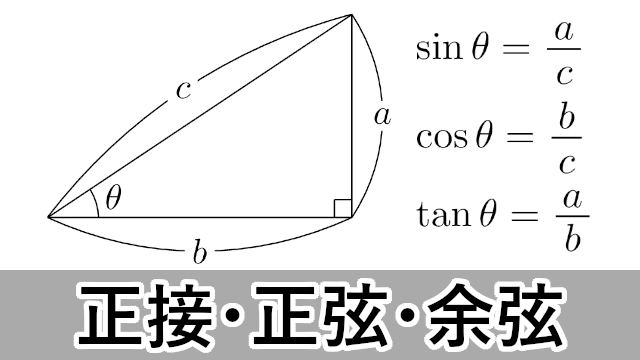
ここでは三角比について説明します。
三角比には,サイン・コサイン・タンジェントの3つがあります。
三角比をうまく利用することで,木の高さなどを調べることができます。
「そんなの調べないよ~」と言う人もいますが,「木の高さを調べる」というのは,話を単純化させた一つの例であって,国家資格でもある測量士が行う「測量」において三角比が役に立っています。
初めて出てくる記号や考え方を正しく理解して使えるようになりましょう。
正接・正弦・余弦
【正接・正弦・余弦とは】
次の図において,2つの半直線OA,OBのなす角 $\theta$(シータと読むギリシャ文字) は鋭角であるとする。$\kaku{AOB}$ の辺OA上の2点P,P’ から辺OBに,それぞれ垂線PQ,P’Q’ を下ろすと
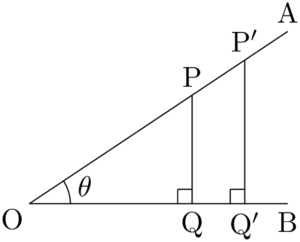
対応する辺の長さの比が等しいから
また,同じように他の2辺の比 $\dfrac{\text{PQ}}{\text{OP}},~\dfrac{\text{OQ}}{\text{OP}}$ の値も辺OA上の点Pの位置に関係なく,角 $\theta$ によってのみ定まる。
$\dfrac{\text{PQ}}{\text{OP}}$ を角 $\theta$ の正弦またはサインといい,$\sin\theta$ と表し,$\dfrac{\text{OQ}}{\text{OP}}$ を角 $\theta$ の余弦またはコサインといい,$\cos\theta$ と表す。
次の図において,2つの半直線OA,OBのなす角 $\theta$(シータと読むギリシャ文字) は鋭角であるとする。$\kaku{AOB}$ の辺OA上の2点P,P’ から辺OBに,それぞれ垂線PQ,P’Q’ を下ろすと
\begin{align*}
\sankaku{POQ}∽\sankaku{P’OQ’}
\end{align*}
\sankaku{POQ}∽\sankaku{P’OQ’}
\end{align*}

対応する辺の長さの比が等しいから
\begin{align*}
\text{PQ}:\text{OQ}=\text{P$’$Q$’$}:\text{OQ$’$}
\end{align*}
となる。したがって\text{PQ}:\text{OQ}=\text{P$’$Q$’$}:\text{OQ$’$}
\end{align*}
\begin{align*}
\dfrac{\text{PQ}}{\text{OQ}}=\dfrac{\text{P$’$Q$’$}}{\text{OQ$’$}}
\end{align*}
が成り立つ。このことから $\dfrac{\text{PQ}}{\text{OQ}}$ の値は辺OA上の点Pの位置に関係なく,$\theta$ だけによって定まることが分かる。この $\dfrac{\text{PQ}}{\text{OQ}}$ を角 $\theta$ の正接またはタンジェントといい,$\tan\theta$ と表す。\dfrac{\text{PQ}}{\text{OQ}}=\dfrac{\text{P$’$Q$’$}}{\text{OQ$’$}}
\end{align*}
また,同じように他の2辺の比 $\dfrac{\text{PQ}}{\text{OP}},~\dfrac{\text{OQ}}{\text{OP}}$ の値も辺OA上の点Pの位置に関係なく,角 $\theta$ によってのみ定まる。
$\dfrac{\text{PQ}}{\text{OP}}$ を角 $\theta$ の正弦またはサインといい,$\sin\theta$ と表し,$\dfrac{\text{OQ}}{\text{OP}}$ を角 $\theta$ の余弦またはコサインといい,$\cos\theta$ と表す。
三角比

ヒロ
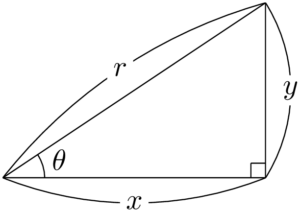
正接・正弦・余弦をまとめて三角比という。
三角比図の直角三角形において
\begin{align*}
&\sin\theta=\dfrac{y}{r} \\[4pt]
&\cos\theta=\dfrac{x}{r} \\[4pt]
&\tan\theta=\dfrac{y}{x}
\end{align*}
&\sin\theta=\dfrac{y}{r} \\[4pt]
&\cos\theta=\dfrac{x}{r} \\[4pt]
&\tan\theta=\dfrac{y}{x}
\end{align*}

三角比の値を求める練習問題

ヒロ
実際に定期テストで出題された問題を解いてみよう。
問題下の図において,$\sin\theta,~\cos\theta,~\tan\theta$ の値を,それぞれ求めよ。
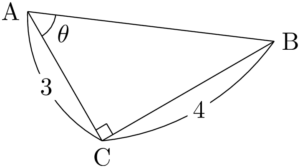

【考え方と解答】
着目している角 $\theta$ と直角の位置に注意して求めよう。次の図のように,直角を右側に,$\theta$ が左側になるようにして考えよう。
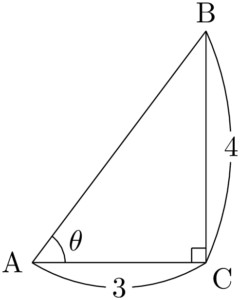
三平方の定理より
着目している角 $\theta$ と直角の位置に注意して求めよう。次の図のように,直角を右側に,$\theta$ が左側になるようにして考えよう。

三平方の定理より
\begin{align*}
&\text{AB}^2=3^2+4^2=25 \\[4pt]
&\text{AB}=5
\end{align*}
よって,&\text{AB}^2=3^2+4^2=25 \\[4pt]
&\text{AB}=5
\end{align*}
\begin{align*}
&\sin\theta=\dfrac{\text{BC}}{\text{AB}}=\dfrac{4}{5} \\[4pt]
&\cos\theta=\dfrac{\text{AC}}{\text{AB}}=\dfrac{3}{5} \\[4pt]
&\tan\theta=\dfrac{\text{BC}}{\text{AC}}=\dfrac{4}{3}
\end{align*}
&\sin\theta=\dfrac{\text{BC}}{\text{AB}}=\dfrac{4}{5} \\[4pt]
&\cos\theta=\dfrac{\text{AC}}{\text{AB}}=\dfrac{3}{5} \\[4pt]
&\tan\theta=\dfrac{\text{BC}}{\text{AC}}=\dfrac{4}{3}
\end{align*}
三角形の角と対辺

ヒロ
三角形の角と対辺の表し方について知っておこう。
【三角形の角と対辺】
次の図のような三角形ABCを考える。
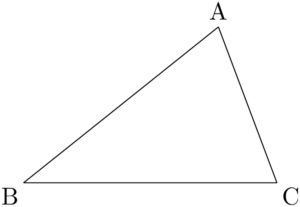
このとき $\kaku{BAC}$ を $A$ と表す。同様に,$\kaku{ABC}=B$, $\kaku{BCA}=C$ と表す。また,辺の長さについては,BCの長さは頂点Aの対辺であるから $a$ と表す。同様に $\text{CA}=b,~\text{AB}=c$ と表す。

次の図のような三角形ABCを考える。

このとき $\kaku{BAC}$ を $A$ と表す。同様に,$\kaku{ABC}=B$, $\kaku{BCA}=C$ と表す。また,辺の長さについては,BCの長さは頂点Aの対辺であるから $a$ と表す。同様に $\text{CA}=b,~\text{AB}=c$ と表す。


ヒロ
問題で決められているときは,このように設定されていることが多い。

ヒロ
自分で決めるときも,できるだけこのように設定することが好まれる。
三角比の値を求める練習問題2

ヒロ
実際に定期テストで出題された問題を解いてみよう。
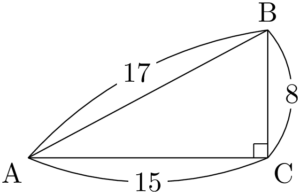
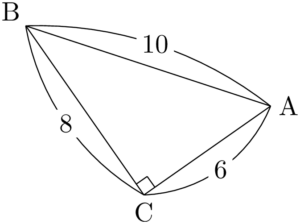
問題次の直角三角形において $\sin A,~\cos A,~\tan A$ の値を求めよ。
(1)
(2)
(1)

(2)

【(1)の考え方と解答】
$A$ が左側にあり,直角が右側にあるから,このまま考えれば良い。
$A$ が左側にあり,直角が右側にあるから,このまま考えれば良い。
\begin{align*}
&\sin A=\dfrac{8}{17} \\[4pt]
&\cos A=\dfrac{15}{17} \\[4pt]
&\tan A=\dfrac{8}{15}
\end{align*}
&\sin A=\dfrac{8}{17} \\[4pt]
&\cos A=\dfrac{15}{17} \\[4pt]
&\tan A=\dfrac{8}{15}
\end{align*}
【(2)の考え方と解答】
$A$ が左側に,直角が右側にあるように向きを変えよう。
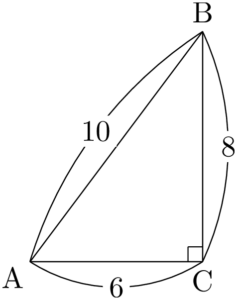
$A$ が左側に,直角が右側にあるように向きを変えよう。

\begin{align*}
&\sin A=\dfrac{8}{10}=\dfrac{4}{5} \\[4pt]
&\cos A=\dfrac{6}{10}=\dfrac{3}{5} \\[4pt]
&\tan A=\dfrac{8}{6}=\dfrac{4}{3}
\end{align*}
&\sin A=\dfrac{8}{10}=\dfrac{4}{5} \\[4pt]
&\cos A=\dfrac{6}{10}=\dfrac{3}{5} \\[4pt]
&\tan A=\dfrac{8}{6}=\dfrac{4}{3}
\end{align*}
今回は三角形の向きを変えて三角比の値を求めているが,向きを変えずに求められるようになろう。