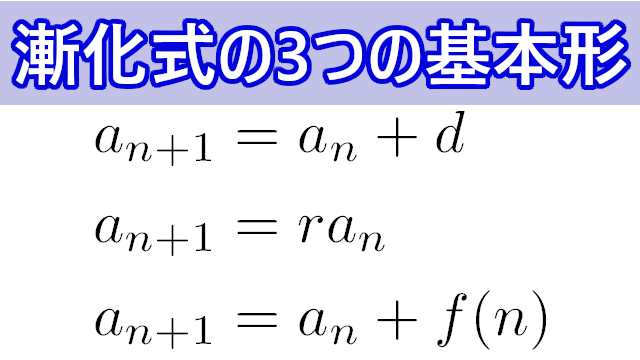一般項を求める様々な漸化式の問題の基礎となる3つの基本形をマスターしましょう！ほとんどの問題において，漸化式を解くときは3つの基本形のいずれかに帰着させるため，絶対にマスターしなければなりません。
次の3つの形の問題を解けるようになることが目標です。
2. $~a_{n+1}=ra_n$
3. $~a_{n+1}=a_n+f(n)$
プリントを次のリンクからダウンロードできます。
どのタイプの漸化式でもそうですが，意味も理解しないまま，ただ単に式の形と解法を結びつけて覚えてもすぐに忘れてしまいます。
そうならないためにも，しっかりと意味を理解することが重要です。
等差型の漸化式の解法
まずは $a_{n+1}=a_n+d$ の式の意味を捉えよう。
&a_2=a_1+d \\[4pt]&a_3=a_2+d \\[4pt]&a_4=a_3+d
\end{align*}
ここから次のことが分かる。
第2項に $d$ を加えると 第3項になる。
第3項に $d$ を加えると 第4項になる。
最初に与えられた漸化式をもう一度確認すると，「第 $n$ 項に $d$ を加えると，第 $n+1$ 項になる」と分かるね。
つまり，数列 $\{a_n\}$ の各項を並べると次のようになる。
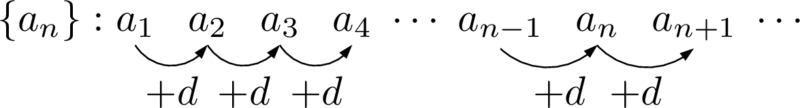
では，第 $n$ 項の $a_n$ は初項 $a_1$ に $d$ を何個加えたものか分かるかな？
$a_3$ なら $a_1$ に $d$ を2個加えたものになってて，$a_4$ なら $a_1$ に $d$ を3個加えたものになってるから，$a_n$ は $a_1$ に $d$ を $n-1$ 個加えたものですね。
$n$ 個だと勘違いしないようにしよう。一般項はどうなる？
$a_n=a_1+d(n-1)$ になります。
いいね。隣り合う2項の差が等しい数列を等差数列といって，その差のことを公差ということも覚えておこう。
初項 $a$，公差 $d$ の等差数列の一般項 $a_n$ は
a_n=a+d(n-1)
\end{align*}
(等差数列の和)=\dfrac{(初項)+(末項)}{2}\times(項数)
\end{align*}
例えば，等差数列 $\{a_n\}$ の第10項から第30項までの和 $S$ を求める場合，$a_{10}$ を初項と考えればよいから，
S=\dfrac{a_{10}+a_{30}}{2}\times21
\end{align*}
また，公差が0のときは，漸化式は $\bm{a_{n+1}=a_n}$ となり，$\bm{a_1}$ がずっと並ぶ定数列であるから，その和 $S$ は
S=a_1\times(項数)
\end{align*}
等比型の漸化式の解法
等差型と同じようにして $a_{n+1}=ra_n$ の式の意味を捉えよう。
&a_2=ra_1 \\[4pt]&a_3=ra_2 \\[4pt]&a_4=ra_3
\end{align*}
ここから次のことが分かる。
第2項に $r$ を掛けると 第3項になる。
第3項に $r$ を掛けると 第4項になる。
最初に与えられた漸化式をもう一度確認すると，「第 $n$ 項に $r$ を掛けると，第 $n+1$ 項になる」と分かるね。
つまり，数列 $\{a_n\}$ の各項を並べると次のようになる。
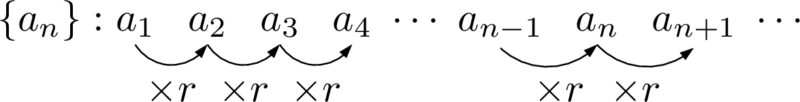
では，第 $n$ 項の $a_n$ は初項 $a_1$ に $r$ を何個掛けたものか分かるかな？
$a_3$ なら $a_1$ に $r$ を2個掛けたものになってて，$a_3$ なら $a_1$ に $r$ を3個掛けたものになってるから，$a_n$ は $a_1$ に $r$ を $n-1$ 個掛けたものですね。
$n$ 個だと勘違いしないようにしよう。一般項はどうなる？
$a_n=a_1\Cdot r^{n-1}$ になります。
いいね。隣り合う2項の比が等しい数列を等比数列といって，その比のことを公比ということも覚えておこう。
初項 $a$，公比 $r$ の等比数列の一般項 $a_n$ は
a_n=a\Cdota r^{n-1}
\end{align*}
(等比数列の和)=\dfrac{(初項)\times\{(公比)^{(項数)}-1\}}{(公比)-1}
\end{align*}
例えば，公比 $r~(\neq1)$ の等比数列 $\{a_n\}$ の第10項から第30項までの和 $S$ を求める場合，$a_{10}$ を初項と考えればよいから，
(等比数列の和)=\dfrac{a_{10}\times(r^{21}-1)}{r-1}
\end{align*}
また，公比が1のとき，数列 $\{a_n\}$ は $a_1$ がずっと並ぶ定数列となる。
階差型の漸化式の解法
これまでと同様に $a_{n+1}=a_n+f(n)$ の式の意味を捉えよう。
&a_2=a_1+f(1) \\[4pt]&a_3=a_2+f(2) \\[4pt]&a_4=a_3+f(3)
\end{align*}
ここから次のことが分かる。
第2項に $f(2)$ を加えると 第3項になる。
第3項に $f(3)$ を加えると 第4項になる。
最初に与えられた漸化式をもう一度確認すると，「第 $n$ 項に $f(n)$ を加えると，第 $n+1$ 項になる」と分かるね。
つまり，数列 $\{a_n\}$ の各項を並べると次のようになる。
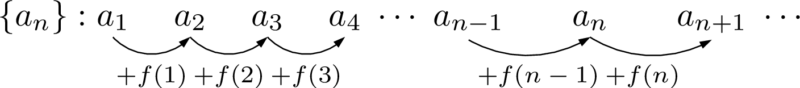
等差数列とは違って，加える値が変わっていくことに注意しよう。第 $n$ 項は初項 $a_1$ に $f(1),f(2),\cdots,f(n-1)$ を加えたものになってるね。$f(n)$ まで加えるのではなく，$f(n-1)$ まで加えたものになってることに注意しよう。
ここで，$n=1$ のときは「 $f(1)$ から $f(0)$ まで加える」となって意味が分からなくなるため，この考え方は $n\geqq2$ のときに成り立ち，一般項は $a_n=a_1+\Sum{k=1}{n-1}f(k)$ となる。
一般項を求めた後，$n=1$ のときに成り立つかどうかを確かめよう。また，シグマの中に入れるときに $\bm{f(n)}$ の $\bm{n}$ を $\bm{k}$ にするのを忘れて $\bm{\Sum{k=1}{n-1}f({\color{red}n})}$ と書いてしまうことのないように，$\bm{f(k)}$ の $\bm{k}$ に $\bm{1,2,\cdots}$ と代入して足してるんだと意味を考えて書くようにしよう。
隣り合う2項の差が作る数列を階差数列ということも覚えておこう。
初項 $a$，階差数列の一般項が $f(n)$ である数列の一般項 $a_n$ は $n\geqq2$ のとき
a_n=a+\Sum{k=1}{n-1}f(k)
\end{align*}
漸化式の基本形である3つのタイプの練習
それでは練習しておこう。
答え合わせをしよう。
&a_n=3+4(n-1) \\[4pt]&a_n=4n-1
\end{align*}
楽勝です！
a_n&=2+\Sum{k=1}{n-1}6k^2 \\[4pt]&=2+6\Cdota\dfrac{1}{6}(n-1)n(2n-1) \\[4pt]&=2n^3-3n^2+n+2
\end{align*}
シグマの公式を覚えてて，$n-1$の部分を間違えなければ余裕です！
実際には，「 $n=1$ を代入して，$a_1=2-3+1+2=2$ となるから $n=1$ のときも成り立つ」わけだけど，解答にはこんなに丁寧に書かなくても良いよ。
あとシグマ公式の部分についてちょっと言っとこうか。
\Sum{k=1}{n}k^2=\dfrac{1}{6}n(n+1)(2n+1)
\end{align*}
(n-1)+n=2n-1
\end{align*}
なるほど。「2倍して1を足す」から「既に書いている2数を足す」に解釈を変えるんですね。単純ですけど，計算回数が2回から1回になるので速くなりそうです。
あと，もう一か所，計算方法について言っとくよ。
$(n-1)n(2n-1)$ の展開については左から順にするのではなく，$(n-1)(2n-1)$ の展開を考えて，各項の次数を1つ上げれば良い。これで暗算で展開できるはず。
なるほど。$(n-1)(2n-1)=2n^2-3n+1$ は暗算でできますからね。$n$ の指数を書くときに1だけ大きくすれば良いってことですね！
そういうこと！
a_n&=3+\Sum{k=1}{n-1}(2^k+3k) \\[4pt]&=3+\dfrac{2(2^{n-1}-1)}{2-1}+3\Cdota\dfrac{1}{2}(n-1)n \\[4pt]&=2^n+\dfrac{3}{2}n^2-\dfrac{3}{2}n+1
\end{align*}
$\Sum{k=1}{n-1}2^k$ の部分については，公式を丸暗記してる人もいるけど，シグマの公式として覚える必要は全くないからね。書き並べれば簡単に分かるはず。
\Sum{k=1}{n-1}2^k&=2+2^2+2^3+\cdots+2^{n-1} \\[4pt]&=(初項2，公比2，項数 n-1 の等比数列の和) \\[4pt]&=\dfrac{2(2^{n-1}-1)}{2-1} \\[4pt]&=2^n-2
\end{align*}
まとめ
等差型・等比型については，そのまま出題したのでは簡単すぎて入試の意味をなさないため，実際には，少し形を変えて出題されることがほとんどだ。
ここで扱った3つのタイプの漸化式はすべての基本となる形なので，しっかりと理解して解けるようにしよう。
