ここではトレミーの定理について説明します。
大学入試問題では,「トレミーの定理」という定理の名前が出ることは少ないですが,その定理の証明は出題されます。
そのため,トレミーの定理を知っているかどうかではなく,証明できるかどうかがポイントとなります。
しかし,私大入試などにある答えだけを書けば良い形式の試験では,トレミーの定理を利用することで時短することができるため時間的に有利になります。
トレミーの定理

ヒロ
トレミーの定理とは次のようなものである。
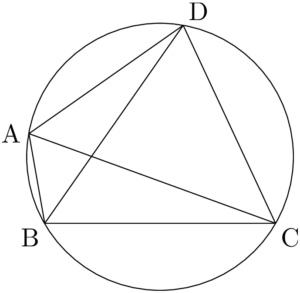
トレミーの定理円周上に4点A,B,C,Dがあるとき,
\begin{align*}
\text{AB}\Cdota\text{CD}+\text{BC}\Cdota\text{DA}=\text{AC}\Cdota\text{BD}
\end{align*}
が成り立つ。\text{AB}\Cdota\text{CD}+\text{BC}\Cdota\text{DA}=\text{AC}\Cdota\text{BD}
\end{align*}


ヒロ
「 対辺の積の和は対角線の積に等しい 」と覚えよう。

ヒロ
4点が円周上にないと使えないことにも注意しよう。
2011年 熊本大
2011年 熊本大四角形ABCDにおいて,
(1) $\cos A,~\cos B,~\cos C,~\cos D$ を $a,~b,~c,~d,~x,~y$ を用いて表せ。
(2) 四角形ABCDが円に内接するとき,$xy=ac+bd$ が成り立つことを示せ。
\begin{align*}
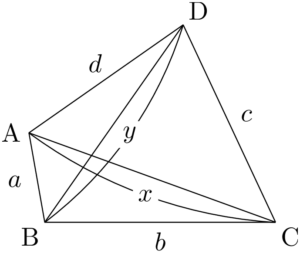
\text{AB}=a,~\text{BC}=b,~\text{CD}=c,~\text{DA}=d,~\text{AC}=x,~\text{BD}=y
\end{align*}
とする。以下の問いに答えよ。\text{AB}=a,~\text{BC}=b,~\text{CD}=c,~\text{DA}=d,~\text{AC}=x,~\text{BD}=y
\end{align*}
(1) $\cos A,~\cos B,~\cos C,~\cos D$ を $a,~b,~c,~d,~x,~y$ を用いて表せ。
(2) 四角形ABCDが円に内接するとき,$xy=ac+bd$ が成り立つことを示せ。
【(1)の考え方と解答】
適当な図を描くと次のようになる。
余弦定理より
適当な図を描くと次のようになる。

余弦定理より
\begin{align*}
&\cos A=\dfrac{a^2+d^2-y^2}{2ad},~\cos B=\dfrac{a^2+b^2-x^2}{2ab},\\[4pt]
&\cos C=\dfrac{b^2+c^2-y^2}{2bc},~\cos D=\dfrac{c^2+d^2-x^2}{2cd}
\end{align*}
&\cos A=\dfrac{a^2+d^2-y^2}{2ad},~\cos B=\dfrac{a^2+b^2-x^2}{2ab},\\[4pt]
&\cos C=\dfrac{b^2+c^2-y^2}{2bc},~\cos D=\dfrac{c^2+d^2-x^2}{2cd}
\end{align*}
(2) 四角形ABCDが円に内接するとき,$xy=ac+bd$ が成り立つことを示せ。
【(2)の考え方と解答】
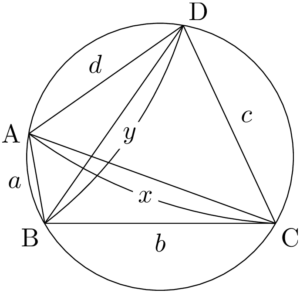
「四角形ABCDが円に内接する」という条件によって何が言えるのか,そしてそれを数式で表すとどうなるのかを考えよう。
「円に内接する四角形の性質」に「対角の和は180°」があるため,これを数式化すると $A+C=180\Deg$ となる。(1)でコサインを考えているから,$\cos A$ や $\cos C$ を考えると
それでは(1)の結果を利用して,$\cos A+\cos C=0$ を変形していこう。
同様に $\cos B+\cos D=0$ が成り立つから
①と②の辺々をかけて
「四角形ABCDが円に内接する」という条件によって何が言えるのか,そしてそれを数式で表すとどうなるのかを考えよう。

「円に内接する四角形の性質」に「対角の和は180°」があるため,これを数式化すると $A+C=180\Deg$ となる。(1)でコサインを考えているから,$\cos A$ や $\cos C$ を考えると
\begin{align*}
\cos C&=\cos(180\Deg-A) \\[4pt]
&=-\cos A
\end{align*}
となるから,$A+C=180\Deg$ が成り立つとき\cos C&=\cos(180\Deg-A) \\[4pt]
&=-\cos A
\end{align*}
\begin{align*}
\cos A+\cos C=0
\end{align*}
が成り立つことが分かる。このように「2段階」の変形が必要な問題をスムーズに解けるようになると,解ける問題数が一気に多くなる。「AならばB」という1段階変形で解ける問題については多くの人が苦労せずに解けるが,「AならばBであるから,さらにCとなる」のように2段階の変形が必要な問題になると,解ける人数が激減する。与えられた条件から何が言えるかをしっかり考えるようにしよう。小問に分かれている場合は,前の問題がヒントになっていることもあるから,そのヒントを逃さないようにしよう。\cos A+\cos C=0
\end{align*}
それでは(1)の結果を利用して,$\cos A+\cos C=0$ を変形していこう。
\begin{align*}
&\dfrac{a^2+d^2-y^2}{2ad}+\dfrac{b^2+c^2-y^2}{2bc}=0 \\[4pt]
&bc(a^2+d^2-y^2)+ad(b^2+c^2-y^2)=0 \\[4pt]
&(ad+bc)y^2=a^2bc+bcd^2+ab^2d+ac^2d \\[4pt]
&(ad+bc)y^2=bca^2+(b^2+c^2)da+bcd^2 \\[4pt]
&(ad+bc)y^2=(ba+cd)(ca+bd) \\[4pt]
&(ad+bc)y^2=(ab+cd)(ac+bd)~\cdots\cdots①
\end{align*}
得られた等式に $x$ が含まれていないから,もう1組の対角 $B,~D$ に着目する必要があることに気付く。&\dfrac{a^2+d^2-y^2}{2ad}+\dfrac{b^2+c^2-y^2}{2bc}=0 \\[4pt]
&bc(a^2+d^2-y^2)+ad(b^2+c^2-y^2)=0 \\[4pt]
&(ad+bc)y^2=a^2bc+bcd^2+ab^2d+ac^2d \\[4pt]
&(ad+bc)y^2=bca^2+(b^2+c^2)da+bcd^2 \\[4pt]
&(ad+bc)y^2=(ba+cd)(ca+bd) \\[4pt]
&(ad+bc)y^2=(ab+cd)(ac+bd)~\cdots\cdots①
\end{align*}
同様に $\cos B+\cos D=0$ が成り立つから
\begin{align*}
&\dfrac{a^2+b^2-x^2}{2ab}+\dfrac{c^2+d^2-x^2}{2cd}=0 \\[4pt]
&cd(a^2+b^2-x^2)+ab(c^2+d^2-x^2)=0 \\[4pt]
&(ab+cd)x^2=cda^2+(c^2+d^2)ba+b^2cd \\[4pt]
&(ab+cd)x^2=(ca+bd)(da+bc) \\[4pt]
&(ab+cd)x^2=(ad+bc)(ac+bd)~\cdots\cdots②
\end{align*}
証明するべき等式と①,②の形から辺々を掛ければ「$xy$」を含む式になることが分かるから辺々を掛けてみる。&\dfrac{a^2+b^2-x^2}{2ab}+\dfrac{c^2+d^2-x^2}{2cd}=0 \\[4pt]
&cd(a^2+b^2-x^2)+ab(c^2+d^2-x^2)=0 \\[4pt]
&(ab+cd)x^2=cda^2+(c^2+d^2)ba+b^2cd \\[4pt]
&(ab+cd)x^2=(ca+bd)(da+bc) \\[4pt]
&(ab+cd)x^2=(ad+bc)(ac+bd)~\cdots\cdots②
\end{align*}
①と②の辺々をかけて
\begin{align*}
&(ab+cd)(ad+bc)x^2y^2=(ab+cd)(ad+bc)(ac+bd)^2
\end{align*}
$ab+cd\neq0,~ad+bc\neq0$ であるから&(ab+cd)(ad+bc)x^2y^2=(ab+cd)(ad+bc)(ac+bd)^2
\end{align*}
\begin{align*}
x^2y^2=(ac+bd)^2
\end{align*}
$xy>0,~ac+bd>0$ であるからx^2y^2=(ac+bd)^2
\end{align*}
\begin{align*}
xy=ac+bd
\end{align*}
xy=ac+bd
\end{align*}
2018年 大妻女子大

ヒロ
中学校で学ぶ知識だけで解ける入試問題として,トレミーの定理の証明が出題されている。
2018年 大妻女子大次の問いの $\myhako$ に,解答群から正しいものを選び,それらの記号をマークせよ。同じものを何度選んでもよい。
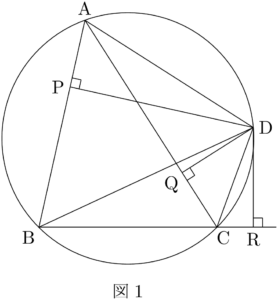
円に内接する四角形ABCDの頂点Dから直線AB,AC,BCに下ろした垂線を,それぞれDP,DQ,DRとする(図1参照)。ここで,点Pは線分ABを内分する点,点Qは線分ACを内分する点,点Rは線分BCを外分する点になる場合を考える。このとき,$\sankaku{DAP}$ と $\sankaku{DCR}$ の辺に対して,
解答群
ア $\text{AD}\Cdot\text{BR}$ イ $\text{AD}\Cdot\text{CR}$
ウ $\text{AD}\Cdot\text{DR}$ エ $\text{AP}\Cdot\text{BR}$
オ $\text{AP}\Cdot\text{CR}$ カ $\text{AP}\Cdot\text{DR}$
キ $\text{AQ}\Cdot\text{BC}$ ク $\text{AQ}\Cdot\text{CD}$
ケ $\text{BC}\Cdot\text{CQ}$ コ $\text{BC}\Cdot\text{CR}$
サ $\text{BD}\Cdot\text{CD}$ シ $\text{BD}\Cdot\text{DQ}$
ス $\text{BP}\Cdot\text{CD}$ セ $\text{BP}\Cdot\text{CQ}$
ソ $\text{BP}\Cdot\text{DQ}$ タ $\text{BP}\Cdot\text{DR}$
チ $\text{CQ}\Cdot\text{CR}$ ツ $\text{AP}+\text{BP}$
テ $\text{AP}-\text{BP}$ ト $\text{AQ}+\text{CQ}$
ナ $\text{AQ}-\text{CQ}$ ニ $\text{BR}+\text{CR}$
ヌ $\text{BR}-\text{CR}$
円に内接する四角形ABCDの頂点Dから直線AB,AC,BCに下ろした垂線を,それぞれDP,DQ,DRとする(図1参照)。ここで,点Pは線分ABを内分する点,点Qは線分ACを内分する点,点Rは線分BCを外分する点になる場合を考える。このとき,$\sankaku{DAP}$ と $\sankaku{DCR}$ の辺に対して,
\begin{align*}
\text{AP}\Cdota\text{CD}=\myBox{1}
\end{align*}
が成立する。すなわち\text{AP}\Cdota\text{CD}=\myBox{1}
\end{align*}
\begin{align*}
\text{AP}\Cdota\text{CD}-\mybox{1}=0~\cdots\cdots①
\end{align*}
また,$\sankaku{DAQ}$ と $\sankaku{DBR}$ の辺に対して,\text{AP}\Cdota\text{CD}-\mybox{1}=0~\cdots\cdots①
\end{align*}
\begin{align*}
\text{AQ}\Cdota\text{BD}=\myBox{2}~\cdots\cdots②
\end{align*}
$\sankaku{DPB}$ と $\sankaku{DQC}$ の辺に対して,\text{AQ}\Cdota\text{BD}=\myBox{2}~\cdots\cdots②
\end{align*}
\begin{align*}
\text{CQ}\Cdota\text{BD}=\myBox{2}~\cdots\cdots③
\end{align*}
が成り立つ。一方,$\text{AQ}+\text{CQ}=\text{AC}$ から\text{CQ}\Cdota\text{BD}=\myBox{2}~\cdots\cdots③
\end{align*}
\begin{align*}
\text{AQ}\Cdota\text{BD}+\text{CQ}\Cdota\text{BD}=\text{AC}\Cdota\text{BD}
\end{align*}
であり,②,③を用いると次式が得られる。\text{AQ}\Cdota\text{BD}+\text{CQ}\Cdota\text{BD}=\text{AC}\Cdota\text{BD}
\end{align*}
\begin{align*}
\text{BR}\Cdota\text{AD}+\myBox{3}=\text{AC}\Cdota\text{BD}~\cdots\cdots④
\end{align*}
となる。このことから,円に内接する四角形ABCDの4つの辺と2つの対角線との間に\text{BR}\Cdota\text{AD}+\myBox{3}=\text{AC}\Cdota\text{BD}~\cdots\cdots④
\end{align*}
\begin{align*}
\text{BC}\Cdota\text{AD}+\text{AB}\Cdota\text{CD}=\text{AC}\Cdota\text{BD}
\end{align*}
となる関係が存在することが分かる。\text{BC}\Cdota\text{AD}+\text{AB}\Cdota\text{CD}=\text{AC}\Cdota\text{BD}
\end{align*}

解答群
ア $\text{AD}\Cdot\text{BR}$ イ $\text{AD}\Cdot\text{CR}$
ウ $\text{AD}\Cdot\text{DR}$ エ $\text{AP}\Cdot\text{BR}$
オ $\text{AP}\Cdot\text{CR}$ カ $\text{AP}\Cdot\text{DR}$
キ $\text{AQ}\Cdot\text{BC}$ ク $\text{AQ}\Cdot\text{CD}$
ケ $\text{BC}\Cdot\text{CQ}$ コ $\text{BC}\Cdot\text{CR}$
サ $\text{BD}\Cdot\text{CD}$ シ $\text{BD}\Cdot\text{DQ}$
ス $\text{BP}\Cdot\text{CD}$ セ $\text{BP}\Cdot\text{CQ}$
ソ $\text{BP}\Cdot\text{DQ}$ タ $\text{BP}\Cdot\text{DR}$
チ $\text{CQ}\Cdot\text{CR}$ ツ $\text{AP}+\text{BP}$
テ $\text{AP}-\text{BP}$ ト $\text{AQ}+\text{CQ}$
ナ $\text{AQ}-\text{CQ}$ ニ $\text{BR}+\text{CR}$
ヌ $\text{BR}-\text{CR}$
【考え方と解答】
$\text{AP}\Cdot\text{CD}$ を求めるから,APとCDを含む2つの三角形を考える。その2つの三角形が相似なら,さらに都合が良い。したがって,$\sankaku{DAP}$ と $\sankaku{DCR}$ に着目する。
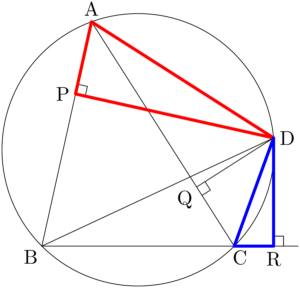
四角形ABCDが円に内接する四角形であるから,$\kaku{PAD}=\kaku{DCR}$ である。2つの三角形は直角三角形であるから,2つの内角がそれぞれ等しいから相似である。
よって
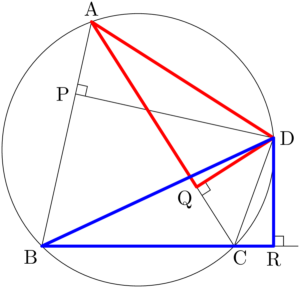
$\sankaku{DAQ}$ と $\sankaku{DBR}$ において,$\ko{\text{CD}}$ に対する円周角に着目すると
したがって
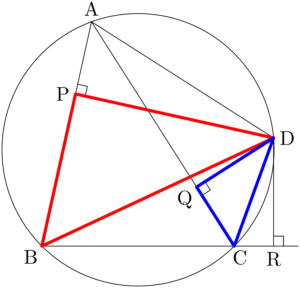
$\ko{\text{AD}}$ に対する円周角より
よって
$\text{AP}\Cdot\text{CD}$ を求めるから,APとCDを含む2つの三角形を考える。その2つの三角形が相似なら,さらに都合が良い。したがって,$\sankaku{DAP}$ と $\sankaku{DCR}$ に着目する。

四角形ABCDが円に内接する四角形であるから,$\kaku{PAD}=\kaku{DCR}$ である。2つの三角形は直角三角形であるから,2つの内角がそれぞれ等しいから相似である。
よって
\begin{align*}
&\text{AP}:\text{CR}=\text{AD}:\text{CD} \\[4pt]
&\text{AP}\Cdota\text{CD}=\text{AD}\Cdota\text{CR}(イ) \\[4pt]
&\text{AP}\Cdota\text{CD}-\text{AD}\Cdota\text{CR}=0~\cdots\cdots①
\end{align*}
&\text{AP}:\text{CR}=\text{AD}:\text{CD} \\[4pt]
&\text{AP}\Cdota\text{CD}=\text{AD}\Cdota\text{CR}(イ) \\[4pt]
&\text{AP}\Cdota\text{CD}-\text{AD}\Cdota\text{CR}=0~\cdots\cdots①
\end{align*}

$\sankaku{DAQ}$ と $\sankaku{DBR}$ において,$\ko{\text{CD}}$ に対する円周角に着目すると
\begin{align*}
\kaku{DAQ}=\kaku{DBR}
\end{align*}
であり,2つの三角形は直角三角形であるから $\sankaku{DAQ}$∽$\sankaku{DBR}$ である。\kaku{DAQ}=\kaku{DBR}
\end{align*}
したがって
\begin{align*}
&\text{AQ}:\text{BR}=\text{AD}:\text{BD} \\[4pt]
&\text{AQ}\Cdota\text{BD}=\text{AD}\Cdota\text{BR}(ア)~\cdots\cdots②
\end{align*}
次は $\sankaku{DPB}$ と $\sankaku{DQC}$ に着目する。&\text{AQ}:\text{BR}=\text{AD}:\text{BD} \\[4pt]
&\text{AQ}\Cdota\text{BD}=\text{AD}\Cdota\text{BR}(ア)~\cdots\cdots②
\end{align*}

$\ko{\text{AD}}$ に対する円周角より
\begin{align*}
\kaku{PBQ}=\kaku{QCD}
\end{align*}
であり,2つの三角形は直角三角形であるから $\sankaku{DPB}$∽$\sankaku{DQC}$ である。\kaku{PBQ}=\kaku{QCD}
\end{align*}
よって
\begin{align*}
&\text{BP}:\text{CQ}=\text{BD}:\text{CD} \\[4pt]
&\text{CQ}\Cdota\text{BD}=\text{BP}\Cdota\text{CD}(ス)~\cdots\cdots③
\end{align*}
一方,$\text{AQ}+\text{CQ}=\text{AC}$ の両辺にBDをかけると&\text{BP}:\text{CQ}=\text{BD}:\text{CD} \\[4pt]
&\text{CQ}\Cdota\text{BD}=\text{BP}\Cdota\text{CD}(ス)~\cdots\cdots③
\end{align*}
\begin{align*}
\text{AQ}\Cdota\text{BD}+\text{CQ}\Cdota\text{BD}=\text{AC}\Cdota\text{BD}
\end{align*}
となり,②,③を用いると次のようになる。\text{AQ}\Cdota\text{BD}+\text{CQ}\Cdota\text{BD}=\text{AC}\Cdota\text{BD}
\end{align*}
\begin{align*}
&\text{AD}\Cdota\text{BR}+\text{BP}\Cdota\text{CD}=\text{AC}\Cdota\text{BD}(ス)~\cdots\cdots④
\end{align*}
$①+④$ より&\text{AD}\Cdota\text{BR}+\text{BP}\Cdota\text{CD}=\text{AC}\Cdota\text{BD}(ス)~\cdots\cdots④
\end{align*}
\begin{align*}
&\text{AD}\Cdota(\text{BR}-\text{CR})+\text{CD}\Cdota(\text{AP}+\text{BP})=\text{AC}\Cdota\text{BD}(ヌ,ツ) \\[4pt]
&\text{AD}\Cdota\text{BC}+\text{AB}\Cdota\text{CD}=\text{AC}\Cdota\text{BD}
\end{align*}
&\text{AD}\Cdota(\text{BR}-\text{CR})+\text{CD}\Cdota(\text{AP}+\text{BP})=\text{AC}\Cdota\text{BD}(ヌ,ツ) \\[4pt]
&\text{AD}\Cdota\text{BC}+\text{AB}\Cdota\text{CD}=\text{AC}\Cdota\text{BD}
\end{align*}