係数に文字を含む3次方程式の実数解の位置や個数に関する問題の考え方と解法を説明します。
3次方程式の実数解の個数を数えるとき,その方程式を解こうとしても解けない場合もあります。そのような問題に対する考え方を身に付けましょう。
Contents
方程式の実数解の個数について

ヒロ
ある方程式の実数解の個数を求めたいとき,その方程式を解くことができるなら,解いてしまえば良い。

ヒロ
しかし,方程式を解くことが難しい場合は,別の方法を考えよう。

ヒロ
係数に文字を含む方程式のうち,定数項だけに文字が含まれているときは,その文字を分離して考える方法が良いだろう。
$f(x)=a$ の実数解$x$ についての方程式 $f(x)=a$($a$ は定数)の実数解の個数は,$y=f(x)$ のグラフと $y=a$ のグラフの共有点の個数に等しい。

ヒロ
この考え方は,3次方程式だけでなく,様々な方程式において有効である。$y=f(x)$ のグラフを描くことができれば,$x$ 軸と平行な直線 $y=a$ との共有点の個数を数えることで,$f(x)=a$ の実数解の個数を求めることができる。
2021年 広島修道大
2021年 広島修道大3次方程式 $x^3-3x+2-a=0$ について,次の問に答えよ。
(1) この3次方程式が異なる2つの負の解と1つの正の解をもつように,定数 $a$ の値の範囲を定めよ。
(2) この3次方程式が異なる3つの実数解をもつとき,この3つの解を小さい順に $\alpha,\beta,\gamma$ とする。このとき,$\alpha,\beta,\gamma$ の値の範囲をそれぞれ求めよ。
(1) この3次方程式が異なる2つの負の解と1つの正の解をもつように,定数 $a$ の値の範囲を定めよ。
(2) この3次方程式が異なる3つの実数解をもつとき,この3つの解を小さい順に $\alpha,\beta,\gamma$ とする。このとき,$\alpha,\beta,\gamma$ の値の範囲をそれぞれ求めよ。
【(1)の解答と考え方】
因数分解しようとしてもできないから,$a$ を分離して考える。
$x^3-3x+2-a=0~\cdots\cdots①$ より,$x^3-3x+2=a$
$f(x)=x^3-3x+2$ とおくと,①の実数解は $y=f(x)$ のグラフと $y=a$ のグラフの共有点の $x$ 座標である。
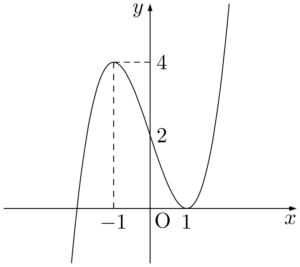
条件をみたすのは,$y=f(x)$ のグラフと $y=a$ のグラフの共有点が3個あり,そのうち2つは $x<0$ の部分にあり,残りの1つは $x>0$ の部分にあるときである。
したがって,求める $a$ の値の範囲は,$2<a<4$
因数分解しようとしてもできないから,$a$ を分離して考える。
$x^3-3x+2-a=0~\cdots\cdots①$ より,$x^3-3x+2=a$
$f(x)=x^3-3x+2$ とおくと,①の実数解は $y=f(x)$ のグラフと $y=a$ のグラフの共有点の $x$ 座標である。
\begin{align*}
f'(x)&=3x^2-3 \\[4pt]
&=3(x+1)(x-1)
\end{align*}
$f'(x)=0$ とすると,$x=\pm1$f'(x)&=3x^2-3 \\[4pt]
&=3(x+1)(x-1)
\end{align*}
\begin{align*}
\begin{array}{|c||c|c|c|c|c|}\hline
x & \cdots & -1 & \cdots & 1 & \cdots \\\hline
f'(x) & + & 0 & – & 0 & + \\\hline
f(x) & \nearrow & 極大 & \searrow & 極小 & \nearrow \\\hline
\end{array}
\end{align*}
よって,$y=f(x)$ のグラフは次のようになる。\begin{array}{|c||c|c|c|c|c|}\hline
x & \cdots & -1 & \cdots & 1 & \cdots \\\hline
f'(x) & + & 0 & – & 0 & + \\\hline
f(x) & \nearrow & 極大 & \searrow & 極小 & \nearrow \\\hline
\end{array}
\end{align*}

条件をみたすのは,$y=f(x)$ のグラフと $y=a$ のグラフの共有点が3個あり,そのうち2つは $x<0$ の部分にあり,残りの1つは $x>0$ の部分にあるときである。
したがって,求める $a$ の値の範囲は,$2<a<4$
(2) この3次方程式が異なる3つの実数解をもつとき,この3つの解を小さい順に $\alpha,\beta,\gamma$ とする。このとき,$\alpha,\beta,\gamma$ の値の範囲をそれぞれ求めよ。
【(2)の解答と考え方】
$f(x)=0$ を解くと
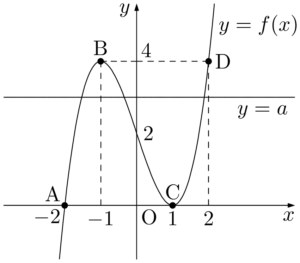
$y=f(x)$ のグラフと $y=a$ のグラフが異なる3点で交わるとき,その交点は $y=f(x)$ のグラフ上の点Aと点Bの間に1つ,点Bと点Cの間に1つ,点Cと点Dの間に1つある。したがって,
$f(x)=0$ を解くと
\begin{align*}
&x^3-3x+2=0 \\[4pt]
&(x-1)^2(x+2)=0 \\[4pt]
&x=1,~-2
\end{align*}
$f(x)=4$ を解くと&x^3-3x+2=0 \\[4pt]
&(x-1)^2(x+2)=0 \\[4pt]
&x=1,~-2
\end{align*}
\begin{align*}
&x^3-3x+2=4 \\[4pt]
&x^3-3x-2=0 \\[4pt]
&(x+1)^2(x-2)=0 \\[4pt]
&x=-1,~2
\end{align*}
&x^3-3x+2=4 \\[4pt]
&x^3-3x-2=0 \\[4pt]
&(x+1)^2(x-2)=0 \\[4pt]
&x=-1,~2
\end{align*}

$y=f(x)$ のグラフと $y=a$ のグラフが異なる3点で交わるとき,その交点は $y=f(x)$ のグラフ上の点Aと点Bの間に1つ,点Bと点Cの間に1つ,点Cと点Dの間に1つある。したがって,
\begin{align*}
-2<\alpha<-1,~-1<\beta<1,~1<\gamma<2
\end{align*}
-2<\alpha<-1,~-1<\beta<1,~1<\gamma<2
\end{align*}


















