ここではヘロンの公式について説明します。
ヘロンの公式は三角形の3辺の長さからその面積を求めることができる公式です。
三角形の3辺の長さが分かっているときは,次の記事でも説明しているように,三角比の値を利用して三角形の面積を求めることができます。
したがって,三角形の面積を求めるためにヘロンの公式を使うことはほとんどありません。
しかし,ヘロンの公式の証明をさせる問題が入試問題として出題されることもあるため,ヘロンの公式があることを知り,証明を一度は経験しておくことは重要です。
三角形の面積を求める入試問題【2003年 小樽商科大】

ヒロ
次の入試問題を解くことで,3辺の長さから三角形の面積を求めてみよう。
2003年 小樽商科大$\sankaku{ABC}$ の3つの角の大きさを $A,~B,~C$ で,それらの角の対辺の長さをそれぞれ $a,~b,~c$ で表すとき,以下の設問に答えよ。
(1) $\cos A$ を $a,~b,~c$ で,$\sankaku{ABC}$ の面積 $S$ を $A,~b,~c$ で表せ。
(2) $S^2$ を $a,~b,~c$ で表し,因数分解せよ。
(1) $\cos A$ を $a,~b,~c$ で,$\sankaku{ABC}$ の面積 $S$ を $A,~b,~c$ で表せ。
(2) $S^2$ を $a,~b,~c$ で表し,因数分解せよ。
【(1)の考え方と解答】
3辺の長さからコサインの値を求めれば良いから余弦定理を使えば良いね。
余弦定理より,
3辺の長さからコサインの値を求めれば良いから余弦定理を使えば良いね。
余弦定理より,
\begin{align*}
\cos A=\dfrac{b^2+c^2-a^2}{2bc}~\cdots\cdots①
\end{align*}
また,$\sankaku{ABC}$ の面積 $S$ は,\cos A=\dfrac{b^2+c^2-a^2}{2bc}~\cdots\cdots①
\end{align*}
\begin{align*}
S=\dfrac{1}{2}bc\sin A~\cdots\cdots②
\end{align*}
S=\dfrac{1}{2}bc\sin A~\cdots\cdots②
\end{align*}
(2) $S^2$ を $a,~b,~c$ で表し,因数分解せよ。
【(2)の考え方と解答】
①と②から $A$ を消去しよう。
①より
①と②から $A$ を消去しよう。
①より
\begin{align*}
\sin^2A&=1-\cos^2A \\[4pt]
&=1-\left(\dfrac{b^2+c^2-a^2}{2bc}\right)^2 \\[4pt]
&=\dfrac{(2bc)^2-(b^2+c^2-a^2)^2}{4b^2c^2} \\[4pt]
&=\dfrac{(2bc+b^2+c^2-a^2)(2bc-b^2-c^2+a^2)}{4b^2c^2} \\[4pt]
&=\dfrac{\{(b+c)^2-a^2\}\{a^2-(b-c)^2\}}{4b^2c^2} \\[4pt]
&=\dfrac{(b+c+a)(b+c-a)(a+b-c)(a-b+c)}{4b^2c^2}
\end{align*}
よって,②より\sin^2A&=1-\cos^2A \\[4pt]
&=1-\left(\dfrac{b^2+c^2-a^2}{2bc}\right)^2 \\[4pt]
&=\dfrac{(2bc)^2-(b^2+c^2-a^2)^2}{4b^2c^2} \\[4pt]
&=\dfrac{(2bc+b^2+c^2-a^2)(2bc-b^2-c^2+a^2)}{4b^2c^2} \\[4pt]
&=\dfrac{\{(b+c)^2-a^2\}\{a^2-(b-c)^2\}}{4b^2c^2} \\[4pt]
&=\dfrac{(b+c+a)(b+c-a)(a+b-c)(a-b+c)}{4b^2c^2}
\end{align*}
\begin{align*}
S^2&=\dfrac{1}{4}b^2c^2\sin^2A \\[4pt]
&=\dfrac{1}{4}b^2c^2\Cdota\dfrac{(b+c+a)(b+c-a)(a+b-c)(a-b+c)}{4b^2c^2} \\[4pt]
&=\dfrac{1}{16}(b+c+a)(b+c-a)(a+b-c)(a-b+c)
\end{align*}
S^2&=\dfrac{1}{4}b^2c^2\sin^2A \\[4pt]
&=\dfrac{1}{4}b^2c^2\Cdota\dfrac{(b+c+a)(b+c-a)(a+b-c)(a-b+c)}{4b^2c^2} \\[4pt]
&=\dfrac{1}{16}(b+c+a)(b+c-a)(a+b-c)(a-b+c)
\end{align*}
三角形の面積を求める公式【ヘロンの公式】

ヒロ
上の2003年小樽商科大の入試問題の結果がヘロンの公式であるが,よく見る形にしておこう。
【ヘロンの公式】
三角形の3辺の長さが $a,~b,~c$ のとき,その三角形の面積を $S$ とすると
三角形の3辺の長さが $a,~b,~c$ のとき,その三角形の面積を $S$ とすると
\begin{align*}
S^2&=\dfrac{1}{16}(b+c+a)(b+c-a)(a+b-c)(a-b+c)
\end{align*}
ここで $\dfrac{a+b+c}{2}=s$ とおくとS^2&=\dfrac{1}{16}(b+c+a)(b+c-a)(a+b-c)(a-b+c)
\end{align*}
\begin{align*}
&\dfrac{b+c-a}{2}=\dfrac{a+b+c}{2}-a=s-a \\[4pt]
&\dfrac{a+b-c}{2}=\dfrac{a+b+c}{2}-c=s-c \\[4pt]
&\dfrac{a-b+c}{2}=\dfrac{a+b+c}{2}-b=s-b \\[4pt]
\end{align*}
であるから&\dfrac{b+c-a}{2}=\dfrac{a+b+c}{2}-a=s-a \\[4pt]
&\dfrac{a+b-c}{2}=\dfrac{a+b+c}{2}-c=s-c \\[4pt]
&\dfrac{a-b+c}{2}=\dfrac{a+b+c}{2}-b=s-b \\[4pt]
\end{align*}
\begin{align*}
&S^2=s(s-a)(s-b)(s-c) \\[4pt]
&S=\sqrt{s(s-a)(s-b)(s-c)}
\end{align*}
&S^2=s(s-a)(s-b)(s-c) \\[4pt]
&S=\sqrt{s(s-a)(s-b)(s-c)}
\end{align*}

ヒロ
個人的には,面積を大文字の $S$ で表すのに,その公式の中で小文字の $s$ を使うのは辞めて欲しい。
ヘロンの公式三角形の3辺の長さを $a,~b,~c$ とし,$s=\dfrac{a+b+c}{2}$ とおくと,三角形の面積 $S$ は
\begin{align*}
S=\sqrt{s(s-a)(s-b)(s-c)}
\end{align*}
と表される。S=\sqrt{s(s-a)(s-b)(s-c)}
\end{align*}
ヘロンの公式を使う練習

ヒロ
ヘロンの公式を利用することで,楽かどうかはおいといて,3辺の長さから面積を求めることができるようになる。
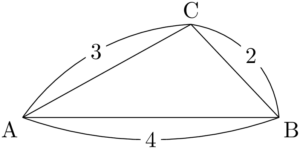
問題$\sankaku{ABC}$ において,$a=4,~b=3,~c=2$ のとき,この三角形の面積 $S$ を求めよ。
【考え方と解答】
今回はヘロンの公式を用いて面積を求めよう。
$s=\dfrac{4+3+2}{2}=\dfrac{9}{2}$ とおくと,ヘロンの公式より
今回はヘロンの公式を用いて面積を求めよう。

$s=\dfrac{4+3+2}{2}=\dfrac{9}{2}$ とおくと,ヘロンの公式より
\begin{align*}
S&=\sqrt{s(s-a)(s-b)(s-c)} \\[4pt]
&=\sqrt{\dfrac{9}{2}\left(\dfrac{9}{2}-4\right)\left(\dfrac{9}{2}-3\right)\left(\dfrac{9}{2}-2\right)} \\[4pt]
&=\sqrt{\dfrac{9}{2}\Cdot\dfrac{1}{2}\Cdot\dfrac{3}{2}\Cdot\dfrac{5}{2}} \\[4pt]
&=\dfrac{3\sqrt{15}}{4}
\end{align*}
S&=\sqrt{s(s-a)(s-b)(s-c)} \\[4pt]
&=\sqrt{\dfrac{9}{2}\left(\dfrac{9}{2}-4\right)\left(\dfrac{9}{2}-3\right)\left(\dfrac{9}{2}-2\right)} \\[4pt]
&=\sqrt{\dfrac{9}{2}\Cdot\dfrac{1}{2}\Cdot\dfrac{3}{2}\Cdot\dfrac{5}{2}} \\[4pt]
&=\dfrac{3\sqrt{15}}{4}
\end{align*}


















