ここでは2つの円の交点を通る円について説明します。
円と直線の交点を通る直線や円の方程式を求める方法を理解していれば,この記事に書かれている内容も簡単に理解できるでしょう。
Contents
2つの円の交点を通る円

ヒロ
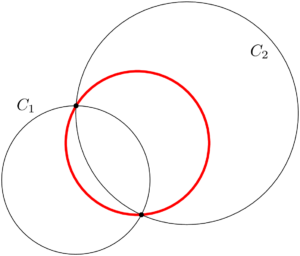
2つの円の共有点を通る円の方程式の公式を書くと次のようになる。
2つの円の共有点を通る円2つの円
また,$k_1$ と $k_2$ のどちらを残すかは自由なので
\begin{align*}
&x^2+y^2+lx+my+n=0~\cdots\cdots① \\[4pt]
&x^2+y^2+px+qy+r=0~\cdots\cdots②
\end{align*}
が共有点をもつとき,その共有点をすべて通る円の方程式は&x^2+y^2+lx+my+n=0~\cdots\cdots① \\[4pt]
&x^2+y^2+px+qy+r=0~\cdots\cdots②
\end{align*}
\begin{align*}
k_1(x^2+y^2+lx+my+n)+k_2(x^2+y^2+px+qy+r)=0~\cdots\cdots③
\end{align*}
と表される。$k_1=0$ のときは③は②と一致し,$k_2=0$ のときは③は①と一致する。どちらか一方と一致しなくても良い場合は,①と②の共有点を通る円の方程式をk_1(x^2+y^2+lx+my+n)+k_2(x^2+y^2+px+qy+r)=0~\cdots\cdots③
\end{align*}
\begin{align*}
k(x^2+y^2+lx+my+n)+(x^2+y^2+px+qy+r)=0
\end{align*}
とおいても良い。1文字しか使っていないため,$k_1$を$k$に書き換えた。k(x^2+y^2+lx+my+n)+(x^2+y^2+px+qy+r)=0
\end{align*}
また,$k_1$ と $k_2$ のどちらを残すかは自由なので
\begin{align*}
(x^2+y^2+lx+my+n)+k(x^2+y^2+px+qy+r)=0
\end{align*}
とおいても良い。先ほど同様,$k_2$を$k$に書き換えた。(x^2+y^2+lx+my+n)+k(x^2+y^2+px+qy+r)=0
\end{align*}


ヒロ
2つの円の交点を通る直線を利用する方法も考えられる。
2つの円の共有点を通る円Ⅱ2つの円
\begin{align*}
&x^2+y^2+lx+my+n=0~\cdots\cdots① \\[4pt]
&x^2+y^2+px+qy+r=0~\cdots\cdots②
\end{align*}
が共有点をもつとき,その共有点をすべて通る直線の方程式は,$①-②$ を計算することで得られて&x^2+y^2+lx+my+n=0~\cdots\cdots① \\[4pt]
&x^2+y^2+px+qy+r=0~\cdots\cdots②
\end{align*}
\begin{align*}
(l-p)x+(m-q)y+n-r=0~\cdots\cdots③
\end{align*}
となる。「①かつ②」は「①かつ③」であるから,2つの円の共有点を通る円は,円①と直線③の共有点を通る円でもあるから(l-p)x+(m-q)y+n-r=0~\cdots\cdots③
\end{align*}
\begin{align*}
k_1(x^2+y^2+lx+my+n)+k_2\{(l-p)x+(m-q)y+n-r\}=0~\cdots\cdots④
\end{align*}
と表される。$k_1=0$ のときは④は③と一致し,$k_2=0$ のときは④は①と一致する。どちらか一方と一致しなくても良い場合は,残す方の係数を$k$として,①と②の共有点を通る円の方程式をk_1(x^2+y^2+lx+my+n)+k_2\{(l-p)x+(m-q)y+n-r\}=0~\cdots\cdots④
\end{align*}
\begin{align*}
k(x^2+y^2+lx+my+n)+(l-p)x+(m-q)y+n-r=0
\end{align*}
とおいても良い。$k_2$ を残す場合はk(x^2+y^2+lx+my+n)+(l-p)x+(m-q)y+n-r=0
\end{align*}
\begin{align*}
(x^2+y^2+lx+my+n)+k\{(l-p)x+(m-q)y+n-r\}=0
\end{align*}
とおけば良い。(x^2+y^2+lx+my+n)+k\{(l-p)x+(m-q)y+n-r\}=0
\end{align*}


















