【数学ⅡB】三角形の重心の座標【関西学院大】

Contents

ページ1
1 三角形の重心
ページ2
1 三角形の重心の性質
2 三角形の重心の座標
3 三角形の重心の座標を求める問題

三角形の重心の性質

ヒロ

次に三角形の重心の性質を知ろう。

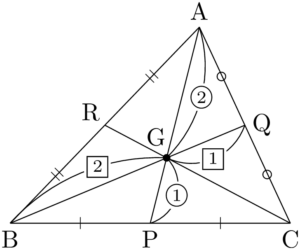
三角形の重心の性質三角形の重心は中線を $2:1$ の比に内分する。つまり，3辺AB，BC，CAの中点をそれぞれP，Q，Rとすると

\begin{align*}
&\text{AG}:\text{GP}=2:1 \\[4pt]
&\text{BG}:\text{GQ}=2:1 \\[4pt]
&\text{CG}:\text{GR}=2:1
\end{align*}

が成り立つ。

三角形の重心の座標

ヒロ

次に三角形の重心の座標を求める。

【三角形の重心の座標】
　平面上の3点A$(x_1,~y_1)$，B$(x_2,~y_2)$，C$(x_3,~y_3)$ に対して，$\sankaku{ABC}$ の重心をG$(x,~y)$ とする。BCの中点をM$(p,~q)$ とすると，重心Gは線分AMを $2:1$ に内分する点である。

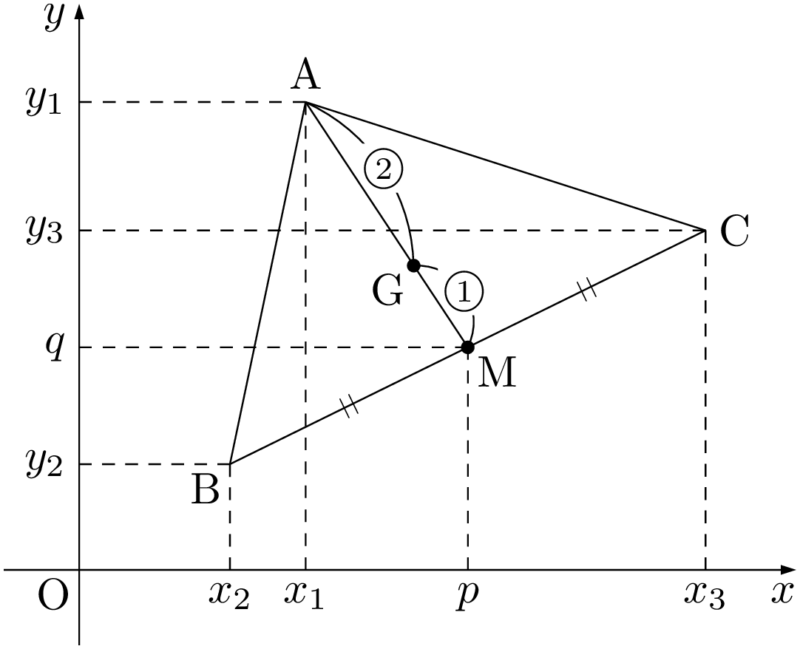
重心Gの座標は

\begin{align*}
x=\dfrac{2p+x_1}{3},~y=\dfrac{2q+y_1}{3}
\end{align*}

であり，M$(p,~q)$ の座標は

\begin{align*}
p=\dfrac{x_2+x_3}{2},~q=\dfrac{y_2+y_3}{2}
\end{align*}

であるから，

\begin{align*}
x&=\dfrac{2}{3}\Cdota\dfrac{x_2+x_3}{2}+\dfrac{1}{3}x_1 \\[4pt]
&=\dfrac{x_1+x_2+x_3}{3} \\[4pt]
y&=\dfrac{2}{3}\Cdota\dfrac{y_2+y_3}{2}+\dfrac{1}{3}y_1 \\[4pt]
&=\dfrac{y_1+y_2+y_3}{3}
\end{align*}

したがって，重心Gの座標は $\left(\dfrac{x_1+x_2+x_3}{3},~\dfrac{y_1+y_2+y_3}{3}\right)$

ヒロ

三角形の重心の座標は「三角形の頂点の座標をすべて加えて3で割ったもの」であるから簡単に覚えられるだろう。

三角形の重心の座標平面上の3点A$(x_1,~y_1)$，B$(x_2,~y_2)$，C$(x_3,~y_3)$ に対して，$\sankaku{ABC}$ の重心Gの座標は G$\left(\dfrac{x_1+x_2+x_3}{3},~\dfrac{y_1+y_2+y_3}{3}\right)$ である。

三角形の重心の座標を求める問題

2018年関西学院大座標平面上に3点A$(-2,~3)$，B$(4,~-1)$，P$(3p-3,~-p+6)$ がある。$\sankaku{ABP}$ の重心が直線 $y=2x$ 上にあるとすると，$p=\myhako$ である。

【考え方と解答】
まずは重心の座標を求めよう。$\sankaku{ABP}$ の重心をG$(x,~y)$ とすると

\begin{align*}
&x=\dfrac{-2+4+(3p-3)}{3}=\dfrac{3p-1}{3} \\[4pt]
&y=\dfrac{3+(-1)+(-p+6)}{3}=\dfrac{-p+8}{3}
\end{align*}

よって，G$\left(\dfrac{3p-1}{3},~\dfrac{-p+8}{3}\right)$ となり，この点が直線 $y=2x$ 上にあるときを考えて

\begin{align*}
&\dfrac{-p+8}{3}=2\Cdota\dfrac{3p-1}{3} \\[4pt]
&-p+8=2(3p-1) \\[4pt]
&p=\dfrac{10}{7}
\end{align*}