3次関数のグラフと面積について説明します。
3次関数のグラフと面積の問題についても,2次関数の場合と基本は変わりません。
積分区間とグラフの上下関係に注意して,丁寧に定積分の計算をして面積を求めましょう。
定積分の問題で間違えた場合は,積分そのものが間違っているか,数値計算が間違っているか分からなくなるため,積分自体を間違えないようにすることが重要です。
Contents
2020年 明治大
2020年 明治大実数 $a>0$ について,関数 $f(x)=2x^3-3(a-1)x^2-6ax$ が,極小値 $-4$ をとるとき,$a=\myhako$ であり,曲線 $y=f(x)$ と $x$ 軸で囲まれた図形の面積は,$\myhako$ である。
【解答と考え方】
極小値をとる $x$ の値を求めるために微分しよう。
このとき $f(x)=2x^3-6x$ となる。$y=0$ とすると
原点に関して点対称であるから,求める面積を $S$ とすると
極小値をとる $x$ の値を求めるために微分しよう。
\begin{align*}
f'(x)&=6x^2-6(a-1)x-6a \\[4pt]
&=6(x-a)(x+1)
\end{align*}
$a>0>-1$ であるから,$f(x)$ の増減は次のようになる。f'(x)&=6x^2-6(a-1)x-6a \\[4pt]
&=6(x-a)(x+1)
\end{align*}
\begin{align*}
\begin{array}{|c||c|c|c|c|c|}\hline
x & \cdots & -1 & \cdots & a & \cdots \\\hline
f'(x) & + & 0 & – & 0 & + \\\hline
f(x) & \nearrow & 極大 & \searrow & 極小 & \nearrow \\\hline
\end{array}
\end{align*}
したがって,$f(x)$ は $x=a$ で極小となる。極小値が $-4$ のとき,$f(a)=-4$ が成り立つから\begin{array}{|c||c|c|c|c|c|}\hline
x & \cdots & -1 & \cdots & a & \cdots \\\hline
f'(x) & + & 0 & – & 0 & + \\\hline
f(x) & \nearrow & 極大 & \searrow & 極小 & \nearrow \\\hline
\end{array}
\end{align*}
\begin{align*}
&2a^3-3(a-1)a^2-6a^2=-4 \\[4pt]
&a^3+3a^2-4=0 \\[4pt]
&(a-1)(a^2+4a+4)=0 \\[4pt]
&(a-1)(a+2)^2=0 \\[4pt]
&a=1,~-2
\end{align*}
$a>0$ より,$a=1$&2a^3-3(a-1)a^2-6a^2=-4 \\[4pt]
&a^3+3a^2-4=0 \\[4pt]
&(a-1)(a^2+4a+4)=0 \\[4pt]
&(a-1)(a+2)^2=0 \\[4pt]
&a=1,~-2
\end{align*}
このとき $f(x)=2x^3-6x$ となる。$y=0$ とすると
\begin{align*}
&2x^3-6x=0 \\[4pt]
&2x(x^2-3)=0 \\[4pt]
&x=0,~\pm\sqrt{3}
\end{align*}
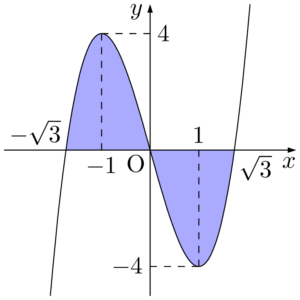
よって,$y=f(x)$ のグラフと $x$ 軸で囲まれた図形は次の図の色を塗った部分となる。&2x^3-6x=0 \\[4pt]
&2x(x^2-3)=0 \\[4pt]
&x=0,~\pm\sqrt{3}
\end{align*}

原点に関して点対称であるから,求める面積を $S$ とすると
\begin{align*}
S&=2\dint{-\sqrt{3}}{0}(2x^3-6x)\;dx \\[4pt]
&=2\Tint{\dfrac{1}{2}x^4-3x^2}{-\sqrt{3}}{0} \\[4pt]
&=-2\left(\dfrac{9}{2}-9\right) \\[4pt]
&=9
\end{align*}
S&=2\dint{-\sqrt{3}}{0}(2x^3-6x)\;dx \\[4pt]
&=2\Tint{\dfrac{1}{2}x^4-3x^2}{-\sqrt{3}}{0} \\[4pt]
&=-2\left(\dfrac{9}{2}-9\right) \\[4pt]
&=9
\end{align*}
2021年 東京女子大
2021年 東京女子大$f(x)=x^3+x^2-x+2$,$g(x)=2x^2+3x-2$ とするとき,以下の設問に答えよ。
(1) $f(x)\geqq g(x)$ となるような $x$ の範囲を求めよ。
(2) $y=f(x)$ と $y=g(x)$ のグラフで囲まれた2つの部分の面積の和を求めよ。
(1) $f(x)\geqq g(x)$ となるような $x$ の範囲を求めよ。
(2) $y=f(x)$ と $y=g(x)$ のグラフで囲まれた2つの部分の面積の和を求めよ。
【(1)の解答と考え方】
$f(x)\geqq g(x)$ より
$f(x)\geqq g(x)$ より
\begin{align*}
&(x^3+x^2-x+2)-(2x^2+3x-2)\geqq0 \\[4pt]
&x^3-x^2-4x+4\geqq0 \\[4pt]
&(x-1)(x^2-4)\geqq0 \\[4pt]
&(x-1)(x+2)(x-2)\geqq0 \\[4pt]
&-2\leqq x\leqq1,~2\leqq x
\end{align*}
&(x^3+x^2-x+2)-(2x^2+3x-2)\geqq0 \\[4pt]
&x^3-x^2-4x+4\geqq0 \\[4pt]
&(x-1)(x^2-4)\geqq0 \\[4pt]
&(x-1)(x+2)(x-2)\geqq0 \\[4pt]
&-2\leqq x\leqq1,~2\leqq x
\end{align*}

(2) $y=f(x)$ と $y=g(x)$ のグラフで囲まれた2つの部分の面積の和を求めよ。
【(2)の解答と考え方】
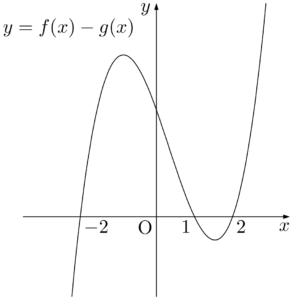
求める面積を $S$ とすると,$S$ は曲線 $y=f(x)-g(x)$ と $x$ 軸で囲まれた部分の面積に等しい。
求める面積を $S$ とすると,$S$ は曲線 $y=f(x)-g(x)$ と $x$ 軸で囲まれた部分の面積に等しい。
\begin{align*}
\dint{}{}(f(x)-g(x))\;dx&=\dint{}{}(x^3-x^2-4x+4)\;dx \\[4pt]
&=\dfrac{1}{4}x^4-\dfrac{1}{3}x^3-2x^2+4x+C(Cは積分定数)
\end{align*}
ここで,$F(x)=\dfrac{1}{4}x^4-\dfrac{1}{3}x^3-2x^2+4x$ とすると\dint{}{}(f(x)-g(x))\;dx&=\dint{}{}(x^3-x^2-4x+4)\;dx \\[4pt]
&=\dfrac{1}{4}x^4-\dfrac{1}{3}x^3-2x^2+4x+C(Cは積分定数)
\end{align*}
\begin{align*}
S&=\dint{-2}{1}(x^3-x^2-4x+4)\;dx-\dint{1}{2}(x^3-x^2-4x+4)\;dx \\[4pt]
&=\tint{F(x)}{-2}{1}-\tint{F(x)}{1}{2} \\[4pt]
&=F(1)-F(-2)-\{F(2)-F(1)\} \\[4pt]
&=2F(1)-F(-2)-F(2) \\[4pt]
&=2\left(\dfrac{1}{4}-\dfrac{1}{3}-2+4\right)-\left(4+\dfrac{8}{3}-8-8\right)-\left(4-\dfrac{8}{3}-8+8\right) \\[4pt]
&=-\dfrac{1}{6}+4+12-4 \\[4pt]
&=\dfrac{71}{6}
\end{align*}
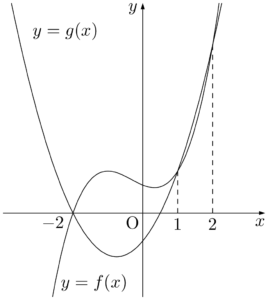
【参考図】S&=\dint{-2}{1}(x^3-x^2-4x+4)\;dx-\dint{1}{2}(x^3-x^2-4x+4)\;dx \\[4pt]
&=\tint{F(x)}{-2}{1}-\tint{F(x)}{1}{2} \\[4pt]
&=F(1)-F(-2)-\{F(2)-F(1)\} \\[4pt]
&=2F(1)-F(-2)-F(2) \\[4pt]
&=2\left(\dfrac{1}{4}-\dfrac{1}{3}-2+4\right)-\left(4+\dfrac{8}{3}-8-8\right)-\left(4-\dfrac{8}{3}-8+8\right) \\[4pt]
&=-\dfrac{1}{6}+4+12-4 \\[4pt]
&=\dfrac{71}{6}
\end{align*}



















