ここでは,直線に関して対称な直線について説明します。
直線は点の集まりであるため,「直線に関して対称な点」を2つ求めることで,直線に関して対称な直線がどのような直線かが分かります。
それほど出題頻度は高くないかもしれませんが,ちゃんと解けるようにしておきましょう。
Contents
直線に関して対称な直線

ヒロ
直線に関して対称な直線の求め方を知ろう。

ヒロ
直線 $l$ を対称軸として,$l$ に関して直線 $m$ と対称な直線を $n$ を求めることを考える。
$l,~m$ が平行でないとき
直線は通る2点を指定することで1つに定まるから,直線 $m$ 上の2点P,Qの $l$ に関して対称な点をそれぞれP$’$,Q$’$ とすると,直線 $n$ は直線P$’$Q$’$ である。
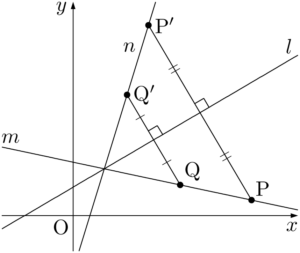
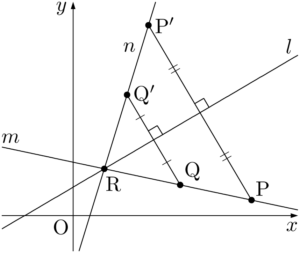
ここで,上では $m$ 上の2点P,Qを適当な位置に選んでいるが,2点のうち1点を $l$ と $m$ の交点Rにとると,その交点の対称点は移動しないから計算が少し楽になる。

ヒロ
直線 $l$ に関して直線 $m$ の対称な直線 $n$ を求めたい場合,次の3つの手順で求めることができる。
対称な直線を求める手順
- 2直線 $l,~m$ の交点Aを求める。
- 直線 $l$ に関する直線 $m$ 上の点Bの対称点B$’$ を求める。
- 2点A,B$’$ を通る直線が求める直線 $n$ である。
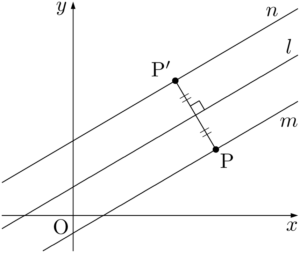
$l,~m$ が平行のとき

ヒロ
このような問題が出ることは少ないと思われるが,説明しておく。
2直線 $l,~m$ が平行のときは,$l$ に関して$m$ 上の2点Pと対称な点P$’$ を通り,$l$ に平行な直線が求める直線 $n$ である。

ヒロ
$l,~m$ が平行のときは,2つの2つの手順で直線 $n$ を求めることができる。
対称な直線を求める手順
- 直線 $l$ に関する直線 $m$ 上の点Pの対称点P$’$ を求める。
- 点P$’$ を通り,$l$ と平行な直線が求める直線 $n$ である。


















