今日は2次式の因数分解について説明します。

とりあえず,やってみよう!
プリントを次のリンクからダウンロードできます。
たすき掛けで横に並べる2数の関係

今まで「因数分解は慣れろ」と言われてきたかもしれないけど,とにかく色々組み合わせを試して見つけろという意味なら,それは嘘だからね。ちゃんとテクニックがあって,それを知ることで大分楽になるからね。

え?簡単にする方法なんてあったんですね!

因数分解で最も基本で重要なことは,共通因数でくくること。だからまずは共通因数の有無を調べよう。

この式だと共通因数はないですね。

そうだね。これでたすき掛けで考えることになるね。まず,掛けて30になる2数を考えるけど,2数の差が小さい組み合わせから考えよう。

ということは,5と6の組み合わせから調べるんですね。

そうだね。次に定数項を見て,一旦符号を無視して,掛けて20になる2数を考えよう。

これは4と5ですね。

問題はこのあとだね。


この2つの組み合わせがあるけど,右の方の組み合わせは計算して確認するまでもなく正しくないことが分かるんだ。

え?計算せずにダメなんてどうして分かるんですか?

仮にこの組み合わせが正しいとすれば,符号を無視すると,$(5x+5)(6x+4)$ と因数分解できることになるよね?でも,これは $5(x+1)\cdot2(3x+2)$ となって,5と2をくくり出せるよね?これっておかしいって分かるかな?

なるほど!最初に共通因数がないって確認したのに,これだと10が共通因数になってしまうので矛盾しますね。

その通り。だからたすき掛けで横に並べる数は互いに素になるようにしなければならないんだ。

ということは,4と5の組み合わせを考えるときは左の組み合わせだけ確認すれば良いってことですね。

実際にたすき掛けを書くと次のようになる。
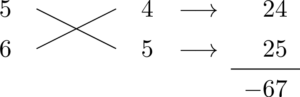

今は符号を無視しているから4と5になってるけど,実際にはどちらかにマイナスが付いているよね?でもどちらにマイナスを付けても $-67$ にできないから,この組み合わせもダメだと分かるんだ。

じゃあ次は左側の数字の組み合わせを変えるんですね。掛けて30だから,3と10を考えます。

右側はどうなるかな?

えっと・・・ $10=2\times5$ だから,10の隣には1しか書けないですね。
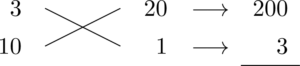

これは明らかにダメですね・・・

そうだね。じゃあ,また左側の数字の組み合わせを変えよう。

次は・・・2と15ですね。2の隣には奇数しか書けないから5で・・・
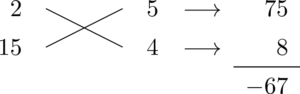

符号を考えると,5の方にマイナスを付ければうまくいきますね。
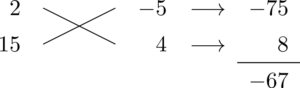
30x^2-67x-20=(2x-5)(15x+4)
\end{align*}

結局3組しか調べてないんですね。

そうだね。では,次の問題にいってみよう。
たすき掛けを極めよう

共通因数はないから,まず,掛けて60になる組み合わせを考えて,6と10から調べていきます。

いや,その組み合わせはあり得ないよ。

え・・・?なんでこの時点で分かるんですか?

それは $x$ の項が奇数だからだよ。

どういうことですか?

今考えた6と10という組み合わせは両方とも偶数だよね。その場合,右側に書く数字が何であっても,たすき掛けで出てくる2数はともに偶数ってことになる。
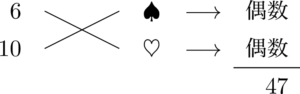

組み合わせをどうしようかと考えるまでもなく,奇数の47にはならないって分かるよね?

なるほど。偶数どうしを足しても引いても偶数にしかならないからですね。$x$ の係数を見ることで左側に書く数字の組み合わせを減らすことが出来るんですね。

そうだね。$x$ の係数が奇数のときには,左側に書く数字の組み合わせに必ず奇数を混ぜないといけないんだ。

ということは,5と12から調べるんですね。

そういうこと!

$12=2^2\times3$ ってことは12の隣は1か5だから・・・
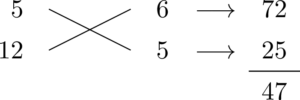

符号を考えて・・・
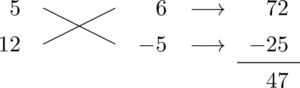
60x^2+47x-30=(5x+6)(12x-5)
\end{align*}

できました!

よし,オッケーだね。

慣れてきました!
たすき掛けからの離脱

じゃあ次はたすき掛けを使わずに因数分解をしよう。

そんなの無理ですよ~!

どうするか説明していくから,聞いといて?

まずは共通因数のチェック。共通因数はないから,掛けて48になる2つの数を考える。その際に $x$ の係数が $-37$ で奇数だから,3と16の組み合わせから考える。ということで,まずこんな風に書こう。
48x^2-37x-36=(3x-\quad)(16x-\quad)
\end{align*}

符号はプラス「$+$」でもマイナス「$-$」でも横棒までは同じなので,符号を書くスペースを確保するためにもマイナスを書いておく。

次に定数項を見て,掛けて36になる2数を考えるが,3の隣に書けるのは3の倍数以外で,16の隣には奇数しか書けない。これを考えて数字を書こう。
48x^2-37x-36=(3x-4)(16x-9)
\end{align*}

こうなるね。定数項が負なので,どちらかに縦棒を加えてプラスにしないといけない。$x$ の係数が $-37$ になるように符号を考えて終わりだね。
48x^2-37x-36=(3x-4)(16x+9)
\end{align*}

なるほど!分かりました!
練習

最後に次の問題をやってみてくれるかな?

やってみますね。
&(3x-\quad)(15x-\quad) \\[4pt]
&(3x-1)(15x-4)\\[4pt]
\end{align*}
45x^2+3x-4=(3x+1)(15x-4)
\end{align*}

おお!すごいね!どうやって考えたの?

共通因数はないので,掛けて45になる2数を考えました。このとき,$x$ の係数が3 (の倍数) で,定数項の素因数には3がないので,両方に3を入れて,3と15に分けました。

次に $x$ の係数が奇数だから,定数項を分けるときに奇数を入れないといけなくて,1と4に分けました。あとは符号を考えて一発でしたね。

そこまで応用できるのは凄いね!
まとめ

たすき掛けで因数分解をするときのコツをまとめておくよ。
- まず,共通因数でくくる。
- 横に並べる2数は互いに素になるようにする。
- 縦に並べる2数は,$x$ の係数を参考にする。

最終的にたすき掛けを使わずにできるようにしよう!



















