ここでは2つの円の交点を通る直線について説明します。
結論だけを公式として覚えることで,問題を解くこともできますが,その成り立ちを理解することも重要だと考えています。
もし,意味も分からず公式を丸暗記する方法で勉強しているのなら今すぐにそんな「間違った勉強法」を辞めて,理解するべき部分についてはしっかり理解するような勉強方法に変えましょう。
Contents
2つの円の交点を通る直線

ヒロ
それでは2つの円の交点を通る直線の方程式の求め方を説明する。
円 $C_1:x^2+y^2+lx+my+n=0$ と円 $C_2:x^2+y^2+px+qy+r=0$ の共有点を通る直線の方程式を求める。
2つの円 $C_1$ と $C_2$ の共有点は,円 $C_1$ 上の点であり,円 $C_2$ 上の点でもある。つまり $C_1,~C_2$ の両方の方程式をみたす $x,~y$ が共有点の座標である。したがって,連立方程式
\begin{align*}
\begin{cases}
x^2+y^2+lx+my+n=0 \\[4pt]
x^2+y^2+px+qy+r=0
\end{cases}
\end{align*}
の解 $(x,~y)$ が $C_1,~C_2$ の共有点の座標である。つまり,共有点の座標を $(X,~Y)$ とすると\begin{cases}
x^2+y^2+lx+my+n=0 \\[4pt]
x^2+y^2+px+qy+r=0
\end{cases}
\end{align*}
\begin{align*}
\begin{cases}
X^2+Y^2+lX+mY+n=0 &~\cdots\cdots① \\[4pt]
X^2+Y^2+pX+qY+r=0 &~\cdots\cdots②
\end{cases}
\end{align*}
が成り立つ。$①-②$ を計算すると\begin{cases}
X^2+Y^2+lX+mY+n=0 &~\cdots\cdots① \\[4pt]
X^2+Y^2+pX+qY+r=0 &~\cdots\cdots②
\end{cases}
\end{align*}
\begin{align*}
&(l-p)X+(m-q)Y+n-r=0~\cdots\cdots③
\end{align*}
となり,これは共有点 $(X,~Y)$ が直線 $(l-p)x+(m-q)y+n-r=0~\cdots\cdots④$ 上にあることを示している。&(l-p)X+(m-q)Y+n-r=0~\cdots\cdots③
\end{align*}
いま,共有点の座標として点 $(X,~Y)$ を考えているが,これは2つの円 $C_1$ と $C_2$ の共有点が1個でも2個でも関係なく,2つの円のすべての共有点の座標に対して③が成り立つから,直線④が2つの円の共有点をすべて(共有点が2個あるときは2個とも)通る直線の方程式である。
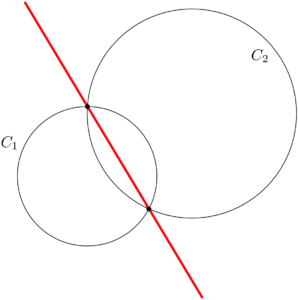

ヒロ
「2つの円の方程式の差をとるだけ」という非常に簡単な結果であるが,その意味をしっかり理解するべきだろう。

ヒロ
また,そもそも2つの円が共有点をもたなければ,2つの円の方程式の差をとって直線の方程式を作ったとしても,何の意味もない。



















