ここでは直線の方程式について説明します。
中学校で学習する基本的な形以外にも,直線の方程式には色々な表し方があります。
与えられた条件に応じて,直線の方程式の求め方を変えられるようになると良いでしょう。
Contents
直線の方程式【基本形】

ヒロ
まずは最も簡単な直線の方程式の基本形の復習をしよう。
【直線の方程式:基本形】
$x$ 軸に垂直ではない直線はすべて $y=ax+b$ の形で表すことができる。ここで $a$ を傾きといい,$b$ を切片($y$ 切片)という。傾きが $a$ とは,$x$ が1増加するとき,$y$ が $a$ 増加することを表している。また $y$ 切片が $b$ とは,グラフが点 $(0,~b)$ を通ることを表している。
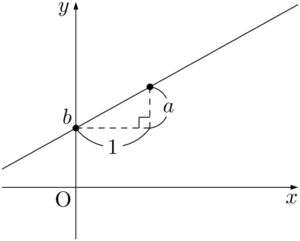
基本形では,$x$ 軸に垂直な直線を表すことはできない。
$x$ 軸に垂直ではない直線はすべて $y=ax+b$ の形で表すことができる。ここで $a$ を傾きといい,$b$ を切片($y$ 切片)という。傾きが $a$ とは,$x$ が1増加するとき,$y$ が $a$ 増加することを表している。また $y$ 切片が $b$ とは,グラフが点 $(0,~b)$ を通ることを表している。

基本形では,$x$ 軸に垂直な直線を表すことはできない。
直線の方程式【切片形】

ヒロ
$x$ 切片と $y$ 切片を利用した形が切片形である。
【直線の方程式:切片形】
座標軸上の2点 $(a,~0)$,$(0,~b)$ を通る直線の方程式は $\dfrac{x}{a}+\dfrac{y}{b}=1$ である。
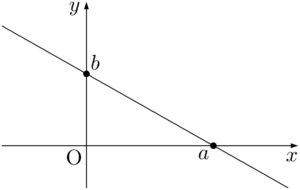
切片形で表された直線では,座標軸に垂直な直線を表すことはできない。
座標軸上の2点 $(a,~0)$,$(0,~b)$ を通る直線の方程式は $\dfrac{x}{a}+\dfrac{y}{b}=1$ である。

切片形で表された直線では,座標軸に垂直な直線を表すことはできない。
直線の方程式【一般形】

ヒロ
$x$ 軸に垂直な直線も表せる形が一般形となる。
【直線の方程式:一般形】
直線の方程式は必ず $ax+by+c=0$ の形で表すことができる。ただし,$a$ と $b$ が同時に0になることはないとする。
(i) $a=0$ のとき,$y=-\dfrac{c}{b}$ となり,$x$ 軸に平行な直線となる。
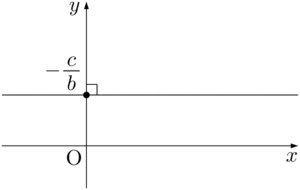
(ii) $b=0$ のとき,$x=-\dfrac{c}{a}$ となり,$x$ 軸に垂直な直線となる。
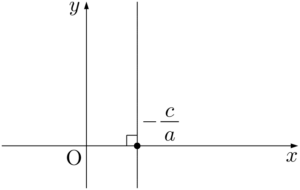
(iii) $a$ も $b$ も0でないとき,点 $\left(0,~-\dfrac{c}{b}\right)$ を通り,傾き $-\dfrac{b}{a}$ の直線となる。

直線の方程式は必ず $ax+by+c=0$ の形で表すことができる。ただし,$a$ と $b$ が同時に0になることはないとする。
(i) $a=0$ のとき,$y=-\dfrac{c}{b}$ となり,$x$ 軸に平行な直線となる。

(ii) $b=0$ のとき,$x=-\dfrac{c}{a}$ となり,$x$ 軸に垂直な直線となる。

(iii) $a$ も $b$ も0でないとき,点 $\left(0,~-\dfrac{c}{b}\right)$ を通り,傾き $-\dfrac{b}{a}$ の直線となる。

直線の方程式の求め方

ヒロ
状況に応じて,できるだけ楽になるように直線の方程式を求めよう。

ヒロ
答えの形が決められているときは,とりあえず直線の方程式を求めてから変形すれば良い。
通る1点と傾きが与えられているとき

ヒロ
通る1点と傾きが与えられているときは,基本形で求めるのが良いだろう。
【基本形の直線の方程式】
点 $(p,~q)$ を通り,傾きが $m$ の直線の方程式を求める。傾きが $m$ だから,
点 $(p,~q)$ を通り,傾きが $m$ の直線の方程式を求める。傾きが $m$ だから,
\begin{align*}
y=mx+\cdots
\end{align*}
の形になるはずである。ここで,点 $(p,~q)$ を通るから,$x$ に $p$ を代入したときに $y=q$ になることを考えると,y=mx+\cdots
\end{align*}
\begin{align*}
y=m(x-p)+q
\end{align*}
となる。もう少し丁寧に説明をしておく。$x=p$ を代入したときに一旦 $y=0$ となるように $y=m(x-p)+\cdots$ という形にする。しかし,実際にはそのときの $y$ の値は $q$ であるから,後ろに $q$ を付けておく。y=m(x-p)+q
\end{align*}
基本形の直線の方程式点 $(p,~q)$ を通り,傾きが $m$ の直線の方程式は
\begin{align*}
y=m(x-p)+q
\end{align*}
となる。y=m(x-p)+q
\end{align*}
通る2点が与えられているとき

ヒロ
与えられた2点の座標に応じて,直線の方程式を求めよう。
【与えられた2点の座標に着目する】
(i) 2点の $x$ 座標が等しい($p$ とする)とき
その直線は $x$ 軸に垂直な直線で,方程式は $x=p$ である。
(ii) 2点の $y$ 座標が等しい($q$ とする)とき
その直線は $x$ 軸に平行な直線で,方程式は $y=q$ である。
(iii) (i),(ii)以外のとき
与えられた2点の座標を $(p,~q)$,$(r,~s)$ として,直線の傾きを $m$ とする。まずは傾き $m$ を求めよう。
(i) 2点の $x$ 座標が等しい($p$ とする)とき
その直線は $x$ 軸に垂直な直線で,方程式は $x=p$ である。
(ii) 2点の $y$ 座標が等しい($q$ とする)とき
その直線は $x$ 軸に平行な直線で,方程式は $y=q$ である。
(iii) (i),(ii)以外のとき
与えられた2点の座標を $(p,~q)$,$(r,~s)$ として,直線の傾きを $m$ とする。まずは傾き $m$ を求めよう。
\begin{align*}
m=\dfrac{q-s}{p-r}
\end{align*}
あとは通る1点と傾きが与えられた状態と同じだからm=\dfrac{q-s}{p-r}
\end{align*}
\begin{align*}
y=m(x-p)+q
\end{align*}
となる。点 $(r,~s)$ を通るとしてy=m(x-p)+q
\end{align*}
\begin{align*}
y=m(x-r)+s
\end{align*}
としても良い。どちらの点を使っても,同じ式になる。y=m(x-r)+s
\end{align*}
直線の方程式を求める問題【東洋大】
2018年 東洋大2点P$(-4,~5)$,Q$(1,~-1)$ を通る直線の方程式は $y=-\dfrac{\myhako}{\myhako}x+\dfrac{1}{\myhako}$ である。
【考え方と解答】
2点P,Qの $x$ 座標と $y$ 座標はどちらも等しくないから,まず傾きを求める。
直線PQの傾きは
2点P,Qの $x$ 座標と $y$ 座標はどちらも等しくないから,まず傾きを求める。
直線PQの傾きは
\begin{align*}
\dfrac{5-(-1)}{-4-1}=-\dfrac{6}{5}
\end{align*}
であるから,直線PQの方程式は\dfrac{5-(-1)}{-4-1}=-\dfrac{6}{5}
\end{align*}
\begin{align*}
&y=-\dfrac{6}{5}(x-1)-1 \\[4pt]
&y=-\dfrac{6}{5}x+\dfrac{1}{5}
\end{align*}
&y=-\dfrac{6}{5}(x-1)-1 \\[4pt]
&y=-\dfrac{6}{5}x+\dfrac{1}{5}
\end{align*}


















