ここでは三角比の変形を利用した問題について解説します。
90°±θや180°-θの三角比の変形を利用することで,どのような三角比も45°以下の角の三角比で表すことができるようになります。
この記事を読むことで,どの公式を利用するかの判断が簡単にできるようになります。
「グラグラするとかしないとか」を知らない人は次の記事から知識を手に入れましょう。
得意な問題をどんどん増やしていきましょう。
Contents
45°以下の角の三角比で表す方法

ヒロ
三角比の変形の公式を利用することで,鈍角の三角比を鋭角で表したり,さらに単に鋭角ということでなく,45°以下の三角比で表すことができる。
【利用する公式の見分け方】
「$90\Deg\pm\theta$ や $180\Deg-\theta$ の公式を利用しよう」と言われても,どの公式を利用すれば良いかがすぐに判断できない人もいるだろう。利用する公式に迷うことがなくなるように,意識するべきポイントを知っておこう。45°以下の角の三角比で表すためには,扱っている角度に最も近い座標軸がどこなのかをすぐに判断できるようにするべきである。そのためには視覚的に判断するのが良いだろう。
0°~180°を45°刻みで分割すると,次の図のように,ピンク・青・緑・赤の4つの部分に分けられる。
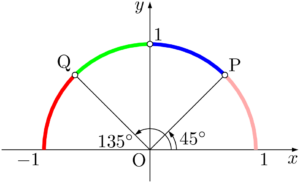
扱っている角がピンクの部分にあるときは,最初から45°以下であるから変形する必要がない。青の部分にあるときは, $y$ 軸が最も近い座標軸であるから,$90\Deg-\theta$ の公式を利用しよう。緑の部分にあるときは,$90\Deg+\theta$ の公式を利用しよう。最後に,赤の部分にあるときは,$x$ 軸が最も近い座標軸であるから,$180\Deg-\theta$ の公式を利用しよう。
「$90\Deg\pm\theta$ や $180\Deg-\theta$ の公式を利用しよう」と言われても,どの公式を利用すれば良いかがすぐに判断できない人もいるだろう。利用する公式に迷うことがなくなるように,意識するべきポイントを知っておこう。45°以下の角の三角比で表すためには,扱っている角度に最も近い座標軸がどこなのかをすぐに判断できるようにするべきである。そのためには視覚的に判断するのが良いだろう。
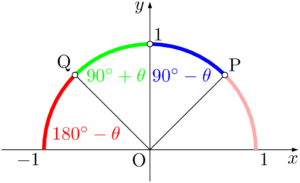
0°~180°を45°刻みで分割すると,次の図のように,ピンク・青・緑・赤の4つの部分に分けられる。

扱っている角がピンクの部分にあるときは,最初から45°以下であるから変形する必要がない。青の部分にあるときは, $y$ 軸が最も近い座標軸であるから,$90\Deg-\theta$ の公式を利用しよう。緑の部分にあるときは,$90\Deg+\theta$ の公式を利用しよう。最後に,赤の部分にあるときは,$x$ 軸が最も近い座標軸であるから,$180\Deg-\theta$ の公式を利用しよう。