ここでは,2次関数のグラフ(放物線)の対称移動について説明します。
対称移動には,点に関する対称移動と直線に関する対称移動があります。
どのような対称移動にも対応できるようにしておきましょう。
放物線の対称移動

ヒロ
まず,そもそも「対称移動」とはどういう移動かを知っておこう。
対称移動平面上で,図形上の各点を,直線や点に関してそれと対称な位置に移すことを対称移動という。

ヒロ
主に,$x$ 軸や $y$ 軸を対称の軸として線対称な位置に移す対称移動と,原点を対称の中心として点対称な位置に移す対称移動に関する問題が多い。

ヒロ
ポイントを先にまとめておくと次のようになる。
$y=f(x)$ の対称移動
- $x$ 軸:$y=-f(x)$
- $y$ 軸:$y=f(-x)$
- 原点:$y=-f(-x)$

ヒロ
一般的な関数 $y=f(x)$ の対称移動を考えて,順番に説明していく。
$x$ 軸に関する対称移動
【$x$ 軸に関する対称移動】
$y=f(x)$ 上の点 $\text{P}(x,~y)$ を $x$ 軸に関して対称移動させたときに点 $\text{Q}(X,~Y)$ に移るとすると
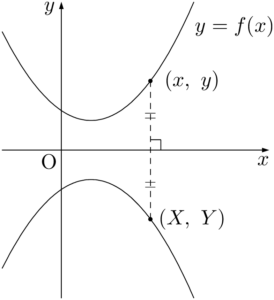
$y=f(x)$ 上の点 $\text{P}(x,~y)$ を $x$ 軸に関して対称移動させたときに点 $\text{Q}(X,~Y)$ に移るとすると
\begin{align*}
&X=x,~Y=-y \\[4pt]
&x=X,~y=-Y
\end{align*}
$y=f(x)$ に代入して&X=x,~Y=-y \\[4pt]
&x=X,~y=-Y
\end{align*}
\begin{align*}
&-Y=f(X) \\[4pt]
&Y=-f(X)
\end{align*}
これは点Qが $y=-f(x)$ 上にあることを示している。&-Y=f(X) \\[4pt]
&Y=-f(X)
\end{align*}

$y$ 軸に関する対称移動
【$y$ 軸に関する対称移動】
$y=f(x)$ 上の点 $\text{P}(x,~y)$ を $y$ 軸に関して対称移動させたときに点 $\text{Q}(X,~Y)$ に移るとすると
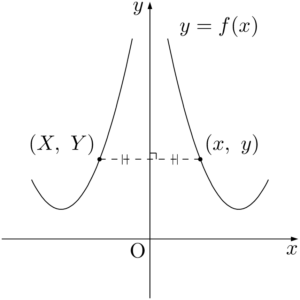
$y=f(x)$ 上の点 $\text{P}(x,~y)$ を $y$ 軸に関して対称移動させたときに点 $\text{Q}(X,~Y)$ に移るとすると
\begin{align*}
&X=-x,~Y=y \\[4pt]
&x=-X,~y=Y
\end{align*}
$y=f(x)$ に代入して&X=-x,~Y=y \\[4pt]
&x=-X,~y=Y
\end{align*}
\begin{align*}
&Y=f(-X)
\end{align*}
これは点Qが $y=f(-x)$ 上にあることを示している。&Y=f(-X)
\end{align*}

原点に関する対称移動
【$x$ 軸に関する対称移動】
$y=f(x)$ 上の点 $\text{P}(x,~y)$ を原点に関して対称移動させたときに点 $\text{Q}(X,~Y)$ に移るとすると
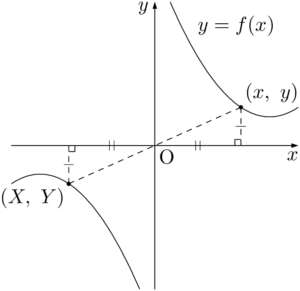
$y=f(x)$ 上の点 $\text{P}(x,~y)$ を原点に関して対称移動させたときに点 $\text{Q}(X,~Y)$ に移るとすると
\begin{align*}
&X=-x,~Y=-y \\[4pt]
&x=-X,~y=-Y
\end{align*}
$y=f(x)$ に代入して&X=-x,~Y=-y \\[4pt]
&x=-X,~y=-Y
\end{align*}
\begin{align*}
&-Y=f(-X) \\[4pt]
&Y=-f(-X)
\end{align*}
これは点Qが $y=-f(-x)$ 上にあることを示している。&-Y=f(-X) \\[4pt]
&Y=-f(-X)
\end{align*}

放物線の対称移動に関する問題

ヒロ
それでは実際に定期テストで出題された問題を解いてみよう。
問題放物線 $y=3x^2+x-7$ を,次の直線または点に関して,それぞれ対称移動して得られる放物線の方程式を求めよ。
(1) $x$ 軸
(2) $y$ 軸
(3) 原点
(1) $x$ 軸
(2) $y$ 軸
(3) 原点

ヒロ
上でまとめたポイントを見て解くのではなく,ポイントを見ずに解けるようにしよう。
【考え方と解答】
(1) $x$ 軸に関して対称移動するとき,$y$ 座標の符号が変わるから
(1) $x$ 軸に関して対称移動するとき,$y$ 座標の符号が変わるから
\begin{align*}
y&=-(3x^2+x-7) \\[4pt]
&=-3x^2-x+7
\end{align*}
(2) $y$ 軸に関して対称移動するとき,$x$ 座標の符号が変わるからy&=-(3x^2+x-7) \\[4pt]
&=-3x^2-x+7
\end{align*}
\begin{align*}
y&=3(-x)^2+(-x)-7 \\[4pt]
&=3x^2-x-7
\end{align*}
(3) 原点に関して対称移動するとき,$x$ 座標と $y$ 座標の符号が変わるからy&=3(-x)^2+(-x)-7 \\[4pt]
&=3x^2-x-7
\end{align*}
\begin{align*}
y&=-\{3(-x)^2+(-x)-7\} \\[4pt]
&=-3x^2+x+7
\end{align*}
y&=-\{3(-x)^2+(-x)-7\} \\[4pt]
&=-3x^2+x+7
\end{align*}


















