ここでは異なるもので数珠(じゅず)を作る方法の総数を求める方法や考え方について説明します。
数珠を作るときには,円順列と同様に回転すると同じ並び方になるものはすべて同じ順列として扱うことに加えて,裏返すと同じ並び方になるものも同じ順列として扱うことに注意する必要があります。
「数珠順列の公式」というものがありますが,円順列の公式と同じように,公式がないと生きていけない人向けのものという認識です。
公式を知っているだけでは解けない問題は多くあるため,学校の定期テスト程度の問題なら通用しても,大学入試に出題される問題を解くことはできません。
難問に対応するためにも,まずは基本的な考え方を身に付けましょう。
数珠を作るのは円形に並べるのと何が異なるのか?

ヒロ
例えば1, 2, 3, 4, 5, 6が書かれた6つの玉をすべて使って数珠を作ることを考える。
【数珠を作るときの考え方】
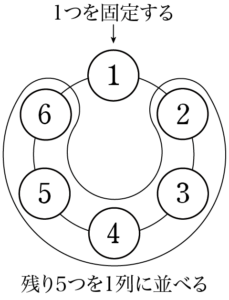
円順列と同様に,回転しないように1つを固定しよう。例えば1が書かれた玉を固定する。残り5つの玉を1列に並べる方法が $5!=120$ 通りあるから,円順列の総数は120通りである。
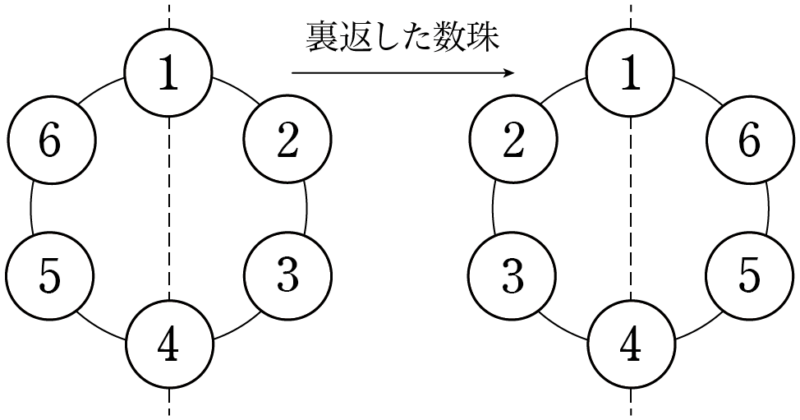
いまは数珠を作ることを考えているから,裏返すと同じ数珠になるものを同じ順列として扱うことに注意する。左右対称になる円順列の組は円順列では2通りとして数えても,数珠順列としては1通りとして数えるため,円順列の総数を「2で割る」ことで数珠順列の総数を求めることができる。
よって,異なる6つの玉をすべて使ってできる数珠の総数は
円順列と同様に,回転しないように1つを固定しよう。例えば1が書かれた玉を固定する。残り5つの玉を1列に並べる方法が $5!=120$ 通りあるから,円順列の総数は120通りである。

いまは数珠を作ることを考えているから,裏返すと同じ数珠になるものを同じ順列として扱うことに注意する。左右対称になる円順列の組は円順列では2通りとして数えても,数珠順列としては1通りとして数えるため,円順列の総数を「2で割る」ことで数珠順列の総数を求めることができる。

よって,異なる6つの玉をすべて使ってできる数珠の総数は
\begin{align*}
\dfrac{5!}{2}=60~通り
\end{align*}
\dfrac{5!}{2}=60~通り
\end{align*}

ヒロ
一応,公式を載せておくと次のようになる。
数珠順列異なる $n$ 個のもので数珠を作る方法の総数は $\dfrac{(n-1)!}{2}$ 通り。
定期テストで出題された問題

ヒロ
それでは実際に定期テストで出題された問題を解いてみよう。
問題色の異なる5つの玉をつないで,ブレスレットを作る方法は何通りあるか。
【考え方と解答】
問題文に「ブレスレット」とあるから,「表と裏が関係ないもの」だと認識しよう。
1つの玉を固定して,残り4つの玉を並べる方法が $4!$ 通りある。裏返すと同じブレスレットになるものを考えて,求める場合の数は
問題文に「ブレスレット」とあるから,「表と裏が関係ないもの」だと認識しよう。
1つの玉を固定して,残り4つの玉を並べる方法が $4!$ 通りある。裏返すと同じブレスレットになるものを考えて,求める場合の数は
\begin{align*}
\dfrac{4!}{2}=12~通り
\end{align*}
\dfrac{4!}{2}=12~通り
\end{align*}


















