大学入試では,整数の和が3の倍数になる条件に関する問題をよく目にします。
「$n$ 回」「3の倍数」「確率」の3つを見た途端「これは無理だ」と思って諦めることのないように,しっかり対策することが重要です。
ここでは2013年に東北大で出題された確率の問題を扱い,3の倍数に関する問題の解法や状態遷移図を用いた考え方を説明します。
2013年 東北大

ヒロ
それでは次の問題を解いてみよう。
2013年 東北大袋の中に $\{1,2,3,4,5\}$ の番号が1つずつ書かれた5つの玉が入っている。この中から無作為に1個の玉を取り出し,玉に書かれている数字を記録したのち袋に戻すという操作を行う。その操作を繰り返し,記録された数字の和が3の倍数になった時点で終了する。ただし,1回目で3の倍数が出た場合は,その時点で終了とする。$n$ 回目の操作で終了する確率を $p_n$ とする。
(1) $p_1,~p_2$ を求めよ。
(2) $n\geqq3$ のとき,$p_n$ を $n$ の式で表せ。
(1) $p_1,~p_2$ を求めよ。
(2) $n\geqq3$ のとき,$p_n$ を $n$ の式で表せ。
(1)考え方と解答

ヒロ
(1)は具体的に確率を求める問題だから,しっかり得点したいね。
【(1) $p_1$ の解答】
$p_1$ は1回目の操作で終了する確率である。
1回目の操作で終了するのは,1回目に3と書かれた玉を取り出すときだから
$p_1$ は1回目の操作で終了する確率である。
1回目の操作で終了するのは,1回目に3と書かれた玉を取り出すときだから
\begin{align*}
p_1=\dfrac{1}{5}
\end{align*}
p_1=\dfrac{1}{5}
\end{align*}

ヒロ
次は2つの数字の和が3の倍数になるときを考えよう。
【(1) $p_2$ の解答】
取り出した玉の組み合わせを $(1回目,~2回目)$ と表すことにすると,条件を満たす組み合わせを書き並べると次のようになる。
取り出した玉の組み合わせを $(1回目,~2回目)$ と表すことにすると,条件を満たす組み合わせを書き並べると次のようになる。
\begin{align*}
&(1,~2),~(1,~5),~(2,~1),~(2,~4) \\[4pt]
&(4,~2),~(4,~5),~(5,~1),~(5,~4)
\end{align*}
したがって&(1,~2),~(1,~5),~(2,~1),~(2,~4) \\[4pt]
&(4,~2),~(4,~5),~(5,~1),~(5,~4)
\end{align*}
\begin{align*}
p_2=8\times\left(\dfrac{1}{5}\right)^2=\dfrac{8}{25}
\end{align*}
p_2=8\times\left(\dfrac{1}{5}\right)^2=\dfrac{8}{25}
\end{align*}
(2)考え方と解答
(2) $n\geqq3$ のとき,$p_n$ を $n$ の式で表せ。

(1)みたいに具体的に書き並べる方法だと解けないですよね?

ヒロ
そうだね。こういうときは終了する直前の状態に着目して状態遷移図を考えよう。

「終了する直前」って言われても,その和なんて分かりません。

ヒロ
いまは「和が3の倍数」になった時点で終了するときを考えるのだから,その直前は,それまでの和は3の倍数ではないね。

なるほど。

ヒロ
つまり3で割った余りに着目しよう。

$n-1$ 回の操作終了後までは3で割った余りが1か2の状態にあって,$n$ 回目の操作終了後に3で割った余りが0になれば良いってことですね。

ヒロ
完璧だね。
【(2)の解答】
数字の和を3で割ったときの余りを $X$ で表すと,状態遷移図は次の図のようになる。
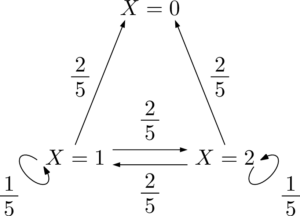
したがって,$n\geqq3$ のとき,$n$ 回目の操作で終了するのは,1回目には3以外が出て,$n-2$ 回は毎回確率 $\dfrac35$ で終了しない数が出て,$n$ 回目に確率 $\dfrac25$ で終了する数が出るときであるから,
数字の和を3で割ったときの余りを $X$ で表すと,状態遷移図は次の図のようになる。
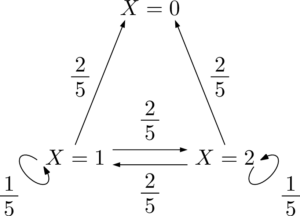
したがって,$n\geqq3$ のとき,$n$ 回目の操作で終了するのは,1回目には3以外が出て,$n-2$ 回は毎回確率 $\dfrac35$ で終了しない数が出て,$n$ 回目に確率 $\dfrac25$ で終了する数が出るときであるから,
\begin{align*}
&p_n=\dfrac45\left(\dfrac35\right)^{n-2}\Cdota\dfrac25 \\
&p_n=\dfrac8{25}\left(\dfrac35\right)^{n-2}
\end{align*}
&p_n=\dfrac45\left(\dfrac35\right)^{n-2}\Cdota\dfrac25 \\
&p_n=\dfrac8{25}\left(\dfrac35\right)^{n-2}
\end{align*}

ヒロ
今回は漸化式を立てなくても解ける問題だったね。

ヒロ
次のように漸化式を立てて解く練習をしておくのも良いだろう。
【(2)の別解】
数字の和を3で割ったときの余りを $X$ とする。
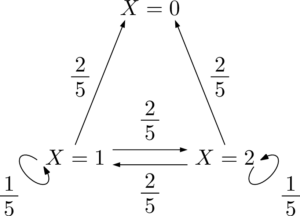
$k$ 回の操作終了後 $X=1$ である確率を $q_k$,$X=2$ である確率を $r_k$ とすると,
$q_1=r_1=\dfrac25$ だから,
数字の和を3で割ったときの余りを $X$ とする。
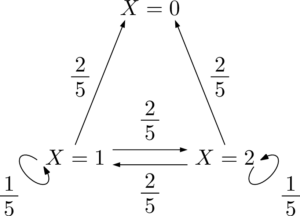
$k$ 回の操作終了後 $X=1$ である確率を $q_k$,$X=2$ である確率を $r_k$ とすると,
\begin{align*}
\begin{cases}
p_{k+1}=\dfrac25q_k+\dfrac25r_k~&\cdots\cdots① \\[7pt]
q_{k+1}=\dfrac15q_k+\dfrac25r_k~&\cdots\cdots② \\[7pt]
r_{k+1}=\dfrac15r_k+\dfrac25q_k~&\cdots\cdots③
\end{cases}
\end{align*}
$②+③$より,\begin{cases}
p_{k+1}=\dfrac25q_k+\dfrac25r_k~&\cdots\cdots① \\[7pt]
q_{k+1}=\dfrac15q_k+\dfrac25r_k~&\cdots\cdots② \\[7pt]
r_{k+1}=\dfrac15r_k+\dfrac25q_k~&\cdots\cdots③
\end{cases}
\end{align*}
\begin{align*}
q_{k+1}+r_{k+1}=\dfrac35(q_k+r_k)
\end{align*}
数列 $\{q_k+r_k\}$ は公比 $\dfrac35$ の等比数列で,q_{k+1}+r_{k+1}=\dfrac35(q_k+r_k)
\end{align*}
$q_1=r_1=\dfrac25$ だから,
\begin{align*}
q_{n-1}+r_{n-1}&=(q_1+r_1)\left(\dfrac35\right)^{n-2} \\[4pt]
&=\dfrac45\left(\dfrac35\right)^{n-2}
\end{align*}
①より,q_{n-1}+r_{n-1}&=(q_1+r_1)\left(\dfrac35\right)^{n-2} \\[4pt]
&=\dfrac45\left(\dfrac35\right)^{n-2}
\end{align*}
\begin{align*}
p_n&=\dfrac25(q_{n-1}+r_{n-1}) \\[4pt]
&=\dfrac25\Cdota\dfrac45\left(\dfrac35\right)^{n-2} \\[4pt]
&=\dfrac8{25}\left(\dfrac35\right)^{n-2}
\end{align*}
p_n&=\dfrac25(q_{n-1}+r_{n-1}) \\[4pt]
&=\dfrac25\Cdota\dfrac45\left(\dfrac35\right)^{n-2} \\[4pt]
&=\dfrac8{25}\left(\dfrac35\right)^{n-2}
\end{align*}


















