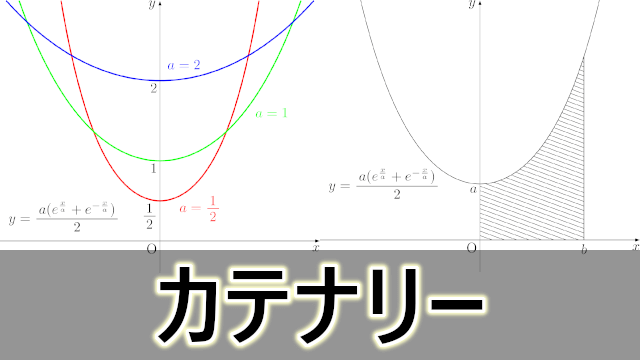
ロープやチェーンなどの両端を持って垂らしたときにできる曲線をカテナリー(懸垂線)といい,$y=\dfrac{a(e^{\frac{x}{a}}+e^{-\frac{x}{a}})}{2}$ と表されます。$a=\dfrac{1}{2},~1,~2$ のときを図示すると次のようになります。
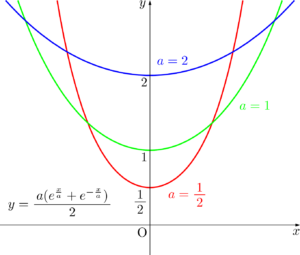
かなり高い頻度で入試に出題されるため,グラフの描画,曲線の長さ,面積,回転体の体積などを求める計算に慣れておきましょう。
カテナリー曲線の描画

ヒロ
増減表を書いてカテナリー曲線を描こう。
$f(x)=\dfrac{a(e^{\frac{x}{a}}+e^{-\frac{x}{a}})}{2}$ より
\begin{align*}
&f'(x)=\dfrac{e^{\frac{x}{a}}-e^{-\frac{x}{a}}}{2}=\dfrac{e^{-\frac{x}{a}}(e^{\frac{2x}{a}}-1)}{2} \\[4pt]
&f^{\prime\prime}(x)=\dfrac{e^{\frac{x}{a}}+e^{-\frac{x}{a}}}{2a}>0
\end{align*}
$f'(x)=0$ とすると&f'(x)=\dfrac{e^{\frac{x}{a}}-e^{-\frac{x}{a}}}{2}=\dfrac{e^{-\frac{x}{a}}(e^{\frac{2x}{a}}-1)}{2} \\[4pt]
&f^{\prime\prime}(x)=\dfrac{e^{\frac{x}{a}}+e^{-\frac{x}{a}}}{2a}>0
\end{align*}
\begin{align*}
&e^{\frac{2x}{a}}=1 \\[4pt]
&x=0
\end{align*}
&e^{\frac{2x}{a}}=1 \\[4pt]
&x=0
\end{align*}
| $x$ | $\cdots$ | $0$ | $\cdots$ |
| $f'(x)$ | $-$ | $0$ | $+$ |
| $f^{\prime\prime}(x)$ | $+$ | $+$ | $+$ |
| $f(x)$ | ⤴ |
$a$ | ⤴ |
増減表より,グラフは次のようになる。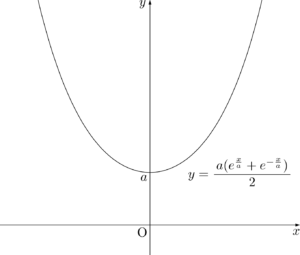
カテナリー曲線の長さ

ヒロ
カテナリー曲線の $0\leqq x\leqq b$ の部分の長さ $L$ を求めよう。
$f'(x)=\dfrac{e^{\frac{x}{a}}-e^{-\frac{x}{a}}}{2}$ より,
\begin{align*}
1+\{f'(x)\}^2&=1+\left(\dfrac{e^{\frac{x}{a}}-e^{-\frac{x}{a}}}{2}\right)^2 \\[4pt]
&=\left(\dfrac{e^{\frac{x}{a}}+e^{-\frac{x}{a}}}{2}\right)^2
\end{align*}
$\dfrac{e^{\frac{x}{a}}+e^{-\frac{x}{a}}}{2}>0$ より1+\{f'(x)\}^2&=1+\left(\dfrac{e^{\frac{x}{a}}-e^{-\frac{x}{a}}}{2}\right)^2 \\[4pt]
&=\left(\dfrac{e^{\frac{x}{a}}+e^{-\frac{x}{a}}}{2}\right)^2
\end{align*}
\begin{align*}
L&=\dint{0}{b}\sqrt{1+\{f'(x)\}^2}\;dx \\[4pt]
&=\dint{0}{b}\dfrac{e^{\frac{x}{a}}+e^{-\frac{x}{a}}}{2}\;dx \\[4pt]
&=\Tint{\dfrac{a(e^{\frac{x}{a}}-e^{-\frac{x}{a}})}{2}}{0}{b} \\[4pt]
&=\dfrac{a(e^{\frac{b}{a}}-e^{-\frac{b}{a}})}{2}
\end{align*}
L&=\dint{0}{b}\sqrt{1+\{f'(x)\}^2}\;dx \\[4pt]
&=\dint{0}{b}\dfrac{e^{\frac{x}{a}}+e^{-\frac{x}{a}}}{2}\;dx \\[4pt]
&=\Tint{\dfrac{a(e^{\frac{x}{a}}-e^{-\frac{x}{a}})}{2}}{0}{b} \\[4pt]
&=\dfrac{a(e^{\frac{b}{a}}-e^{-\frac{b}{a}})}{2}
\end{align*}

ヒロ
$f'(x)=\dfrac{e^{\frac{x}{a}}-e^{-\frac{x}{a}}}{2}$ より,$L=af'(b)$ と表すことができる。
カテナリー曲線と面積

ヒロ
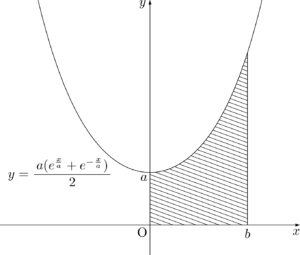
カテナリー曲線と座標軸,直線 $x=b$ で囲まれる部分の面積 $S$ を求めよう。
図の斜線部分の面積が $S$ である。

\begin{align*}
S&=\dint{0}{b}f(x)\;dx \\[4pt]
&=a\dint{0}{b}\dfrac{e^{\frac{x}{a}}+e^{-\frac{x}{a}}}{2}\;dx \\[4pt]
&=aL \\[4pt]
&=\dfrac{a^2(e^{\frac{b}{a}}-e^{-\frac{b}{a}})}{2}
\end{align*}
S&=\dint{0}{b}f(x)\;dx \\[4pt]
&=a\dint{0}{b}\dfrac{e^{\frac{x}{a}}+e^{-\frac{x}{a}}}{2}\;dx \\[4pt]
&=aL \\[4pt]
&=\dfrac{a^2(e^{\frac{b}{a}}-e^{-\frac{b}{a}})}{2}
\end{align*}

ヒロ
$f'(x)=\dfrac{e^{\frac{x}{a}}-e^{-\frac{x}{a}}}{2}$ より,$S=a^2f'(b)$ と表すことができる。
カテナリー曲線の回転体の体積

ヒロ
カテナリー曲線の $0\leqq x\leqq b$ の部分を $x$ 軸のまわりに1回転させてできる立体の体積 $V$ を求めよう。
求める立体の体積 $V$ は
\begin{align*}
V&=\dint{0}{b}\pi\{f(x)\}^2\;dx \\[4pt]
&=\pi\dint{0}{b}\left(\dfrac{a(e^{\frac{x}{a}}+e^{-\frac{x}{a}})}{2}\right)^2\;dx \\[4pt]
&=\dfrac{\pi a^2}{4}\dint{0}{b}\left(e^{\frac{2x}{a}}+e^{-\frac{2x}{a}}+2\right)\;dx \\[4pt]
&=\dfrac{\pi a^2}{4}\Tint{\dfrac{a}{2}(e^{\frac{2x}{a}}-e^{-\frac{2x}{a}})+2x}{0}{b} \\[4pt]
&=\dfrac{\pi a^2}{8}\left\{a(e^{\frac{2b}{a}}-e^{-\frac{2b}{a}})+4b\right\}
\end{align*}
V&=\dint{0}{b}\pi\{f(x)\}^2\;dx \\[4pt]
&=\pi\dint{0}{b}\left(\dfrac{a(e^{\frac{x}{a}}+e^{-\frac{x}{a}})}{2}\right)^2\;dx \\[4pt]
&=\dfrac{\pi a^2}{4}\dint{0}{b}\left(e^{\frac{2x}{a}}+e^{-\frac{2x}{a}}+2\right)\;dx \\[4pt]
&=\dfrac{\pi a^2}{4}\Tint{\dfrac{a}{2}(e^{\frac{2x}{a}}-e^{-\frac{2x}{a}})+2x}{0}{b} \\[4pt]
&=\dfrac{\pi a^2}{8}\left\{a(e^{\frac{2b}{a}}-e^{-\frac{2b}{a}})+4b\right\}
\end{align*}
カテナリーに関する入試問題

ヒロ
実際に出題された入試問題を解いてみよう。
2018年 北九州市立大曲線 $C:y=\dfrac{e^x+e^{-x}}{2}$ について,以下の問いに答えよ。
(1) 曲線 $C$ の極値,グラフの凹凸,及び変曲点を調べて,増減表を作成せよ。
(2) 曲線 $C$ のグラフをかけ。
(3) 曲線 $C$ と直線 $y=0$,及び,直線 $x=-1$ と直線 $x=1$ に囲まれた図形の面積 $S$ を求めよ。
(4) 曲線 $C$ において,区間 $-1\leqq x\leqq1$ の長さ $L$ を求めよ。
(1) 曲線 $C$ の極値,グラフの凹凸,及び変曲点を調べて,増減表を作成せよ。
(2) 曲線 $C$ のグラフをかけ。
(3) 曲線 $C$ と直線 $y=0$,及び,直線 $x=-1$ と直線 $x=1$ に囲まれた図形の面積 $S$ を求めよ。
(4) 曲線 $C$ において,区間 $-1\leqq x\leqq1$ の長さ $L$ を求めよ。

ヒロ
微分して増減表を作ろう。
【(1)の解答】
$y=\dfrac{e^x+e^{-x}}{2}$ より
$y=\dfrac{e^x+e^{-x}}{2}$ より
\begin{align*}
&y’=\dfrac{e^x-e^{-x}}{2}=\dfrac{e^{-x}(e^{2x}-1)}{2} \\[4pt]
&y^{\prime\prime}=\dfrac{e^x+e^{-x}}{2}>0
\end{align*}
$y’=0$ とすると&y’=\dfrac{e^x-e^{-x}}{2}=\dfrac{e^{-x}(e^{2x}-1)}{2} \\[4pt]
&y^{\prime\prime}=\dfrac{e^x+e^{-x}}{2}>0
\end{align*}
\begin{align*}
&e^{2x}-1=0 \\[4pt]
&x=0
\end{align*}
よって,増減は次のようになる。
&e^{2x}-1=0 \\[4pt]
&x=0
\end{align*}
| $x$ | $\cdots$ | $0$ | $\cdots$ |
| $y’$ | $-$ | $0$ | $+$ |
| $y^{\prime\prime}$ | $+$ | $+$ | $+$ |
| $y$ | ⤴ |
$1$ | ⤴ |
$x=0$ で極小値1をとる。変曲点はない。

ヒロ
増減表があるからグラフは簡単。
【(2)の解答】
増減表より,曲線 $C$ のグラフは次のようになる。
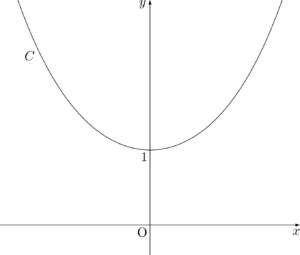
増減表より,曲線 $C$ のグラフは次のようになる。


ヒロ
次は面積だね。
【(3)の解答】
$S$ は図の斜線部分の面積である。
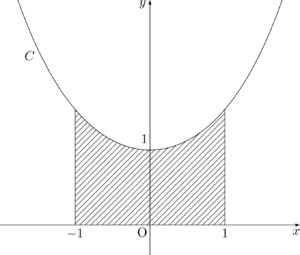
よって,求める面積 $S$ は
$S$ は図の斜線部分の面積である。

よって,求める面積 $S$ は
\begin{align*}
S&=\dint{-1}{1}\dfrac{e^x+e^{-x}}{2}\;dx \\[4pt]
&=\dint{0}{1}(e^x+e^{-x})\;dx \\[4pt]
&=\tint{e^x-e^{-x}}{0}{1} \\[4pt]
&=e-\dfrac{1}{e}
\end{align*}
S&=\dint{-1}{1}\dfrac{e^x+e^{-x}}{2}\;dx \\[4pt]
&=\dint{0}{1}(e^x+e^{-x})\;dx \\[4pt]
&=\tint{e^x-e^{-x}}{0}{1} \\[4pt]
&=e-\dfrac{1}{e}
\end{align*}

ヒロ
曲線の長さの公式を思い出して解こう。
【(4)の解答】
\begin{align*}
1+(y’)^2&=1+\left(\dfrac{e^x-e^{-x}}{2}\right)^2 \\[4pt]
&=\left(\dfrac{e^x+e^{-x}}{2}\right)^2
\end{align*}
であり,$y>0$ であるから1+(y’)^2&=1+\left(\dfrac{e^x-e^{-x}}{2}\right)^2 \\[4pt]
&=\left(\dfrac{e^x+e^{-x}}{2}\right)^2
\end{align*}
\begin{align*}
\sqrt{1+(y’)^2}=\sqrt{y^2}=y
\end{align*}
よって,求める長さ $L$ は\sqrt{1+(y’)^2}=\sqrt{y^2}=y
\end{align*}
\begin{align*}
L&=\dint{-1}{1}\sqrt{1+(y’)^2}\;dx \\[4pt]
&=\dint{-1}{1}y\;dx \\[4pt]
&=e-\dfrac{1}{e}
\end{align*}
L&=\dint{-1}{1}\sqrt{1+(y’)^2}\;dx \\[4pt]
&=\dint{-1}{1}y\;dx \\[4pt]
&=e-\dfrac{1}{e}
\end{align*}

ヒロ
(4)の積分は面積を求める式と同じになったから,結果を再利用しよう。
まとめ

ヒロ
カテナリー曲線(懸垂線)についてまとめると次のようになる。
カテナリー曲線
- グラフの概形

- 方程式\begin{align*}
y=\dfrac{a(e^{\frac{x}{a}}+e^{-\frac{x}{a}})}{2}
\end{align*} - 曲線の長さに利用できる等式\begin{align*}
\sqrt{1+\{f'(x)\}^2}=\dfrac{f(x)}{a}
\end{align*} - 面積に利用できる等式\begin{align*}
\dint{}{}f(x)\;dx=a^2f'(x)+C
\end{align*}