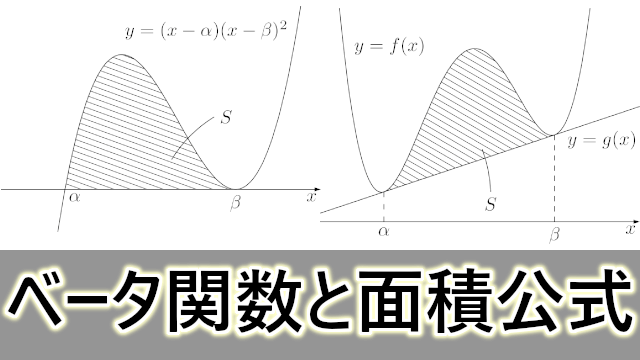
面積公式である6分の1公式や12分の1公式については，もう使えるようになっているだろうか？定積分で表された式を見て，結論の式がすぐに出てくるだろうか？
どうなるんだっけ？となる人は，ベータ関数について学習することで，6分の1公式や12分の1公式などの面積公式を簡単なものに感じるだろう。ただし，数学IIIを必要としない文系の人にとっては，少しオーバーワークになるような気がする。
ベータ関数とは
ヒロ
wikipediaによると，ベータ関数は次のように定義されている。
ベータ関数とは，ルジャンドルの定義に従って第一種オイラー積分とも呼ばれる特殊関数である。
wikipediaより引用
$x>0,~y>0$ のとき
\begin{align*}
B(x,~y)=\dint{0}{1}t^{x-1}(1-t)^{y-1}\;dt
\end{align*}
と定義される関数をベータ関数と呼ぶ。B(x,~y)=\dint{0}{1}t^{x-1}(1-t)^{y-1}\;dt
\end{align*}
ベータ関数に関する入試問題【2019年 兵庫県立大】
2019年 兵庫県立大任意の実数 $a,~b$ および0以上の任意の整数 $m,~n$ に対して，
(1) 関数 $f(x),~g(x)$ は微分可能で，$f(a)=0$ および $g(b)=0$ を満たすとする。このとき，次の等式が成り立つことを示せ。
\begin{align*}
A(m,~n)=\dint{a}{b}(x-a)^m(x-b)^n\;dx
\end{align*}
と定義する。次の問に答えよ。A(m,~n)=\dint{a}{b}(x-a)^m(x-b)^n\;dx
\end{align*}
(1) 関数 $f(x),~g(x)$ は微分可能で，$f(a)=0$ および $g(b)=0$ を満たすとする。このとき，次の等式が成り立つことを示せ。
\begin{align*}
\dint{a}{b}f'(x)g(x)\;dx+\dint{a}{b}f(x)g'(x)\;dx=0
\end{align*}
(2) 次の式を値を求めよ。\dint{a}{b}f'(x)g(x)\;dx+\dint{a}{b}f(x)g'(x)\;dx=0
\end{align*}
\begin{align*}
(m+1)A(m,~n+1)+(n+1)A(m+1,~n)
\end{align*}
(3) $A(m,~n)$ について次が成り立つことを示せ。(m+1)A(m,~n+1)+(n+1)A(m+1,~n)
\end{align*}
\begin{align*}
A(m,~n)=(-1)^n\dfrac{m!\,n!}{(m+n+1)!}(b-a)^{m+n+1}
\end{align*}
A(m,~n)=(-1)^n\dfrac{m!\,n!}{(m+n+1)!}(b-a)^{m+n+1}
\end{align*}
ヒロ
$f'(x)$ が $f(x)$ に，$g(x)$ が $g'(x)$ になっているから部分積分でやってみよう。
【(1)の解答】
\begin{align*}
\dint{a}{b}f'(x)g(x)\;dx&=\tint{f(x)g(x)}{a}{b}-\dint{a}{b}f(x)g'(x)\;dx \\[4pt]
&=f(b)g(b)-f(a)g(a)-\dint{a}{b}f(x)g'(x)\;dx
\end{align*}
ここで $f(a)=0,~g(b)=0$ より\dint{a}{b}f'(x)g(x)\;dx&=\tint{f(x)g(x)}{a}{b}-\dint{a}{b}f(x)g'(x)\;dx \\[4pt]
&=f(b)g(b)-f(a)g(a)-\dint{a}{b}f(x)g'(x)\;dx
\end{align*}
\begin{align*}
&\dint{a}{b}f'(x)g(x)\;dx=-\dint{a}{b}f(x)g'(x)\;dx \\[4pt]
&\dint{a}{b}f'(x)g(x)\;dx+\dint{a}{b}f(x)g'(x)\;dx=0
\end{align*}
&\dint{a}{b}f'(x)g(x)\;dx=-\dint{a}{b}f(x)g'(x)\;dx \\[4pt]
&\dint{a}{b}f'(x)g(x)\;dx+\dint{a}{b}f(x)g'(x)\;dx=0
\end{align*}
ヒロ
式の形から(1)を利用するんだろうなって思えるようにしよう。$f(x)$ と $g(x)$ をどう設定するのかが重要になるね。
【(2)の解答】
$f(x)=(x-a)^{m+1}$, $g(x)=(x-b)^{n+1}$ とすると，$f(x),~g(x)$ は微分可能で，$f(a)=0,~g(b)=0$ を満たすから(1)の等式が成り立つ。ここで
$f(x)=(x-a)^{m+1}$, $g(x)=(x-b)^{n+1}$ とすると，$f(x),~g(x)$ は微分可能で，$f(a)=0,~g(b)=0$ を満たすから(1)の等式が成り立つ。ここで
\begin{align*}
\dint{a}{b}f'(x)g(x)\;dx&=\dint{a}{b}(m+1)(x-a)^m(x-b)^{n+1}\;dx \\[4pt]
&=(m+1)A(m,~n+1) \\[4pt]
\dint{a}{b}f(x)g'(x)\;dx&=\dint{a}{b}(n+1)(x-a)^{m+1}(x-b)^n\;dx \\[4pt]
&=(n+1)A(m+1,~n)
\end{align*}
であるから\dint{a}{b}f'(x)g(x)\;dx&=\dint{a}{b}(m+1)(x-a)^m(x-b)^{n+1}\;dx \\[4pt]
&=(m+1)A(m,~n+1) \\[4pt]
\dint{a}{b}f(x)g'(x)\;dx&=\dint{a}{b}(n+1)(x-a)^{m+1}(x-b)^n\;dx \\[4pt]
&=(n+1)A(m+1,~n)
\end{align*}
\begin{align*}
(m+1)A(m,~n+1)+(n+1)A(m+1,~n)=0
\end{align*}
(m+1)A(m,~n+1)+(n+1)A(m+1,~n)=0
\end{align*}
ヒロ
誘導がなければ次のようにすれば良い。
【(2)の別解】
\begin{align*}
A(m,~n+1)&=\dint{a}{b}(x-a)^m(x-b)^{n+1}\;dx \\[4pt]
&=\Tint{\dfrac{(x-a)^{m+1}}{m+1}(x-b)^{n+1}}{a}{b}-\dint{a}{b}\dfrac{(x-a)^{m+1}}{m+1}\Cdota(n+1)(x-b)^n\;dx \\[4pt]
&=-\dfrac{n+1}{m+1}\dint{a}{b}(x-a)^{m+1}(x-b)^n\;dx \\[4pt]
&=-\dfrac{n+1}{m+1}A(m+1,~n)
\end{align*}
よってA(m,~n+1)&=\dint{a}{b}(x-a)^m(x-b)^{n+1}\;dx \\[4pt]
&=\Tint{\dfrac{(x-a)^{m+1}}{m+1}(x-b)^{n+1}}{a}{b}-\dint{a}{b}\dfrac{(x-a)^{m+1}}{m+1}\Cdota(n+1)(x-b)^n\;dx \\[4pt]
&=-\dfrac{n+1}{m+1}\dint{a}{b}(x-a)^{m+1}(x-b)^n\;dx \\[4pt]
&=-\dfrac{n+1}{m+1}A(m+1,~n)
\end{align*}
\begin{align*}
(m+1)A(m,~n+1)+(n+1)A(m+1,~n)=0
\end{align*}
(m+1)A(m,~n+1)+(n+1)A(m+1,~n)=0
\end{align*}
ヒロ
(3)は(2)の式を利用しよう。
【(3)の解答】
(2)の結果より
(2)の結果より
\begin{align*}
A(m,~n+1)=-\dfrac{n+1}{m+1}A(m+1,~n)
\end{align*}
となるから，$n\geqq1$ のときA(m,~n+1)=-\dfrac{n+1}{m+1}A(m+1,~n)
\end{align*}
\begin{align*}
A(m,~n)=-\dfrac{n}{m+1}A(m+1,~n-1)
\end{align*}
A(m,~n)=-\dfrac{n}{m+1}A(m+1,~n-1)
\end{align*}
ヒロ
あとはこれを繰り返して使っていこう。
まず，この式で1回変形すると $-1$ 倍される。$A(m,~n)$ の括弧内の左側は1増加し，右側は1減少する。係数として，$A(m,~n)$ の括弧内の左側は1増加して，右側の $n$ はそのままで分数にして前に出す。
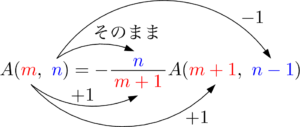
$A(m,~n)$ の左側は1増加し，右側は1減少するから，和は常に $m+n$ である。
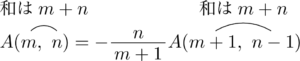
つまり，最後は $A(m+n,~0)$ となることが分かるから，そのときの係数を考える。
【解答の続き】
\begin{align*}
A(m,~n)&=-\dfrac{n}{m+1}A(m+1,~n-1) \\[4pt]
&=(-1)^2\dfrac{n(n-1)}{(m+2)(m+1)}A(m+2,~n-2) \\[4pt]
&=(-1)^3\dfrac{n(n-1)(n-2)}{(m+3)(m+2)(m+1)}A(m+3,~n-3) \\[4pt]
&=\cdots\cdots \\[4pt]
&=(-1)^{n+1}\dfrac{n(n-1)\cdots1}{(m+n)(m+n-1)\cdots(m+1)}A(m+n,~0) \\[4pt]
&=(-1)^{n+1}\dfrac{m!\,n!}{(m+n)!}A(m+n+1,~0)
\end{align*}
ここでA(m,~n)&=-\dfrac{n}{m+1}A(m+1,~n-1) \\[4pt]
&=(-1)^2\dfrac{n(n-1)}{(m+2)(m+1)}A(m+2,~n-2) \\[4pt]
&=(-1)^3\dfrac{n(n-1)(n-2)}{(m+3)(m+2)(m+1)}A(m+3,~n-3) \\[4pt]
&=\cdots\cdots \\[4pt]
&=(-1)^{n+1}\dfrac{n(n-1)\cdots1}{(m+n)(m+n-1)\cdots(m+1)}A(m+n,~0) \\[4pt]
&=(-1)^{n+1}\dfrac{m!\,n!}{(m+n)!}A(m+n+1,~0)
\end{align*}
\begin{align*}
A(m+n,~0)&=\dint{a}{b}(x-a)^{m+n}\;dx \\[4pt]
&=\Tint{\dfrac{(x-a)^{m+n+1}}{m+n+1}}{a}{b} \\[4pt]
&=\dfrac{(b-a)^{m+n+1}}{m+n+1}
\end{align*}
よって，A(m+n,~0)&=\dint{a}{b}(x-a)^{m+n}\;dx \\[4pt]
&=\Tint{\dfrac{(x-a)^{m+n+1}}{m+n+1}}{a}{b} \\[4pt]
&=\dfrac{(b-a)^{m+n+1}}{m+n+1}
\end{align*}
\begin{align*}
A(m,~n)=(-1)^n\dfrac{m!\,n!}{(m+n+1)!}(b-a)^{m+n+1}
\end{align*}
これは $n=0$ のときも成り立つ。A(m,~n)=(-1)^n\dfrac{m!\,n!}{(m+n+1)!}(b-a)^{m+n+1}
\end{align*}
ベータ関数を利用して面積公式（1/6公式・1/12公式など）を導出する
ヒロ
面積を求める公式として，6分の1公式・12分の1公式があるが，個人的には次のようにベータ関数の公式を覚えてしまっている。
次の式をいつでも導出できるようにしよう。
\begin{align*}
\dint{\alpha}{\beta}(x-\alpha)^m(\beta-x)^n\;dx=\dfrac{m!\,n!}{(m+n+1)!}(\beta-\alpha)^{m+n+1}
\end{align*}
\dint{\alpha}{\beta}(x-\alpha)^m(\beta-x)^n\;dx=\dfrac{m!\,n!}{(m+n+1)!}(\beta-\alpha)^{m+n+1}
\end{align*}
ヒロ
まずは6分の1公式から導出しよう。
【6分の1公式の導出】
$m=1,~n=1$ とすると
$m=1,~n=1$ とすると
\begin{align*}
\dint{\alpha}{\beta}(x-\alpha)(\beta-x)\;dx&=\dfrac{1!\,1!}{3!}(\beta-\alpha)^3 \\[4pt]
&=\dfrac{1}{6}(\beta-\alpha)^3
\end{align*}
\dint{\alpha}{\beta}(x-\alpha)(\beta-x)\;dx&=\dfrac{1!\,1!}{3!}(\beta-\alpha)^3 \\[4pt]
&=\dfrac{1}{6}(\beta-\alpha)^3
\end{align*}
ヒロ
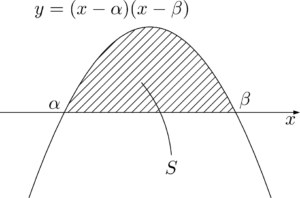
次は12分の1公式を導出しよう。
【12分の1公式の導出】
$m=1,~n=2$ とすると
$m=1,~n=2$ とすると
\begin{align*}
\dint{\alpha}{\beta}(x-\alpha)(\beta-x)^2\;dx&=\dfrac{1!\,2!}{4!}(\beta-\alpha)^4 \\[4pt]
&=\dfrac{1}{12}(\beta-\alpha)^4
\end{align*}
\dint{\alpha}{\beta}(x-\alpha)(\beta-x)^2\;dx&=\dfrac{1!\,2!}{4!}(\beta-\alpha)^4 \\[4pt]
&=\dfrac{1}{12}(\beta-\alpha)^4
\end{align*}
ヒロ
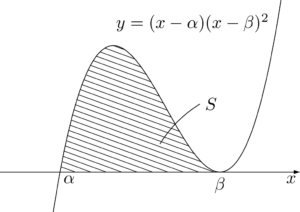
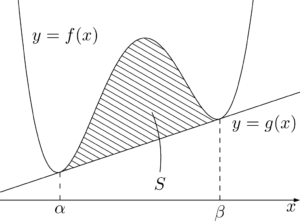
また，4次関数のグラフと二重接線（複接線）で囲まれる図形の面積は，$m=2,~n=2$ とすれば求めることができる。これは30分の1公式と呼ばれる。
【30分の1公式の導出】
$m=2,~n=2$ とすると
$m=2,~n=2$ とすると
\begin{align*}
\dint{\alpha}{\beta}(x-\alpha)^2(\beta-x)^2\;dx&=\dfrac{2!\,2!}{5!}(\beta-\alpha)^5 \\[4pt]
&=\dfrac{1}{30}(\beta-\alpha)^5
\end{align*}
下図のような場合も，$f(x)$ の $x^4$ の係数が $a$ のときは\dint{\alpha}{\beta}(x-\alpha)^2(\beta-x)^2\;dx&=\dfrac{2!\,2!}{5!}(\beta-\alpha)^5 \\[4pt]
&=\dfrac{1}{30}(\beta-\alpha)^5
\end{align*}
\begin{align*}
f(x)-g(x)=a(x-\alpha)^2(x-\beta)^2
\end{align*}
と因数分解できるため，30分の1公式で面積を求めることができる。f(x)-g(x)=a(x-\alpha)^2(x-\beta)^2
\end{align*}
まとめ
ヒロ
$\dint{\alpha}{\beta}(x-\alpha)^m(\beta-x)^n\;dx$ を部分積分することで，$\dfrac{m!\,n!}{(m+n+1)!}(\beta-\alpha)^{m+n+1}$ となる計算を定期的に何度もすることで，入試に出題されたとしても困ることはなくなるだろう。
ヒロ
また，6分の1公式や12分の1公式もより強固なものになるだろう。
