2020年センター試験 数学ⅠA 第1問 命題の解説をします。
まだ問題を解いていない人は解いてから解説を読んでください。
2020年 センターⅠA 第1問 命題〔2〕自然数 $n$ に関する三つの条件 $p,~q,~r$ を次のように定める。
$p:n$ は4の倍数である。
$q:n$ は6の倍数である。
$r:n$ は24の倍数である。
条件 $p,~q,~r$ の否定をそれぞれ $\overline{p},~\overline{q},~\overline{r}$ で表す。
条件 $p$ を満たす自然数全体の集合を $P$ とし,条件 $q$ を満たす自然数全体の集合を $Q$ とし,条件 $r$ を満たす自然数全体の集合を $R$ とする。
自然数全体の集合を全体集合とし,集合 $P,~Q,~R$ の補集合をそれぞれ
$\overline{P},~\overline{Q},~\overline{R}$ で表す。
(1) 次の $\myBox{ス}$ に当てはまるものを,下の⓪~⑤のうちから一つ選べ。
③ $\overline{P}\cap Q$ ④ $\overline{P}\cap\overline{Q}\cap R$ ⑤ $\overline{P}\cap\overline{Q}\cap\overline{R}$
(2) 次の $\mybox{タ}$ に当てはまるものを,下の⓪~④のうちから一つ選べ。
$P\cap Q$ に属する自然数のうち最小のものは $\myBox{セソ}$ である。また,$\mybox{セソ}~\myBox{タ}~R$ である。
⓪ $=$ ① $\subset$ ② $\supset$ ③ $\in$ ④ $\notin$
(3) 次の $\mybox{チ}$ に当てはまるものを,下の⓪~③のうちから一つ選べ。
自然数 $\mybox{セソ}$ は,命題 $\myBox{チ}$ の反例である。
⓪ 「$(p~かつ~q)\Rightarrow\overline{r}$」
① 「$(p~または~q)\Rightarrow\overline{r}$」
② 「$r\Rightarrow(p~かつ~q)$」
③ 「$(p~かつ~q)\Rightarrow r$」
$p:n$ は4の倍数である。
$q:n$ は6の倍数である。
$r:n$ は24の倍数である。
条件 $p,~q,~r$ の否定をそれぞれ $\overline{p},~\overline{q},~\overline{r}$ で表す。
条件 $p$ を満たす自然数全体の集合を $P$ とし,条件 $q$ を満たす自然数全体の集合を $Q$ とし,条件 $r$ を満たす自然数全体の集合を $R$ とする。
自然数全体の集合を全体集合とし,集合 $P,~Q,~R$ の補集合をそれぞれ
$\overline{P},~\overline{Q},~\overline{R}$ で表す。
(1) 次の $\myBox{ス}$ に当てはまるものを,下の⓪~⑤のうちから一つ選べ。
\begin{align*}
32\in\myBox{ス}~である。
\end{align*}
⓪ $P\cap Q\cap R$ ① $P\cap Q\cap\overline{R}$ ② $P\cap\overline{Q}$32\in\myBox{ス}~である。
\end{align*}
③ $\overline{P}\cap Q$ ④ $\overline{P}\cap\overline{Q}\cap R$ ⑤ $\overline{P}\cap\overline{Q}\cap\overline{R}$
(2) 次の $\mybox{タ}$ に当てはまるものを,下の⓪~④のうちから一つ選べ。
$P\cap Q$ に属する自然数のうち最小のものは $\myBox{セソ}$ である。また,$\mybox{セソ}~\myBox{タ}~R$ である。
⓪ $=$ ① $\subset$ ② $\supset$ ③ $\in$ ④ $\notin$
(3) 次の $\mybox{チ}$ に当てはまるものを,下の⓪~③のうちから一つ選べ。
自然数 $\mybox{セソ}$ は,命題 $\myBox{チ}$ の反例である。
⓪ 「$(p~かつ~q)\Rightarrow\overline{r}$」
① 「$(p~または~q)\Rightarrow\overline{r}$」
② 「$r\Rightarrow(p~かつ~q)$」
③ 「$(p~かつ~q)\Rightarrow r$」
(1)の考え方と解答

ヒロ
32がどの集合の要素であるかを考える問題。
【スの解答】
32は4の倍数であるから $P$ に含まれる。32は6の倍数ではないから $Q$ に含まれない,つまり $\overline{Q}$ に含まれる。32は24の倍数ではないから $R$ に含まれない,つまり $\overline{R}$ に含まれる。
よって,$32\in P\cap\overline{Q}\cap\overline{R}$ であるが,これは選択肢にはない。 $P\cap Q\neq\varnothing$, $P\supset R$, $Q\supset R$ であることを考えてベン図で表すと次のようになる。
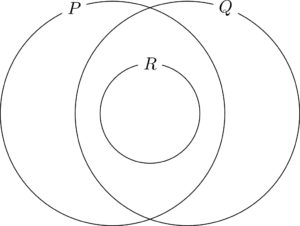
このベン図で32は下図の斜線部分内にある。
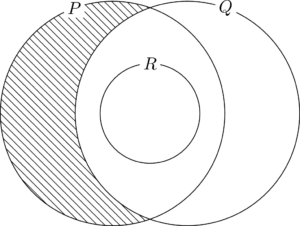
よって,$32\in P\cap\overline{Q}$ $\myBox{ス}=②$
32は4の倍数であるから $P$ に含まれる。32は6の倍数ではないから $Q$ に含まれない,つまり $\overline{Q}$ に含まれる。32は24の倍数ではないから $R$ に含まれない,つまり $\overline{R}$ に含まれる。
よって,$32\in P\cap\overline{Q}\cap\overline{R}$ であるが,これは選択肢にはない。 $P\cap Q\neq\varnothing$, $P\supset R$, $Q\supset R$ であることを考えてベン図で表すと次のようになる。

このベン図で32は下図の斜線部分内にある。

よって,$32\in P\cap\overline{Q}$ $\myBox{ス}=②$
(2)の考え方と解答
(2) 次の $\mybox{タ}$ に当てはまるものを,下の⓪~④のうちから一つ選べ。
$P\cap Q$ に属する自然数のうち最小のものは $\myBox{セソ}$ である。 また,$\mybox{セソ}~\myBox{タ}~R$ である。
⓪ $=$ ① $\subset$ ② $\supset$ ③ $\in$ ④ $\notin$

ヒロ
次は $P\cap Q$ に属する最小の自然数を求める問題。
【セ~タの解答】
$P\cap Q$ は4の倍数であり,6の倍数でもある数の集合だから,12の倍数である。よって,最小の自然数は12である。
また,12は集合 $R$ には含まれないから $12\notin R$ $\myBox{タ}=④$
$P\cap Q$ は4の倍数であり,6の倍数でもある数の集合だから,12の倍数である。よって,最小の自然数は12である。
また,12は集合 $R$ には含まれないから $12\notin R$ $\myBox{タ}=④$
(3)の考え方と解答
(3) 次の $\mybox{チ}$ に当てはまるものを,下の⓪~③のうちから一つ選べ。
自然数 $\mybox{セソ}$ は,命題 $\myBox{チ}$ の反例である。
⓪ 「$(p~かつ~q)\Rightarrow\overline{r}$」
① 「$(p~または~q)\Rightarrow\overline{r}$」
② 「$r\Rightarrow(p~かつ~q)$」
③ 「$(p~かつ~q)\Rightarrow r$」

ヒロ
12がどの命題の反例となっているかを判断する問題。
【チの解答】
まず12が属する部分をベン図で表すと下図の斜線部分のようになる。

⓪は命題を満たす例となっているので答えではない。
①も命題を満たす例となっているので答えではない。
②は $12\notin R$ より条件 $r$ を満たさず,命題は真になるから,これも答えではない。
③は $12\in P\cap Q$ であるが,$12\notin R$ であるから,12は命題③の反例である。
まず12が属する部分をベン図で表すと下図の斜線部分のようになる。

⓪は命題を満たす例となっているので答えではない。
①も命題を満たす例となっているので答えではない。
②は $12\notin R$ より条件 $r$ を満たさず,命題は真になるから,これも答えではない。
③は $12\in P\cap Q$ であるが,$12\notin R$ であるから,12は命題③の反例である。
2020年 センター数学ⅠA 命題を解いた感想

ヒロ
ベン図を描くことで楽に解けるだろう。

ヒロ
命題の真偽については,$p\Rightarrow q$ で $p$ を満たさないときは,その命題が真になることを知っておこう。




















